Введение
Постановка проблемы
В этой статье мы будем использовать GA, чтобы найти решение проблемы коммивояжера (TSP). TSP описывается следующим образом:
Для данного списка городов и расстояний между каждой парой городов, каков самый короткий маршрут, который проходит через каждый город и возвращается в исходный город?»
Иллюстрация потенциального решения TSP (Автор Xypron, из Wikimedia Commons)
Учитывая это, следует помнить о двух важных правилах:
1. Каждый город нужно посетить ровно один раз
2. Мы должны вернуться в начальный город, поэтому наше общее расстояние нужно рассчитать соответствующим образом.
Подход
Начнем с нескольких определений, перефразированных в контексте TSP:
Ген (Gene): город (в координатах (x, y))
Особь (Individual): единственный путь, удовлетворяющий указанным выше условиям
Популяция (Population): набор возможных маршрутов (т. е. совокупность особей).
Родители (Parents): два маршрута, которые объединяются для создания нового маршрута
Пул спаривания (Mating pool): набор родителей, которые используются для создания нашей следующей популяции (тем самым создавая следующее поколение маршрутов).
Функция приспособленности (Fitness): функция, которая сообщает нам, насколько хорош каждый маршрут (в нашем случае, насколько короткое расстояние)
Мутация (Mutation): способ внести разнообразие в нашу популяцию путем случайной смены местами двух городов на маршруте.
Элитарность (Elitism): способ передать лучших особей следующему поколению.
Наш GA работает следующим образом:
1. Создаем популяцию
2. Определяем функцию приспособленности.
3. Выбираем пул для спаривания.
4. Получаем потомство
5. Производим мутации
6. Повторяем.
Создание нашего генетического алгоритма
Хотя каждая часть нашего GA создается с нуля, мы будем использовать несколько стандартных пакетов, чтобы упростить задачу:
import numpy as np, random, operator, pandas as pd, matplotlib.pyplot as plt
Создание двух классов: City и Fitness.
Сначала мы создаем класс City, который позволит нам создавать и обрабатывать наши города. Это просто координаты (x, y). Внутри класса City мы добавляем расчет расстояния (используя теорему Пифагора) в строке 6 и более удобный способ вывода городов в виде координат с помощью __repr__ в строке 12.
class City:
def __init__(self, x, y):
self.x = x
self.y = y
def distance(self, city):
xDis = abs(self.x - city.x)
yDis = abs(self.y - city.y)
distance = np.sqrt((xDis ** 2) + (yDis ** 2))
return distance
def __repr__(self):
return "(" + str(self.x) + "," + str(self.y) + ")"
Также создадим класс Fitness. В нашем случае мы будем рассматривать пригодность (fitness) как обратную величину к расстоянию маршрута. Мы хотим минимизировать расстояние маршрута, поэтому более высокий показатель пригодности лучше. В соответствии с Правилом № 2 нам нужно начинать и заканчивать в одном и том же месте, поэтому этот дополнительный расчет учитывается в строке 13 расчета расстояния.
class Fitness:
def __init__(self, route):
self.route = route
self.distance = 0
self.fitness= 0.0
def routeDistance(self):
if self.distance ==0:
pathDistance = 0
for i in range(0, len(self.route)):
fromCity = self.route[i]
toCity = None
if i + 1 < len(self.route):
toCity = self.route[i + 1]
else:
toCity = self.route[0]
pathDistance += fromCity.distance(toCity)
self.distance = pathDistance
return self.distance
def routeFitness(self):
if self.fitness == 0:
self.fitness = 1 / float(self.routeDistance())
return self.fitness
Создание популяции
Теперь мы можем создать нашу первоначальную популяцию (также известную как первое поколение). Для этого нам нужен способ создания функции, которая создает маршруты, удовлетворяющие нашим условиям (примечание: мы создадим наш список городов, когда фактически запустим GA в конце статьи). Чтобы создать особь, мы случайным образом выбираем порядок посещения каждого города:
def createRoute(cityList):
route = random.sample(cityList, len(cityList))
return route
В результате получается одна особь, но нам нужна полная популяция, поэтому давайте сделаем это в нашей следующей функции. Это просто вызовы функции createRoute, пока у нас не будет столько маршрутов, сколько мы хотим для нашей популяции.
def initialPopulation(popSize, cityList):
population = []
for i in range(0, popSize):
population.append(createRoute(cityList))
return population
Примечание: мы должны использовать эти функции только для создания начальной популяции. Последующие поколения будут производиться путем размножения и мутаций.
Задаем пригодность
Далее начинается эволюционное веселье. Чтобы смоделировать наше «выживание наиболее приспособленных», мы можем использовать Fitness для ранжирования каждой особи в популяции. Нашими выходными данными будет упорядоченный список с идентификаторами маршрутов и связанной оценкой пригодности.
def rankRoutes(population):
fitnessResults = {}
for i in range(0,len(population)):
fitnessResults[i] = Fitness(population[i]).routeFitness()
return sorted(fitnessResults.items(), key = operator.itemgetter(1), reverse = True)
Выбор пула спаривания
Есть несколько вариантов выбора родителей, которые будут использоваться для создания следующего поколения. Наиболее распространенные подходы - это пропорциональный отбор по пригодности (он же «выбор колеса рулетки») или турнирный отбор:
Fitness proportionate selection (версия, реализованная ниже): для определения вероятности выбора используется приспособленность каждого человека по отношению к генеральной совокупности. Думайте об этом как о взвешенной по пригодности вероятности быть выбранным.
Tournament selection: определенное количество особей случайным образом выбирается из популяции, и тот, у кого самая высокая физическая подготовка в группе, выбирается в качестве первого родителя. Это повторяется для выбора второго родителя.
Еще одна особенность дизайна, которую следует учитывать, - это использование элитарности. При элитарности наиболее успешные особи из популяции автоматически переходят к следующему поколению, обеспечивая сохранение наиболее успешных особей.
Для большей ясности мы создадим пул спаривания в два этапа. Во-первых, мы воспользуемся выходными данными rankRoutes, чтобы определить, какие маршруты выбрать в нашей функции selection. В строках 3–5 мы настраиваем колесо рулетки, вычисляя относительный вес физической формы для каждой особи. В строке 9 мы сравниваем случайно выпавшее число с этими весами, чтобы выбрать наш пул спаривания. Мы также хотим придерживаться наших лучших маршрутов, поэтому мы вводим элитарность в строке 7. В конечном итоге функция выбора возвращает список идентификаторов маршрутов, который мы можем использовать для создания пула спаривания в функции matingPool.
def selection(popRanked, eliteSize):
selectionResults = []
df = pd.DataFrame(np.array(popRanked), columns=["Index","Fitness"])
df['cum_sum'] = df.Fitness.cumsum()
df['cum_perc'] = 100*df.cum_sum/df.Fitness.sum()
for i in range(0, eliteSize):
selectionResults.append(popRanked[i][0])
for i in range(0, len(popRanked) - eliteSize):
pick = 100*random.random()
for i in range(0, len(popRanked)):
if pick <= df.iat[i,3]:
selectionResults.append(popRanked[i][0])
break
return selectionResults
Теперь, когда у нас есть идентификаторы маршрутов, которые будут составлять наш пул спаривания из функции selection, мы можем создать пул спаривания. Мы просто извлекаем выбранных особей из нашей популяции.
def matingPool(population, selectionResults):
matingpool = []
for i in range(0, len(selectionResults)):
index = selectionResults[i]
matingpool.append(population[index])
return matingpool
Размножение
Создав наш пул спаривания, мы можем создать следующее поколение в процессе, называемом crossover (также известным как «размножение»). Если бы наши особи были строками из нулей и единиц, и наши два правила не применялись (например, представьте, что мы решаем, включать ли акции в портфель), мы могли бы просто выбрать точку пересечения и соединить две строки вместе, чтобы произвести потомство.
Однако TSP уникален тем, что нам нужно включить все местоположения ровно один раз. Чтобы соблюдать это правило, мы можем использовать специальную функцию breeding, называемую упорядоченным кроссовером. В упорядоченном кроссовере мы случайным образом выбираем подмножество первой родительской строки (см. строку 12 в функции breed ниже), а затем заполняем оставшуюся часть маршрута генами от второго родителя в том порядке, в котором они появляются, без дублирования каких-либо генов в выбранном подмножестве от первого родителя (см. строку 15 в функции breed ниже).
def breed(parent1, parent2):
child = []
childP1 = []
childP2 = []
geneA = int(random.random() * len(parent1))
geneB = int(random.random() * len(parent1))
startGene = min(geneA, geneB)
endGene = max(geneA, geneB)
for i in range(startGene, endGene):
childP1.append(parent1[i])
childP2 = [item for item in parent2 if item not in childP1]
child = childP1 + childP2
return child
Затем мы обобщим это и создадим нашу дочернюю популяцию. В строке 5 мы используем элитарность, чтобы сохранить лучшие маршруты от текущей популяции. Затем в строке 8 мы используем функцию breed, чтобы заполнить оставшуюся часть следующего поколения.
def breedPopulation(matingpool, eliteSize):
children = []
length = len(matingpool) - eliteSize
pool = random.sample(matingpool, len(matingpool))
for i in range(0,eliteSize):
children.append(matingpool[i])
for i in range(0, length):
child = breed(pool[i], pool[len(matingpool)-i-1])
children.append(child)
return children
Мутации
Мутация выполняет важную функцию в GA, поскольку помогает избежать локальной конвергенции путем введения новых маршрутов, которые позволят нам исследовать другие части пространства решений. Подобно кроссоверу, TSP уделяет особое внимание мутации. Опять же, если бы у нас была хромосома из 0 и 1, мутация просто означала бы присвоение низкой вероятности изменения гена с 0 на 1 или наоборот.
Однако, поскольку мы должны соблюдать наши правила, мы не можем отбрасывать города. Вместо этого мы воспользуемся перестановкой. Это означает, что с указанной низкой вероятностью два города поменяются местами на нашем маршруте. Мы сделаем это для одной особи в нашей функции mutate:
def mutate(individual, mutationRate):
for swapped in range(len(individual)):
if(random.random() < mutationRate):
swapWith = int(random.random() * len(individual))
city1 = individual[swapped]
city2 = individual[swapWith]
individual[swapped] = city2
individual[swapWith] = city1
return individual
Затем мы можем расширить функцию mutate для работы с новой популяцией.
def mutatePopulation(population, mutationRate):
mutatedPop = []
for ind in range(0, len(population)):
mutatedInd = mutate(population[ind], mutationRate)
mutatedPop.append(mutatedInd)
return mutatedPop
Повторение
Мы почти на месте. Давайте соберем все эти части вместе, чтобы создать функцию, которая порождает новое поколение. Сначала мы ранжируем маршруты в текущем поколении с помощью rankRoutes. Затем мы определяем наших потенциальных родителей, запустив функцию selection, которая позволяет нам создать пул спаривания с помощью функции matingPool. Наконец, мы затем создаем наше новое поколение, используя функцию blendPopulation, а затем применяем мутацию с помощью функции mutatePopulation.
def nextGeneration(currentGen, eliteSize, mutationRate):
popRanked = rankRoutes(currentGen)
selectionResults = selection(popRanked, eliteSize)
matingpool = matingPool(currentGen, selectionResults)
children = breedPopulation(matingpool, eliteSize)
nextGeneration = mutatePopulation(children, mutationRate)
return nextGeneration
Эволюция в действии
Наконец-то у нас есть все необходимое для создания нашего GA! Все, что нам нужно сделать, это создать начальную популяцию, а затем мы можем перебрать столько поколений, сколько захотим. Конечно, мы также хотим увидеть лучший маршрут и то, насколько мы улучшились, поэтому мы фиксируем начальное расстояние в строке 3 (помните, расстояние является обратной величиной пригодности), конечное расстояние в строке 8 и лучший маршрут в строке 9.
def geneticAlgorithm(population, popSize, eliteSize, mutationRate, generations):
pop = initialPopulation(popSize, population)
print("Initial distance: " + str(1 / rankRoutes(pop)[0][1]))
for i in range(0, generations):
pop = nextGeneration(pop, eliteSize, mutationRate)
print("Final distance: " + str(1 / rankRoutes(pop)[0][1]))
bestRouteIndex = rankRoutes(pop)[0][0]
bestRoute = pop[bestRouteIndex]
return bestRoute
Запуск генетического алгоритма
Когда все готово, TSP решается просто в два шага:
Во-первых, нам нужен список городов, между которыми можно путешествовать. Для этой демонстрации мы создадим список из 25 случайных городов (на первый взгляд небольшое количество городов, но при помощи грубой силы придется протестировать более 300 секстиллионов маршрутов!):
cityList = []
for i in range(0,25):
cityList.append(City(x=int(random.random() * 200), y=int(random.random() * 200)))
Затем запуск генетического алгоритма представляет собой одну простую строку кода. Здесь искусство встречается с наукой; вы должны увидеть, какие предположения работают лучше всего. В этом примере у нас 100 особей в каждом поколении, 20 элитных особей, частота мутаций 1% для данного гена и 500 поколений:
geneticAlgorithm(population=cityList, popSize=100, eliteSize=20, mutationRate=0.01, generations=500)
Бонусная функция: нарисуйте улучшение
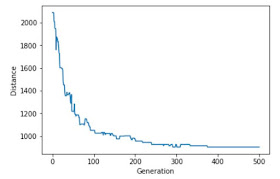
Приятно знать нашу начальную и конечную дистанцию и предлагаемый маршрут, но было бы упущением не увидеть, как со временем улучшилась наша дистанция. С помощью простой настройки нашей функции geneticAlgorithm мы можем сохранить кратчайшее расстояние от каждого поколения в списке выполнения, а затем отобразить результаты.
def geneticAlgorithmPlot(population, popSize, eliteSize, mutationRate, generations):
pop = initialPopulation(popSize, population)
progress = []
progress.append(1 / rankRoutes(pop)[0][1])
for i in range(0, generations):
pop = nextGeneration(pop, eliteSize, mutationRate)
progress.append(1 / rankRoutes(pop)[0][1])
plt.plot(progress)
plt.ylabel('Distance')
plt.xlabel('Generation')
plt.show()
Запустите GA так же, как и раньше, но теперь используя только что созданную функцию geneticAlgorithmPlot:
geneticAlgorithmPlot(population=cityList, popSize=100, eliteSize=20, mutationRate=0.01, generations=500)
Заключение
Я надеюсь, что это был забавный практический способ научиться создавать собственный GA. Попробуйте сами и посмотрите, насколько коротким маршрутом вы сможете проехать. Или пойдите дальше и попытайтсь реализовать GA на другом наборе задач.
Вы можете найти код полностью здесь.
Источники:


Can I use your code for my research project and I need yur permission. Thank you
ОтветитьУдалитьCan I use your code for my research project and I need yur permission. Thank you
ОтветитьУдалитьThis is not my code. I just translated the article.
Удалить