Оригинал: 15 TYPES OF REGRESSION IN DATA SCIENCE
Методы регрессии являются одним из самых популярных статистических методов, используемых для прогнозного моделирования и задач интеллектуального анализа данных. В среднем профессионалы аналитики знают только 2-3 типа регрессии, которые обычно используются в реальном мире. Это линейная и логистическая регрессия. Но дело в том, что существует более 10 типов регрессионных алгоритмов, разработанных для различных видов анализа. Каждый тип имеет свое назначение. Каждый аналитик должен знать, какую форму регрессии использовать в зависимости от типа данных и распределения.
Что такое регрессионный анализ?
Давайте рассмотрим простой пример: предположим, ваш менеджер попросил вас спрогнозировать годовые продажи. Там может быть сотня факторов (драйверов), которые влияют на продажи. В этом случае продажи являются вашей зависимой переменной. Факторы, влияющие на продажи, являются независимыми переменными. Регрессионный анализ поможет вам решить эту проблему.
Проще говоря, регрессионный анализ используется для моделирования отношений между зависимой переменной и одной или несколькими независимыми переменными.
Он помогает нам ответить на следующие вопросы:
- какие из драйверов оказывают существенное влияние на продажи;
- какой самый важный драйвер продаж;
- как драйверы взаимодействуют друг с другом;
- какими будут годовые продажи в следующем году.
Терминология, связанная с регрессионным анализом:
1. Выбросы
Предположим, что в наборе данных есть наблюдение, имеющее очень высокое или очень низкое значение по сравнению с другими наблюдениями в данных, то есть оно не относится к совокупности, такое наблюдение называется выбросом. Проще говоря, это экстремальное значение. Выброс - это проблема, потому что сильно влияет на полученные результаты.
2. Мультиколлинеарность
Когда независимые переменные сильно коррелируют друг с другом, переменные называются мультиколлинеарными. Многие методы регрессии предполагают, что мультиколлинеарность не должна присутствовать в наборе данных, так как это вызывает проблемы в ранжировании переменных в зависимости от их важности. Или это затрудняет работу по выбору наиболее важной независимой переменной (фактора).
3. Гетероскедастичность
Гетероскедастичность — это свойство данных, используемых при построении регрессионной модели, когда разброс точек наблюдений вдоль линии регрессии является неравномерным на всем диапазоне изменения независимой переменной. Например, по мере увеличения дохода увеличивается изменчивость потребления пищи. Бедный человек будет тратить довольно постоянную сумму, всегда есть недорогую еду. Более богатый человек может иногда покупать недорогую еду, а в другое время есть дорогую еду. Те, у кого более высокие доходы, демонстрируют большую изменчивость стоимости потребления пищи.
4. Недостаточное обучение и переобучение
Когда мы используем ненужные независимые переменные, это может привести к переобучению. Переобучение означает, что наш алгоритм хорошо работает на обучающем наборе, но не может работать лучше на тестовых наборах. Это также известно как проблема высокой дисперсии.
Когда наш алгоритм работает так плохо, что он не в состоянии соответствовать даже обучающему набору, тогда говорят, что он не соответствует данным. Это также известно как проблема высокого смещения.
На следующей диаграмме мы видим, что подгонка линейной регрессии (прямая линия на рисунке) не будет соответствовать данным, то есть это приведет к большим ошибкам даже в обучающем наборе. Использование полиномиальной регрессии на втором графике сбалансировано, т. е. такая подгонка может хорошо работать на обучающем и тестовом наборах, в то время как на третьем графике подгонка приведет к низким ошибкам в обучающем наборе, но не будет хорошо работать на тестовом наборе.
Типы регрессии
Каждый метод регрессии имеет некоторые допущения, с которыми мы должны ознакомиться, прежде чем проводить анализ. Эти методы различаются с точки зрения типа зависимых и независимых переменных и их распределения.
1. Линейная регрессия
Это самая простая форма регрессии. Это метод, в котором зависимая переменная является непрерывной по своей природе. Предполагается, что связь между зависимой и независимой переменными носит линейный характер. Мы можем наблюдать, что приведенный график представляет собой линейную зависимость между пробегом и смещением автомобилей. Зеленые точки - это фактические наблюдения, а черная линия соответствует линии регрессии.
- Когда у вас есть только 1 независимая переменная и 1 зависимая, это называется простой линейной регрессией.
- Если у вас более 1 независимой переменной и 1 зависимой, это называется множественной линейной регрессией.
Уравнение линейной регрессии приведено ниже:
Здесь «y» - это зависимая переменная, которую нужно оценить, X - независимые переменные, а ε - член ошибки. βi - это коэффициенты регрессии.
Допущения линейной регрессии:
- должна существовать линейная связь между независимыми и зависимыми переменными;
- не должно быть никаких выбросов;
- нет гетероскедастичности;
- наблюдения должны быть независимыми;
- ошибки должны быть нормально распределены со средним значением 0 и постоянной дисперсией;
- отсутствие мультиколлинеарности и автокорреляции.
Оценка параметров
Для оценки коэффициентов регрессии βi мы используем принцип наименьших квадратов, который заключается в минимизации суммы квадратов ошибок, т.е.
При решении приведенного выше уравнения получаем коэффициенты регрессии в виде:
Интерпретация коэффициентов регрессии
Давайте рассмотрим пример, где зависимая переменная - это оценки, полученные студентом, а независимые переменные - это количество часов учебы и количество посещенных занятий. Предположим, что мы получили линейную регрессию в виде:
Оценки = 5 + 2 (количество часов учебы) + 0.5(количество посещенных занятий)
Таким образом, коэффициенты регрессии имеют значения 2 и 0,5, которые можно интерпретировать как:
- если количество часов и количество посещенных занятий учебы равны нулю , то студент получит 5 баллов;
- при постоянном количестве посещаемых занятий, за каждый дополнительный час учебы студент получит еще 2 балла;
- аналогично, при постоянном количестве часов учебы, за каждое посещенное дополнительное занятие студент получит еще 0,5 балла.
Линейная регрессия в R
Рассмотрим набор данных для swiss демонстрации линейной регрессии в R. Мы используем функцию lm() в пакете base. Мы пытаемся оценить рождаемость (Fertility) с помощью других переменных.
library(datasets)
model = lm(Fertility ~ .,data = swiss)
lm_coeff = model$coefficients
lm_coeff
summary(model)
model = lm(Fertility ~ .,data = swiss)
lm_coeff = model$coefficients
lm_coeff
summary(model)
Вывод:
> lm_coeff
(Intercept) Agriculture Examination Education Catholic
66.9151817 -0.1721140 -0.2580082 -0.8709401 0.1041153
Infant.Mortality
1.0770481
> summary(model)
Call:
lm(formula = Fertility ~ ., data = swiss)
Residuals:
Min 1Q Median 3Q Max
-15.2743 -5.2617 0.5032 4.1198 15.3213
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 66.91518 10.70604 6.250 1.91e-07 ***
Agriculture -0.17211 0.07030 -2.448 0.01873 *
Examination -0.25801 0.25388 -1.016 0.31546
Education -0.87094 0.18303 -4.758 2.43e-05 ***
Catholic 0.10412 0.03526 2.953 0.00519 **
Infant.Mortality 1.07705 0.38172 2.822 0.00734 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.165 on 41 degrees of freedom
Multiple R-squared: 0.7067, Adjusted R-squared: 0.671
F-statistic: 19.76 on 5 and 41 DF, p-value: 5.594e-10
Следовательно, мы видим, что 70% вариации коэффициента рождаемости можно объяснить с помощью линейной регрессии.
2. Полиномиальная регрессия
Это метод подгонки нелинейного уравнения путем полиномиальными функциями независимой переменной.
На рисунке, приведенном ниже, вы можете видеть, что красная кривая соответствует данным лучше, чем зеленая. Следовательно, в ситуациях, когда связь между зависимой и независимой переменными кажется нелинейной, мы можем использовать модели полиномиальной регрессии.
Таким образом, многочлен степени k от одной переменной записывается в виде:
Здесь мы можем создавать новые признаки, такие как:
и подгонять линейную регрессию аналогичным образом.
В случае нескольких переменных, скажем, X1 и X2, мы можем создать третий новый признак (скажем, X3), который является произведением X1 и X2, т.е.
Предупреждение: следует иметь в виду, что создание ненужных дополнительных признаков или подгонка многочленов более высокой степени может привести к переобучению.
Полиномиальная регрессия в R:
Мы используем набор данных poly.csv для подгонки полиномиальной регрессии, где мы пытаемся оценить цены домов с учетом их площади.
Сначала мы читаем данные с помощью read.csv() и делим их на зависимую и независимую переменную
data = read.csv("poly.csv")
x = data$Area
y = data$Price
x = data$Area
y = data$Price
Чтобы сравнить результаты линейной и полиномиальной регрессии, сначала подгоним линейную регрессию:
model1 = lm(y ~x)
model1$fit
model1$coeff
model1$fit
model1$coeff
Полученные коэффициенты и прогнозные значения:
> model1$fit
1 2 3 4 5 6 7 8 9 10
169.0995 178.9081 188.7167 218.1424 223.0467 266.6949 291.7068 296.6111 316.2282 335.8454
> model1$coeff
(Intercept) x
120.05663769 0.09808581
Мы создаем dataframe, где новыми переменными являются x и x square.
new_x = cbind(x,x^2)
new_x
x
[1,] 500 250000 [2,] 600 360000 [3,] 700 490000 [4,] 1000 1000000 [5,] 1050 1102500 [6,] 1495 2235025 [7,] 1750 3062500 [8,] 1800 3240000 [9,] 2000 4000000 [10,] 2200 4840000
Теперь мы подгоняем модель к новым данным обычным методом наименьших квадратов:
model2 = lm(y~new_x)
model2$fit
model2$coeff
model2$fit
model2$coeff
Расчетные значения и коэффициенты регрессии полиномиальной регрессии:
> model2$fit
1 2 3 4 5 6 7 8 9 10
122.5388 153.9997 182.6550 251.7872 260.8543 310.6514 314.1467 312.6928 299.8631 275.8110
> model2$coeff
(Intercept) new_xx new_x
-7.684980e+01 4.689175e-01 -1.402805e-04
Используя пакет ggplot2, мы пытаемся создать график для сравнения кривых линейной и полиномиальной регрессий.
library(ggplot2)
ggplot(data = data) + geom_point(aes(x = Area,y = Price)) +
geom_line(aes(x = Area,y = model1$fit),color = "red") +
geom_line(aes(x = Area,y = model2$fit),color = "blue") +
theme(panel.background = element_blank())
ggplot(data = data) + geom_point(aes(x = Area,y = Price)) +
geom_line(aes(x = Area,y = model1$fit),color = "red") +
geom_line(aes(x = Area,y = model2$fit),color = "blue") +
theme(panel.background = element_blank())
3. Логистическая регрессия
В логистической регрессии зависимая переменная имеет бинарный характер. Независимые переменные могут быть непрерывными или бинарными.
Вот моя модель:
Почему мы не используем в этом случае линейную регрессию?
- нарушается предположение о гомоскедастичности;
- ошибки не распределены нормально;
- у соответствует биномиальному распределению и, следовательно, не является нормальным.
Примеры:
- HR-аналитика: ИТ-компании нанимают большое количество людей, но одна из проблем, с которыми они сталкиваются, заключается в том, что после принятия предложения о работе многие кандидаты отказываются. Таким образом, это приводит к перерасходу средств, поскольку им приходится повторять весь процесс снова. Теперь, когда вы получаете заявление, можете ли вы предсказать, действительно ли этот кандидат наймется в организацию (бинарный исход - Join/Not Join).
- Выборы. Предположим, что нас интересуют факторы, влияющие на то, победит ли политический кандидат на выборах. Переменная исхода (ответа) является бинарной (0/1): выиграть или проиграть. Интересующие переменные предикторы - это сумма денег, потраченная на кампанию, и количество времени, затраченного на проведение кампании.
Это прогнозирование категории зависимой переменной для заданного вектора X независимых переменных. Для логистической регрессии мы имеем:
P(Y=1) = exp(a+ BₙX)/ (1+ exp(a+ BₙX))
Таким образом, мы выбираем долю вероятности, скажем, «p», и если P (Yi = 1)> p, то мы можем сказать, что Yi принадлежит классу 1, иначе 0.
Интерпретация коэффициентов логистической регрессии (концепция отношения шансов)
Если мы возьмем экспоненту от коэффициентов, то получим отношение шансов для i-й объясняющей переменной. Предположим, что отношение шансов равно двум, тогда шансы события в 2 раза больше, чем шансы, что события не будет.
Логистическая регрессия в R:
В этом случае мы пытаемся оценить, будет ли у человека рак, в зависимости от того, курит он или нет.
Мы подгоняем логистическую регрессию с помощью функции glm() и задаем family = «binomial»
model <- glm(Lung.Cancer..Y.~Smoking..X.,data = data, family = "binomial")
Прогнозные вероятности:
#Predicted Probablities
model$fitted.values
model$fitted.values
1 2 3 4 5 6 7 8 9
0.4545455 0.4545455 0.6428571 0.6428571 0.4545455 0.4545455 0.4545455 0.4545455 0.6428571
10 11 12 13 14 15 16 17 18
0.6428571 0.4545455 0.4545455 0.6428571 0.6428571 0.6428571 0.4545455 0.6428571 0.6428571
19 20 21 22 23 24 25
0.6428571 0.4545455 0.6428571 0.6428571 0.4545455 0.6428571 0.6428571
Прогнозируем, будет ли у человека рак или нет, когда мы выберем вероятность отсечения, равную 0,5
data$prediction <- model$fitted.values>0.5
> data$prediction [1] FALSE FALSE TRUE TRUE FALSE FALSE FALSE FALSE TRUE TRUE FALSE FALSE TRUE TRUE TRUE [16] FALSE TRUE TRUE TRUE FALSE TRUE TRUE FALSE TRUE TRUE
4. Квантильная регрессия
Квантильная регрессия является продолжением линейной регрессии, и мы обычно используем ее, когда в данных имеются выбросы, высокая асимметрия и гетероскедастичность.
При линейной регрессии мы прогнозируем среднее значение зависимой переменной для заданных независимых переменных. Поскольку среднее значение не описывает все распределение, моделирование среднего значения не является полным описанием взаимосвязи между зависимыми и независимыми переменными. Таким образом, мы можем использовать квантильную регрессию, которая предсказывает квантиль (или процентиль) для заданных независимых переменных.
Термин «квантиль» - то же, что «процентиль»
Основная идея квантильной регрессии: в квантильной регрессии мы пытаемся оценить квантиль зависимой переменной с учетом значений X. Обратите внимание, что зависимая переменная должна быть непрерывной.
Модель квантильной регрессии:
Для q-го квантиля мы имеем следующую модель регрессии:
Это похоже на модель линейной регрессии, но здесь целевая функция, которую мы хотим минимизировать:
где q - это q-й квантиль.
Если q = 0,5, т. е., если нас интересует медиана, то она становится медианной регрессией (или регрессией наименьшего абсолютного отклонения) и подставляя значение q = 0,5 в вышеприведенное уравнение, мы получаем целевую функцию в виде:
Интерпретация коэффициентов в квантильной регрессии:
Предположим, что уравнение регрессии для 25-го квантиля регрессии имеет вид:
y = 5.2333 + 700.823 x
Это означает, что на одну единицу увеличения x предполагаемое увеличение 25-го квантиля y составляет 700,823 единицы.
Преимущества квантильной над линейной регрессией
- она полезна, когда в данных присутствует гетероскедастичность;
- устойчива к выбросам;
- распределение зависимой переменной можно описать с помощью различных квантилей;
- она более полезна, чем линейная регрессия, если данные искажены.
Предупреждение об использовании квантильной регрессии!
Следует иметь в виду, что коэффициенты, которые мы получаем в квантильной регрессии для конкретного квантиля, должны значительно отличаться от тех, которые мы получаем из линейной регрессии. Если это не так, то наше использование квантильной регрессии неоправданно. Это может быть проверено путем наблюдения доверительных интервалов оценок коэффициентов регрессии, полученных из обеих регрессий.
Квантильная регрессия в R
Нам нужно установить пакет Quantreg для квантильной регрессии.
install.packages("quantreg")
library(quantreg)
library(quantreg)
Используя функцию rq, мы пытаемся предсказать оценку 25-го квантиля коэффициента рождаемости в данных Swiss. Для этого мы задаем tau = 0,25.
model1 = rq(Fertility~.,data = swiss,tau = 0.25)
summary(model1)
summary(model1)
tau: [1] 0.25
Coefficients:
coefficients lower bd upper bd
(Intercept) 76.63132 2.12518 93.99111
Agriculture -0.18242 -0.44407 0.10603
Examination -0.53411 -0.91580 0.63449
Education -0.82689 -1.25865 -0.50734
Catholic 0.06116 0.00420 0.22848
Infant.Mortality 0.69341 -0.10562 2.36095
Задавая tau = 0,5, мы запускаем медианную регрессию.
model2 = rq(Fertility~.,data = swiss,tau = 0.5)
summary(model2)
summary(model2)
tau: [1] 0.5
Coefficients:
coefficients lower bd upper bd
(Intercept) 63.49087 38.04597 87.66320
Agriculture -0.20222 -0.32091 -0.05780
Examination -0.45678 -1.04305 0.34613
Education -0.79138 -1.25182 -0.06436
Catholic 0.10385 0.01947 0.15534
Infant.Mortality 1.45550 0.87146 2.21101
Мы можем запустить квантильную регрессию для нескольких квантилей на одном графике.
model3 = rq(Fertility~.,data = swiss, tau = seq(0.05,0.95,by = 0.05))
quantplot = summary(model3)
quantplot
quantplot = summary(model3)
quantplot
Мы можем проверить, отличаются ли наши результаты квантильной регрессии от результатов линейной регрессии, используя графики:
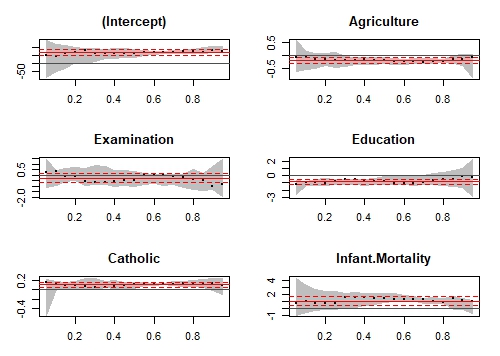
plot(quantplot)
Мы получаем следующий график:
На оси X изображены различные квантили. Красная центральная линия обозначает оценки коэффициентов линейной регрессии, а пунктирные красные линии - доверительные интервалы вокруг этих коэффициентов для различных квантилей. Черная пунктирная линия - это оценки квантильной регрессии, а серая область - доверительный интервал для них для различных квантилей. Мы можем видеть, что для всех переменных обе регрессионные оценки совпадают для большинства квантилей. Следовательно, наше использование квантильной регрессии не оправдано для таких квантилей. Другими словами, мы хотим, чтобы красная и серая линии перекрывались как можно меньше, чтобы оправдать наше использование квантильной регрессии.
5. Гребневая регрессия
Прежде, чем перейти к гребневой регрессии, важно понять концепцию регуляризации.
1. Регуляризация
Регуляризация помогает решить проблему переобучения, которая подразумевает, что модель хорошо работает с обучающими данными, но плохо работает с тестовыми данными. Регуляризация решает эту проблему, добавляя штрафной член к целевой функции и управляя сложностью модели, используя этот штрафной член.
Регуляризация обычно полезна в следующих ситуациях:
- большое количество переменных;
- низкое отношение числа наблюдений к числу переменных;
- высокая мультиколлинеарность.
2. Функция потерь L1 или регуляризация L1
В регуляризации L1 мы пытаемся минимизировать целевую функцию, добавляя штрафной член к сумме абсолютных значений коэффициентов. Этот метод также известен как метод наименьших абсолютных отклонений. Лассо-регрессия использует регуляризацию L1.
3. Функция потерь L2 или регуляризация L2
В регуляризации L2 мы пытаемся минимизировать целевую функцию, добавляя штрафной член к сумме квадратов коэффициентов. Гребневая регрессия использует регуляризацию L2.
В целом, L2 работает лучше, чем регуляризация L1. L2 эффективна с точки зрения вычислений. Есть одна область, где L1 считается предпочтительным вариантом по сравнению с L2. L1 имеет встроенный выбор признаков для разреженных пространств признаков. Например, вы прогнозируете, есть ли у человека опухоль головного мозга, используя более 20000 генетических маркеров (признаков). Известно, что подавляющее большинство генов мало или совсем не влияет на наличие или тяжесть большинства заболеваний.
В целевой функции линейной регрессии мы стараемся минимизировать сумму квадратов ошибок. В гребневой регрессии мы добавляем ограничение на сумму квадратов коэффициентов регрессии. Таким образом, в гребневой регрессии наша целевая функция:
Здесь λ - параметр регуляризации, который является неотрицательным числом. Здесь мы не предполагаем нормальность в членах ошибок.
Очень важное примечание:
Мы не регулируем intercept. Ограничение только на сумму квадратов коэффициентов регрессии X.
Мы можем видеть, что гребневая регрессия использует регуляризацию L2.
Разрешив вышеуказанную целевую функцию, мы можем получить оценки β как:
Как мы можем выбрать параметр регуляризации λ?
Если мы выберем lambda = 0, то вернемся к обычным оценкам линейной регрессии. Если лямбда выбрана очень большой, то это приведет к недостаточной подгонке. Таким образом, очень важно определить желаемое значение лямбда. Чтобы решить эту проблему, мы строим оценки параметров по различным значениям лямбды и выбираем минимальное значение λ, после которого параметры стремятся стабилизироваться.
Код R для гребневой регрессии
Взяв набор данных swiss, мы создаем два разных набора данных, один из которых содержит зависимую переменную, а другой - независимые переменные.
X = swiss[,-1]
y = swiss[,1]
y = swiss[,1]
Нам нужно загрузить библиотеку glmnet, чтобы выполнить гребневую регрессию.
library(glmnet)
Используя функцию cv.glmnet(), мы можем выполнить перекрестную проверку. По умолчанию alpha = 0, что означает, что мы выполняем гребневую регрессию. Лямбда - это последовательность различных значений лямбда, которая будет использоваться для перекрестной проверки.
set.seed(123) #Setting the seed to get similar results.
model = cv.glmnet(as.matrix(X),y,alpha = 0,lambda = 10^seq(4,-1,-0.1))
model = cv.glmnet(as.matrix(X),y,alpha = 0,lambda = 10^seq(4,-1,-0.1))
Мы берем лучшее значение лямбда, используя lambda.min, и получаем коэффициенты регрессии, используя функцию predict.
best_lambda = model$lambda.min
ridge_coeff = predict(model,s = best_lambda,type = "coefficients")
ridge_coeff
ridge_coeff = predict(model,s = best_lambda,type = "coefficients")
ridge_coeff
Коэффициенты, полученные с помощью гребневой регрессии, следующие:
6 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) 64.92994664
Agriculture -0.13619967
Examination -0.31024840
Education -0.75679979
Catholic 0.08978917
Infant.Mortality 1.09527837
6. Лассо-регрессия
Lasso расшифровывается как Absolute Shrinkage and Selection Operator. Она использует технику регуляризации L1 в целевой функции. Таким образом, целевая функция в регрессии LASSO:
λ является параметром регуляризации, а член intercept не регуляризован.
Мы не предполагаем, что ошибки распределены нормально.
Для оценок у нас нет какой-либо конкретной математической формулы, но мы можем получить оценки с помощью статистического программного обеспечения.
Обратите внимание, что лассо-регрессия также нуждается в стандартизации.
Преимущество лассо над гребневой регрессией
Лассо-регрессия может выполнять встроенный выбор признаков, а также сжатие параметров. При использовании гребневой регрессии можно получить все переменные, но с сокращенными параметрами.
Код R для лассо-регрессии
Из набора данных swiss пакета “datasets” имеем:
#Creating dependent and independent variables.
X = swiss[,-1]
y = swiss[,1]
X = swiss[,-1]
y = swiss[,1]
Используя cv.glmnet в пакете glmnet, мы выполняем перекрестную проверку. Для лассо-регрессии мы устанавливаем alpha = 1. По умолчанию standardize = TRUE, следовательно, нам не нужно стандартизировать переменные по отдельности.
#Setting the seed for reproducibility
set.seed(123)
model = cv.glmnet(as.matrix(X),y,alpha = 1,lambda = 10^seq(4,-1,-0.1))
#By default standardize = TRUE
set.seed(123)
model = cv.glmnet(as.matrix(X),y,alpha = 1,lambda = 10^seq(4,-1,-0.1))
#By default standardize = TRUE
Мы рассматриваем лучшее значение лямбда, отфильтровывая lamba.min из модели и получаем коэффициенты с помощью функции predict.
#Taking the best lambda
best_lambda = model$lambda.min
lasso_coeff = predict(model,s = best_lambda,type = "coefficients")
lasso_coeff
best_lambda = model$lambda.min
lasso_coeff = predict(model,s = best_lambda,type = "coefficients")
lasso_coeff
Полученные нами коэффициенты лассо:
6 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) 65.46374579
Agriculture -0.14994107
Examination -0.24310141
Education -0.83632674
Catholic 0.09913931
Infant.Mortality 1.07238898
Что лучше - гребневая регрессия или лассо-регрессия?
И гребневая регрессия, и лассо-регрессия предназначены для работы с мультиколлинеарностью.
Гребневая регрессия более эффективна в вычислительном отношении, чем регрессия лассо. Любая из них может работать лучше. Поэтому лучший подход - выбрать ту регрессионную модель, которая хорошо соответствует данным тестового набора.
7. Регрессия эластичной сети (Elastic Net Regression)
Регрессия эластичной сети предпочтительнее, чем гребневая и лассо-регрессия, когда мы имеем дело с сильно коррелированными независимыми переменными.
Это комбинация регуляризации L1 и L2.
Целевая функция в случае регрессии эластичной сети:
Подобно гребневой и лассо-регрессии, она не предполагает нормальности распределения ошибок.
Код R для регрессии эластичной сети
Установив другое значение alpha между 0 и 1, мы можем выполнить регрессию эластичной сети.
set.seed(123)
model = cv.glmnet(as.matrix(X),y,alpha = 0.5,lambda = 10^seq(4,-1,-0.1))
#Taking the best lambda
best_lambda = model$lambda.min
en_coeff = predict(model,s = best_lambda,type = "coefficients")
en_coeff
model = cv.glmnet(as.matrix(X),y,alpha = 0.5,lambda = 10^seq(4,-1,-0.1))
#Taking the best lambda
best_lambda = model$lambda.min
en_coeff = predict(model,s = best_lambda,type = "coefficients")
en_coeff
Полученные коэффициенты:
6 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) 65.9826227
Agriculture -0.1570948
Examination -0.2581747
Education -0.8400929
Catholic 0.0998702
Infant.Mortality 1.0775714
8. Регрессия главных компонент (PCR)
PCR - это метод регрессии, который широко используется, когда у вас есть много независимых переменных или в ваших данных присутствует мультиколлинеарность. Он делится на 2 этапа:
1. Получение главных компонент
2. Выполнение регрессионного анализа главных компонент.
Наиболее известные особенности PCR:
1. Уменьшение размерности
2. Удаление мультиколлинеарности
Получение главных компонент
Анализ главных компонент - это статистический метод для извлечения новых признаков, когда исходные признаки сильно коррелированы. Мы создаем новые признаки с помощью оригинальных признаков, так что новые признаки не коррелированы между собой.
Давайте рассмотрим первый главный компонент:
У первого главного компонента максимальная дисперсия.
Точно так же мы можем найти второй главный компонент U2, который не коррелирует с U1 и имеет вторую по величине дисперсию.
Аналогичным образом для функций «p» у нас может быть максимум «p» главных компонент, так что все главные компоненты не коррелируют друг с другом, и первый главный компонент имеет максимальную дисперсию, затем второй главный компонент имеет максимальную дисперсию и так далее.
Недостатки:
Следует отметить, что PCR - это не метод выбора признаков, а метод извлечения признаков. Каждый основной компонент, который мы получаем, является функцией всех признаков. Следовательно, используя главные компоненты, невозможно объяснить, какой фактор в какой степени влияет на зависимую переменную.
Регрессия главных компонент в R
Мы используем набор данных longley, доступный в R, который используется для моделирования высокой мультиколлинеарности. Мы исключаем столбец Year.
data1 = longley[,colnames(longley) != "Year"]
View(data)
Вот как будут выглядеть некоторые наблюдения в нашем наборе данных:
Мы используем пакет PLS для запуска PCR.
install.packages("pls")
library(pls)
library(pls)
В PCR мы пытаемся оценить количество Employed; scale = T означает, что мы стандартизируем переменные; validation = «CV» обозначает применимость перекрестной проверки.
pcr_model <- pcr(Employed~., data = data1, scale = TRUE, validation = "CV")
summary(pcr_model)
summary(pcr_model)
Получаем следующий вывод:
Data: X dimension: 16 5
Y dimension: 16 1
Fit method: svdpc
Number of components considered: 5
VALIDATION: RMSEP
Cross-validated using 10 random segments.
(Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps
CV 3.627 1.194 1.118 0.5555 0.6514 0.5954
adjCV 3.627 1.186 1.111 0.5489 0.6381 0.5819
TRAINING: % variance explained
1 comps 2 comps 3 comps 4 comps 5 comps
X 72.19 95.70 99.68 99.98 100.00
Employed 90.42 91.89 98.32 98.33 98.74
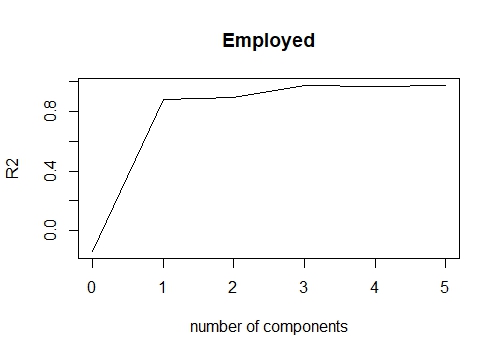
Здесь под RMSEP подразумеваются среднеквадратические ошибки. В разделе "Training: %variance explained" отображается совокупный % вариации, объясняемой главными компонентами. Мы видим, что к 3-м главным компонентам можно отнести более 99% вариации.
Мы также можем создать график, отображающий среднеквадратическую ошибку для количества различных главных компонент.
validationplot(pcr_model,val.type = "MSEP")
Написав val.type = «R2», мы можем построить R square для различных главных компонент.
validationplot(pcr_model,val.type = "R2")
Если мы хотим подогнать pcr для 3 главных компонент и, следовательно, получить предсказанные значения, мы можем написать:
pred = predict(pcr_model,data1,ncomp = 3)
9. Регрессия частичных наименьших квадратов (PLS)
Это альтернативный метод регрессии главных компонент, когда независимые переменные сильно коррелированы. Он также полезен при большом количестве независимых переменных.
Разница между PLS и PCR
Оба метода создают новые независимые переменные, называемые компонентами, которые представляют собой линейные комбинации исходных переменных-предикторов, но PCR создает компоненты для объяснения наблюдаемой изменчивости переменных-предикторов без учета зависимой переменной. В то же время PLS принимает во внимание зависимую переменную и поэтому часто приводит к моделям, которые могут соответствовать зависимой переменной, с меньшим количеством компонентов.
Регрессия частичных наименьших квадратов в R
library(plsdepot)
data(vehicles)
pls.model = plsreg1(vehicles[, c(1:12,14:16)], vehicles[, 13], comps = 3)
# R-Square
pls.model$R2
data(vehicles)
pls.model = plsreg1(vehicles[, c(1:12,14:16)], vehicles[, 13], comps = 3)
# R-Square
pls.model$R2
10. Регрессия опорных векторов (SVR)
Регрессия опорных векторов позволяет создавать как линейные, так и нелинейные модели. SVM использует нелинейные функции ядра (например полиномиальные), чтобы найти оптимальное решение для нелинейных моделей.
library(e1071)
svr.model <- svm(Y ~ X , data)
pred <- predict(svr.model, data)
points(data$X, pred, col = "red", pch=4)
svr.model <- svm(Y ~ X , data)
pred <- predict(svr.model, data)
points(data$X, pred, col = "red", pch=4)
11. Порядковая регрессия
Порядковая регрессия используется для прогнозирования ранжированных значений. Проще говоря, этот тип регрессии подходит, когда зависимая переменная имеет порядковый характер. Пример порядковых переменных - ответы на опрос (шкала от 1 до 6), реакция пациента на дозу лекарства (нет, легкая, тяжелая).
Почему мы не можем использовать линейную регрессию при работе с порядковой целевой переменной?
В линейной регрессии зависимая переменная предполагает, что изменения уровня зависимой переменной эквивалентны во всем диапазоне переменной. Например, разница в весе между человеком весом 100 кг и человеком весом 120 кг составляет 20 кг, что имеет то же значение, что и разница в весе между человеком весом 150 кг и человеком весом 170 кг. Эти отношения не обязательно верны для порядковых переменных.
library(ordinal)
o.model <- clm(rating ~ ., data = wine)
summary(o.model)
o.model <- clm(rating ~ ., data = wine)
summary(o.model)
12. Регрессия Пуассона.
Регрессия Пуассона используется, когда зависимая переменная содержит данные подсчета.
Применение регрессии Пуассона:
1. Прогнозирование количества звонков в службу поддержки клиентов, связанных с конкретным продуктом.
2. Оценка количества звонков в службу экстренной помощи во время некоторого события.
Зависимая переменная должна соответствовать следующим условиям:
1. Зависимая переменная имеет распределение Пуассона.
2. Количество не может быть отрицательным.
3. Этот метод не подходит для нецелых чисел.
В приведенном ниже коде мы используем набор данных с именем warpbreaks, который показывает количество разрывов пряжи во время плетения. В этом случае модель включает в себя термины для типа шерсти, натяжения шерсти и взаимодействия между ними.
pos.model<-glm(breaks~wool*tension, data = warpbreaks, family=poisson)
summary(pos.model)
summary(pos.model)
13. Отрицательная биномиальная регрессия.
Как и регрессия Пуассона, она также работает с данными подсчета. Возникает вопрос «чем она отличается от регрессии Пуассона?». Ответ: отрицательная биномиальная регрессия не предполагает распределения количества подсчетов, имеющего дисперсию, равную его среднему значению. Регрессия Пуассона предполагает дисперсию, равную ее среднему значению.
Когда дисперсия данных подсчета больше, чем среднее значение, это случай избыточной дисперсии. Противоположность предыдущему утверждению - случай недостаточной дисперсии.
library(MASS)
nb.model = glm.nb(Days ~ Sex/(Age + Eth*Lrn), data = quine)
summary(nb.model)
nb.model = glm.nb(Days ~ Sex/(Age + Eth*Lrn), data = quine)
summary(nb.model)
14. Квазипуассоновская регрессия.
Это альтернатива отрицательной биномиальной регрессии. Его также можно использовать для данных подсчета с большой дисперсией. Оба алгоритма дают похожие результаты, есть различия в оценке влияния ковариаций. Дисперсия квазипуассоновской модели является линейной функцией среднего, в то время как дисперсия отрицательной биномиальной модели является квадратичной функцией среднего.
qs.pos.model = glm(Days ~ Sex/(Age + Eth*Lrn), data = quine, family = "quasipoisson")
Квазипуассоновская регрессия может справиться как с избыточной, так и с недостаточной дисперсией.
15. Регрессия Кокса.
Регрессия Кокса подходит для данных о времени до события. См. примеры ниже:
1. Время с момента открытия клиентом счета до его истощения.
2. Время от начала лечения рака до смерти.
3. Время от первого сердечного приступа до второго.
Логистическая регрессия использует двоичную зависимую переменную, но игнорирует время событий.
Помимо оценки времени, необходимого для достижения определенного события, анализ выживаемости также может использоваться для сравнения времени до события для нескольких групп.
Для модели выживания установлены двойные цели:
1. Непрерывная переменная, представляющая время до события.
2. Двоичная переменная, представляющая статус, произошло событие или нет.
library(survival)
# Lung Cancer Data
# status: 2=death
lung$SurvObj = with(lung, Surv(time, status == 2))
cox.reg = coxph(SurvObj ~ age + sex + ph.karno + wt.loss, data = lung)
cox.reg
# Lung Cancer Data
# status: 2=death
lung$SurvObj = with(lung, Surv(time, status == 2))
cox.reg = coxph(SurvObj ~ age + sex + ph.karno + wt.loss, data = lung)
cox.reg
Как выбрать правильную регрессионную модель?
Если зависимая переменная является непрерывной, а модель страдает от коллинеарности или имеется много независимых переменных, вы можете попробовать PCR, PLS, гребневую регрессию, лассо и регрессию эластичной сети.
Если вы работаете с данными подсчета, вам следует попробовать пуассоновскую, квазипуассоновскую и отрицательную биномиальную регрессию.
Чтобы избежать переобучения, мы можем использовать метод перекрестной проверки для оценки моделей, используемых для прогнозирования. Мы также можем использовать методы гребневой регрессии, лассо и эластичной сетки, чтобы исправить проблему переобучения.
Попробуйте регрессию опорных векторов, если у вас нелинейная модель.





















Комментариев нет:
Отправить комментарий