Вопрос, который большинству из нас задавали в какой-то момент нашей жизни: «Какое кратчайшее расстояние между двумя точками?» По умолчанию большинство из нас дадут тот же ответ, который дал Архимед более 2000 лет назад: прямая линия. Если вы возьмете плоский лист бумаги и нанесете на него две точки в любом месте, вы можете соединить эти две точки любой линией, которую только можете вообразить. Пока бумага остается плоской, не изогнутой, прямая линия, соединяющая эти две точки, будет кратчайшим способом их соединения.
Именно так три измерения пространства работают в нашей Вселенной: в плоском пространстве кратчайшее расстояние между любыми двумя точками - это прямая линия. Это верно независимо от того, как вы вращаете, ориентируете или иным образом размещаете эти две точки. Но наша Вселенная состоит не из трех пространственных измерений, а из четырех пространственно-временных. Легко взглянуть на это и сказать: «Ну, три из них - это пространство, а одно - время, и вот здесь мы получаем пространство-время», и это правда, но не вся. В конце концов, кратчайшее расстояние между двумя пространственно-временными событиями уже не прямая линия. Вот почему.
Обычно мы измеряем расстояние между двумя точками по пройденному расстоянию, например, по линии, соединяющей точки A и B. Но самое короткое расстояние между ними - это прямая линия, напрямую соединяющая точки A и B. Это работает только для пространственных расстояний. (SIMEON87 / WIKIMEDIA COMMONS; E. SIEGEL)
Для большинства из нас наше первое знакомство с идеей прямой линии как кратчайшего расстояния между двумя точками происходит из места, которое мы, возможно, не осознаем: теорема Пифагора. Возможно, вы помните теорему Пифагора о прямоугольных треугольниках: если вы возведете в квадрат каждую из коротких сторон и сложите их вместе, то получится квадрат длинной стороны. С математической точки зрения, если короткие стороны - это a и b, а длинная сторона - это c, то уравнение, связывающее их, будет a² + b² = c².
Подумайте, однако, о том, что это означает, не только с точки зрения чистой математики, а с точки зрения расстояний. Это означает, что если вы перемещаетесь через одно из своих пространственных измерений на определенную величину (например, a), а затем перемещаетесь через перпендикулярное измерение на другую величину (например, b), тогда расстояние между тем местом, где вы начали, и местом, где вы остановились, равно c, как определено теоремой Пифагора. Другими словами, расстояние между любыми двумя точками на плоскости, где эти точки разделяет a в одном измерении и b в другом измерении, равно c, где c = √ (a² + b²).
Есть много способов визуализировать простое уравнение Пифагора, такое как a² + b² = c², но не все визуализации одинаково полезны, когда дело доходит до расширения этого уравнения различными математическими способами. (AMERICANXPLORER13 AT ENGLISH WIKIPEDIA).
В нашей Вселенной, конечно, мы не ограничены жизнью на плоском листе бумаги. У нас есть не только длина и ширина (или направления x и y, если хотите) нашей Вселенной, но и глубина (или направление z). Если вы хотите выяснить расстояние между любыми двумя точками в пространстве, это тот же метод, что и в двух измерениях, за исключением добавления одного дополнительного измерения. Независимо от того, на какую величину ваши две точки разделены в направлении x, в направлении y и z, вы можете вычислить общее расстояние между ними так же, как и раньше.
Из-за дополнительного измерения расстояние между ними (назовем его d) будет равно d = √ (x² + y² + z²). Это может показаться пугающим уравнением, но оно просто говорит о том, что расстояние между любыми двумя точками определяется прямой линией, соединяющей их: линией, которая учитывает расстояние между двумя вашими точками во всех трех измерениях: x, y и z.
Смещение между любыми двумя точками в трехмерном пространстве, такими как начало координат и точка P, показанные здесь, равно квадратному корню из суммы квадратов разностей расстояний по каждому из трех (x, y и z ) направления. (CRONHOLM144 / WIKIMEDIA COMMONS)
Один из интересных и важных выводов об этой взаимосвязи заключается в том, что абсолютно не имеет значения, как вы ориентируете визуализацию измерений x, y и z. Вы также можете:
- изменять свои координаты так, чтобы x, y и z находились в любых (взаимно перпендикулярных) направлениях, которые вам нравятся;
- поворачивать прямую, соединяющую эти две точки на любой угол в любом направлении;
Расстояние между ними вообще не изменится.
Конечно, изменятся отдельные компоненты, если вы либо повернете свою перспективу, либо повернете линию, соединяющую эти две точки, поскольку ваши определения длины, ширины и глубины будут изменяться относительно друг друга для этой линии по мере того, как происходит вращение. Но общее расстояние между этими двумя точками вообще не меняется; расстояние между этими точками остается «инвариантным», или неизменным, независимо от того, как вы их вращаете.
Как показано здесь, существует определенное расстояние между двумя объектами, составляющими «двойную планету», показанную здесь на переднем плане. Независимо от того, как вы ориентируете свою систему координат или как вы вращаете эти планеты в пространстве, расстояние между ними остается постоянным. (NASA / NORMAN W. LEE AND STEPHEN PAUL MESZAROS)
Теперь давайте рассмотрим не только пространство, но и время. Вы можете подумать: «ну, если время - это тоже просто измерение, тогда расстояние между любыми двумя точками в пространстве-времени будет работать таким же образом». Например, если мы представим измерение времени как t, вы можете подумать, что расстояние будет прямой линией, соединяющей две точки через три пространственных измерения, а также измерение времени. С математической точки зрения вы можете подумать, что уравнение разделения между любыми двумя точками будет выглядеть примерно так: d = √ (x² + y² + z² + t²).
В конце концов, это почти то же изменение, которое мы сделали, когда перешли от двух измерений к трем, за исключением того, что на этот раз мы перешли от трех измерений к четырем. Это разумный шаг, и он точно описывает, как бы выглядела реальность, если бы у нас было четыре измерения пространства, а не три.
Но у нас нет четырех измерений пространства; у нас есть три измерения пространства и одно измерение времени. И, несмотря на то, что вам подсказывала интуиция, время - это не «просто другое измерение».
Предвидение движения объектов во времени с помощью камеры - лишь одно из практических применений идеи времени как измерения. (SONY, HTTPS://WWW.YOUTUBE.COM/WATCH?V=WY8TAGFC95O)
Время как измерение отличается от пространства двумя аспектами. Первый: вы не можете сопоставить пространство (которое является мерой расстояния) и время (которое является мерой времени) без какого-либо способа преобразовать одно в другое. К счастью, одним из величайших открытий теории относительности Эйнштейна было то, что существует важная фундаментальная связь между расстоянием и временем: скорость света или, что то же самое, любой частицы, которая движется через Вселенную без массы покоя.
Скорость света в вакууме, 299 792 458 метров в секунду, говорит нам, как именно связать наше движение в пространстве с движением во времени: с помощью этой фундаментальной константы. Когда мы используем такие термины, как «один световой год» или «одна световая секунда», мы говорим о расстояниях в терминах времени: например, количество расстояния, которое свет проходит за один год (или одну секунду). Если мы хотим преобразовать «время» в расстояние, нам нужно умножить его на скорость света в вакууме.
Пример светового конуса, трехмерной поверхности всех возможных световых лучей, приходящих и исходящих из точки пространства-времени. Чем больше вы перемещаетесь в пространстве, тем меньше вы перемещаетесь во времени, и наоборот. Только вещи, содержащиеся в вашем прошлом световом конусе, могут повлиять на вас сейчас; только вещи, содержащиеся в вашем будущем световом конусе, могут быть восприняты вами в будущем. (WIKIMEDIA COMMONS USER MISSMJ)
Но второй аспект требует огромного скачка, чтобы понять то, что ускользало от величайших умов конца 19-го и начала 20-го веков. Ключевая идея заключается в том, что мы все движемся во Вселенной, в пространстве и времени одновременно. Если мы просто сидим здесь, неподвижно и совсем не движемся в пространстве, тогда мы движемся во времени с определенной скоростью, с которой все мы знакомы: одна секунда в секунду.
Однако, и это ключевой момент, чем быстрее вы движетесь в пространстве, тем медленнее вы движетесь во времени. Другие измерения совсем не такие: ваше движение через измерение x в пространстве, например, полностью не зависит от вашего движения через измерения y и z. Но ваше полное движение в пространстве, относительно любого другого наблюдателя, определяет ваше движение во времени. Чем больше вы перемещаетесь через одно из них (пространство или время), тем меньше вы перемещаетесь через другое.
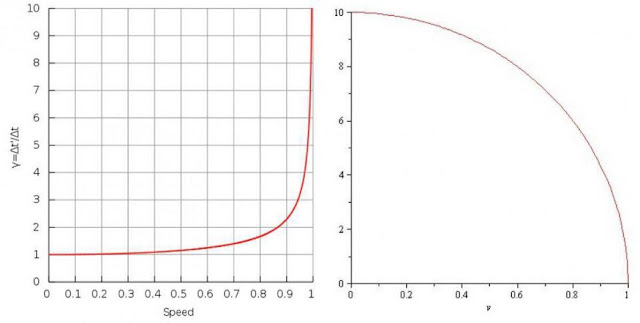
Замедление времени (L) и сокращение длины (R) показывают, как кажется, что время течет медленнее, а расстояния становятся меньше по мере приближения к скорости света. По мере приближения к скорости света время замедляется, а расстояния сокращаются до бесконечно малых величин. (WIKIMEDIA COMMONS USERS ZAYANI (L) AND JROBBINS59 (R))
Вот почему теория относительности Эйнштейна дает нам такие понятия, как замедление времени и сокращение длины. Если вы двигаетесь с очень низкой скоростью по сравнению со скоростью света, вы не заметите этих эффектов: кажется, что время движется со скоростью одну секунду в секунду для всех, а длины кажутся одинаковыми для всех на скоростях, обычно достижимых на Земле.
Но по мере того, как вы приближаетесь к скорости света, или, скорее, когда вы видите объект, относительная скорость которого между вами и ним близка к скорости света, вы заметите, что он сжимается в направлении своего относительного движения, и часы идут медленнее по сравнению с вашими собственными часами.
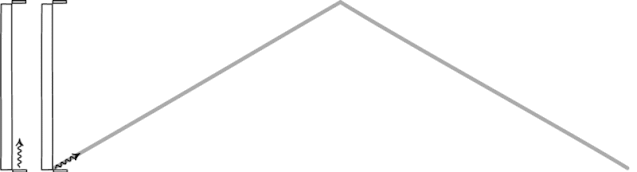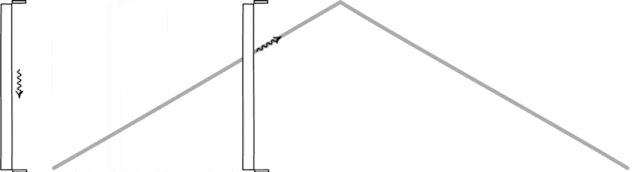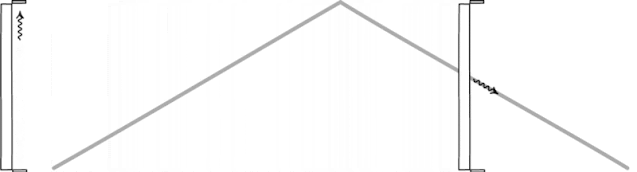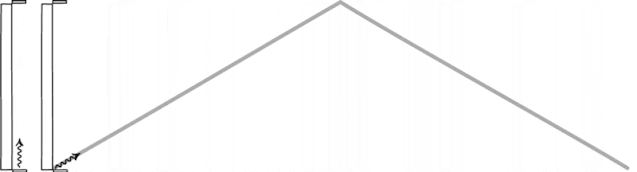
Причина, лежащая в основе этого, как понял Эйнштейн, была проста: это происходит потому, что скорость света одинакова для всех наблюдателей. Если вы представите себе, что ход часов определяется светом, отражающимся туда и обратно между двумя зеркалами, то наблюдение за чужими часами, когда они движутся со скоростью, близкой к скорости света, неизбежно приведет к тому, что их часы будут идти медленнее, чем ваши.
Световые часы, образованные фотоном, прыгающим между двумя зеркалами, будут определять время для любого наблюдателя. Хотя два наблюдателя могут не соглашаться друг с другом относительно того, сколько времени проходит, они соглашаются в законах физики и константах Вселенной, таких как скорость света. Стационарный наблюдатель увидит, что время идет нормально, но у наблюдателя, быстро движущегося в пространстве, часы будут идти медленнее, чем у неподвижного наблюдателя. (JOHN D. NORTON)
Но здесь есть еще более глубокое понимание, которое изначально ускользало даже от самого Эйнштейна. Если вы рассматриваете время как измерение, умножаете его на скорость света и (вот большой скачок) относитесь к нему как к мнимому, а не реальному, тогда мы можем определить «интервал пространства-времени» так же, как мы определили расстояние ранее. Только, поскольку мнимое число i равно √ (-1), это означает, что интервал пространства-времени фактически равен d = √ (x² + y² + z² - c²t²). [Обратите внимание на знак минус, прикрепленный к временной координате!]
Другими словами, преобразование от «движения в пространстве» к «движению во времени» также является вращением, но это вращение не в декартовых координатах пространства (где x, y и z - все действительные числа), но через гиперболические координаты пространства-времени, где, если пространственные координаты действительны, то координата времени должна быть мнимой.
По иронии судьбы, человеком, который первым сложил эти кусочки головоломки, был бывший учитель Эйнштейна Герман Минковский, который в 1907/8 году отметил, что: «Отныне пространство само по себе и время само по себе обречены исчезнуть в тенях, и только своего рода союз этих двух сохранит независимую реальность».
Благодаря математической строгости Минковского концепция пространства-времени не только родилась, но и должна была остаться.
Гиперболические координаты, нарисованные красным и синим цветом, подчиняются фундаментально отличным математическим отношениям между двумя различными наборами осей, по сравнению с традиционными декартовыми координатами (ROCCHINI / WIKIMEDIA COMMONS).
Что примечательно во всем этом, так это то, что Эйнштейн, несмотря на недостаток математического понимания, чтобы точно понять, как измерение времени связано с тремя традиционными измерениями пространства, все же смог собрать воедино это ключевое физическое открытие. Увеличение вашего движения в пространстве уменьшало ваше движение во времени, а увеличение вашего движения во времени уменьшало ваше движение в пространстве. Все измерения пространства и времени имеют смысл только по отношению к рассматриваемому наблюдателю и зависят от относительного движения наблюдателя к наблюдаемому.
И все же пространственно-временной интервал остается неизменным. Независимо от того, кто является наблюдателем, или как быстро они движутся, все наблюдатели могут согласиться с комбинированным движением любого объекта в пространстве-времени. В некотором смысле успех теории относительности стал еще более впечатляющим в свете оценки Эйнштейна Минковским. В разговоре со своим (более поздним) учеником Максом Борном Минковский сказал следующее: «Для меня [теория относительности] стала огромным сюрпризом, поскольку в студенческие годы Эйнштейн был настоящим лентяем. Он вообще никогда не интересовался математикой». К счастью, в физике сама Вселенная, а не чье-либо мнение, является окончательным арбитром научной истины.







Комментариев нет:
Отправить комментарий