Полное руководство по 12 техникам уменьшения размерности (с кодом Python)

Оригинал: The Ultimate Guide to 12 Dimensionality Reduction Techniques (with Python codes)

Введение

Вы когда-нибудь работали с набором данных, содержащим более тысячи признаков? Как насчет более 50 000 признаков? У меня они есть, и позвольте мне сказать вам, что это очень сложная задача, особенно если вы не знаете, с чего начать! Наличие большого количества переменных - это и благо, и проклятие. Здорово, что у нас есть масса данных для анализа, но это сложно из-за размера.

Невозможно проанализировать каждую переменную на микроскопическом уровне. На выполнение сколько-нибудь значимого анализа у нас могут уйти дни или месяцы, и мы потеряем кучу времени и денег! Не говоря уже о вычислительной мощности, которая для этого потребуется. Нам нужен лучший способ работы с многомерными данными, чтобы мы могли быстро извлекать из них закономерности и идеи. Итак, как нам подойти к такому набору данных?

Конечно, используя методы уменьшения размерности. Вы можете использовать эту концепцию, чтобы уменьшить количество признаков в вашем наборе данных, не теряя при этом много информации, и сохранить (или улучшить) производительность модели. Как вы увидите в этой статье, это действительно эффективный способ работы с огромными наборами данных.

Это подробное руководство по различным методам уменьшения размерности, которые можно использовать в практических сценариях. Сначала мы поймем, что это за концепция и почему мы должны ее использовать, прежде чем погрузиться в 12 различных техник, которые я рассмотрел. Каждый метод имеет собственную реализацию на Python, чтобы вы могли с ним хорошо познакомиться.

1. Что такое уменьшение размерности?

Мы ежедневно генерируем огромное количество данных. Фактически, 90% данных в мире было создано за последние 3-4 года! Цифры действительно ошеломляют. Ниже приведены лишь некоторые из примеров собираемых данных:

• Facebook собирает данные о том, что вам нравится, чем вы делитесь, что публикуете, о местах, которые вы посещаете, ресторанах, которые вам нравятся, и т. д.
• Приложения на вашем смартфоне собирают много личной информации о вас
• Amazon собирает данные о том, что вы покупаете, просматриваете, нажимаете и т. д. на их сайте.
• Казино отслеживают каждое движение каждого клиента.

По мере того, как генерация и сбор данных продолжает развиваться, визуализировать их и делать выводы становится все сложнее. Один из наиболее распространенных способов визуализации - это диаграммы. Предположим, у нас есть 2 переменные: возраст и рост. Мы можем использовать точечный или линейный график между возрастом и ростом и легко визуализировать их взаимосвязь:

Теперь рассмотрим случай, когда у нас есть, скажем, 100 переменных (p = 100). В этом случае у нас может быть 100 (100-1) / 2 = 5000 разных графиков. Визуализировать каждую из них по отдельности не имеет большого смысла, правда? В таких случаях, когда у нас есть большое количество переменных, лучше выбрать подмножество этих переменных (p << 100), которое захватывает столько же информации, сколько исходный набор переменных.

Давайте разберемся в этом на простом примере. Рассмотрим изображение ниже:

Здесь у нас есть веса подобных объектов в кг (X1) и фунтах (X2). Если мы используем обе эти переменные, они будут передавать аналогичную информацию. Таким образом, имеет смысл использовать только одну переменную. Мы можем преобразовать данные из 2D (X1 и X2) в 1D (Y1), как показано ниже:

Точно так же мы можем уменьшить p измерений данных до подмножества k измерений (k << n). Это называется уменьшением размерности.

2. Зачем требуется уменьшение размерности?

Вот некоторые из преимуществ применения уменьшения размерности к набору данных:

• Место, необходимое для хранения данных, уменьшается по мере уменьшения количества измерений.
• Меньшие размеры приводят к меньшему времени вычислений/обучения.
• Некоторые алгоритмы работают не очень хорошо, когда у нас большие размерности данных. Таким образом, уменьшение этих размерностей необходимо, чтобы алгоритм был полезен.
• Уменьшение размерности заботится о мультиколлинеарности, удаляя лишние признаки. Например, у вас есть две переменные - «время, проведенное на беговой дорожке в минутах» и «сожженные калории». Эти переменные сильно взаимосвязаны: чем больше времени вы проводите на беговой дорожке, тем больше калорий вы сжигаете. Следовательно, нет смысла хранить обе, поскольку только одна из них делает то, что вам нужно.
• Это помогает визуализировать данные. Как обсуждалось ранее, очень сложно визуализировать данные в более высоких измерениях, поэтому сокращение нашего пространства до 2D или 3D может позволить нам более четко строить и наблюдать закономерности.

Пришло время погрузиться в суть этой статьи - различные методы уменьшения размерности! Мы будем использовать набор данных из AV’s Practice Problem: Big Mart Sales III (зарегистрируйтесь по этой ссылке и загрузите набор данных из раздела data).

3. Распространенные методы уменьшения размерности

Уменьшение размерности можно осуществить двумя способами:

- сохраняя только самые релевантные переменные из исходного набора данных (этот метод называется выбором признаков);

- путем нахождения меньшего набора новых переменных, каждая из которых представляет собой комбинацию входных переменных, содержащих в основном ту же информацию, что и входные переменные (этот метод называется уменьшением размерности).

Теперь мы рассмотрим различные методы уменьшения размерности и то, как реализовать каждый из них в Python.

3.1 Доля отсутствующих значений.

Предположим, вам дан набор данных. Что было бы первым шагом в его использовании? Вы, естественно, захотите сначала изучить данные, прежде чем строить модель. Изучая данные, вы обнаруживаете, что в вашем наборе данных отсутствуют некоторые значения. Что теперь? Вы попытаетесь выяснить причину этих пропущенных значений, а затем заполнить их или полностью исключить переменные, для которых отсутствуют значения (используя соответствующие методы).

Что, если у нас слишком много пропущенных значений (скажем, более 50%)? Должны ли мы заполнять недостающие значения или исключить переменную? Я бы предпочел исключить переменную, так как в ней будет мало информации. Однако это не высечено в камне. Мы можем установить пороговое значение, и если процент пропущенных значений в любой переменной превышает этот порог, мы отбросим переменную.

Давайте реализуем этот подход в Python.

# import required libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

Сначала загрузим данные:

# read the data
train=pd.read_csv("Train_UWu5bXk.csv")

Примечание. При чтении данных должен быть добавлен путь к файлу.

Теперь мы проверим процент пропущенных значений в каждой переменной. Мы можем использовать .isnull().Sum(), чтобы вычислить его.

# checking the percentage of missing values in each variable
train.isnull().sum()/len(train)*100

Как видно из приведенной выше таблицы, пропущенных значений не так много (на самом деле они есть только у двух переменных). Мы можем заполнить эти значения, используя соответствующие методы, или мы можем установить порог, скажем, 20%, и удалить переменную, имеющую более 20% пропущенных значений. Давайте посмотрим, как это можно сделать в Python:

# saving missing values in a variable
a = train.isnull().sum()/len(train)*100
# saving column names in a variable
variables = train.columns
variable = [ ]
for i in range(0,12):
    if a[i]<=20:   #setting the threshold as 20%
        variable.append(variables[i])

Таким образом, используемые переменные хранятся в «variable», которая содержит только те признаки, в которых пропущенных значений меньше 20%.

3.2 Фильтр низкой дисперсии

Рассмотрим переменную в нашем наборе данных, где все наблюдения имеют одинаковое значение, скажем 1. Если мы будем использовать эту переменную, как вы думаете, она может улучшить модель, которую мы построим? Ответ - нет, потому что эта переменная будет иметь нулевую дисперсию.

Итак, нам нужно рассчитать дисперсию каждой переменной. Затем отбросьте переменные, имеющие низкую дисперсию по сравнению с другими переменными в нашем наборе данных. Причина этого, как я упоминал выше, заключается в том, что переменные с низкой дисперсией не влияют на целевую переменную.

Давайте сначала вычислим недостающие значения в столбце Item_Weight, используя среднее значение известных наблюдений Item_Weight. Для столбца Outlet_Size мы будем использовать моду известных значений Outlet_Size для заполнения отсутствующих значений:

train['Item_Weight'].fillna(train['Item_Weight'].median(), inplace=True)
train['Outlet_Size'].fillna(train['Outlet_Size'].mode()[0], inplace=True)

Проверим, все ли пропущенные значения заполнены:

train.isnull().sum()/len(train)*100

Вуаля! Мы все настроили. Теперь давайте посчитаем дисперсию всех числовых переменных.

train.var()

Как видно из приведенных выше выходных данных, дисперсия Item_Visibility намного меньше по сравнению с другими переменными. Мы можем спокойно пропустить этот столбец. Вот как мы применяем фильтр с низкой дисперсией. Давайте реализуем это на Python:

numeric = train[['Item_Weight', 'Item_Visibility', 'Item_MRP', 'Outlet_Establishment_Year']]
var = numeric.var()
numeric = numeric.columns
variable = [ ]
for i in range(0,len(var)):
    if var[i]>=10:   #setting the threshold as 10%
       variable.append(numeric[i+1])

Приведенный выше код дает нам список переменных с дисперсией больше 10.

3.3 Фильтр высокой корреляции

Высокая корреляция между двумя переменными означает, что они имеют схожие тенденции и, вероятно, несут схожую информацию. Это может резко снизить эффективность некоторых моделей (например, моделей линейной и логистической регрессии). Мы можем вычислить корреляцию между независимыми числовыми переменными. Если коэффициент корреляции превышает определенное пороговое значение, мы можем отбросить одну из переменных (выбор удаляемой переменной очень субъективен и всегда должен производиться с учетом предметной области).

В качестве общего правила мы должны оставить те переменные, которые показывают приличную или высокую корреляцию с целевой переменной.

Давайте выполним вычисление корреляции на Python. Сначала мы удалим зависимую переменную (Item_Outlet_Sales), а оставшиеся переменные сохраним в новом фрейме данных (df).

df=train.drop('Item_Outlet_Sales', 1)
df.corr()

Замечательно, в нашем наборе данных нет переменных с высокой корреляцией. Как правило, если корреляция между парой переменных превышает 0,5–0,6, нам следует серьезно подумать об исключении одной из этих переменных.

3.4 Random Forest

Random Forest - один из наиболее широко используемых алгоритмов выбора признаков. Он поставляется со встроенной функцией важности, поэтому вам не нужно программировать ее отдельно. Он поможет нам выбрать меньший набор признаков.

Нам нужно преобразовать данные в числовую форму, применив одну хитрость, поскольку Random Forest (реализация Scikit-Learn) принимает только числовые входные данные. Давайте также отбросим переменные идентификаторы (Item_Identifier и Outlet_Identifier), поскольку это просто уникальные числа и в настоящее время не имеют для нас особого значения.

from sklearn.ensemble import RandomForestRegressor
df=df.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1)
model = RandomForestRegressor(random_state=1, max_depth=10)
df=pd.get_dummies(df)
model.fit(df,train.Item_Outlet_Sales)

После подбора модели постройте график важности признаков:

features = df.columns
importances = model.feature_importances_
indices = np.argsort(importances)[-9:]  # top 10 features
plt.title('Feature Importances')
plt.barh(range(len(indices)), importances[indices], color='b', align='center')
plt.yticks(range(len(indices)), [features[i] for i in indices])
plt.xlabel('Relative Importance')
plt.show()

Основываясь на приведенном выше графике, мы можем вручную выбрать самые важные признаки, чтобы уменьшить размерность в нашем наборе данных. Чтобы сделать это, мы можем использовать функцию SelectFromModel из sklearn. Она выбирает признаки в зависимости от важности их веса.

from sklearn.feature_selection import SelectFromModel
feature = SelectFromModel(model)
Fit = feature.fit_transform(df, train.Item_Outlet_Sales)

3.5 Метод обратного исключения

Выполните следующие шаги, чтобы понять и использовать технику «метод обратного исключения»:

• Сначала мы берем все n переменных, присутствующих в нашем наборе данных, и обучаем модель, используя их.
• Затем мы рассчитываем эффективность модели.
• Теперь мы вычисляем эффективность модели после исключения каждой переменной (n раз), т.е. мы отбрасываем по одной переменной каждый раз и обучаем модель на оставшихся n-1 переменных.
• Мы определяем переменную, удаление которой привело к наименьшему (или отсутствию) изменения эффективности модели, а затем отбрасываем эту переменную.
• Повторяйте этот процесс до тех пор, пока никакие переменные не будут удаляться.
• Этот метод можно использовать при построении моделей линейной регрессии или логистической регрессии. Давайте посмотрим на реализацию Python:

from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import RFE
from sklearn import datasets
lreg = LinearRegression()
rfe = RFE(lreg, 10)
rfe = rfe.fit_transform(df, train.Item_Outlet_Sales)

Нам нужно указать алгоритм и количество признаков для выбора, и мы вернем список переменных, полученный в результате обратного исключения признаков. Мы также можем проверить ранжирование переменных с помощью команды «rfe.ranking_».

'''

DIMENSIONALITY REDUCTION - BACKWARD FEATURE ELIMINATION

'''

# importing required libraries

import pandas as pd

from sklearn.linear_model import LinearRegression

from sklearn.feature_selection import RFE

# read the data

train = pd.read_csv('train.csv')

print(train.head())

# seperate the target and independent variable

X = train.drop(columns = ['Item_Outlet_Sales'],axis=1)

Y = train['Item_Outlet_Sales']

# create the object of the model

lreg = LinearRegression()

# specify the number of features to select

rfe = RFE(lreg, 10)

# fit the model

rfe = rfe.fit(X, Y)

print('\n\nFEATUERS SELECTED\n\n')

print(rfe.support_)

print('\n\nRANKING OF FEATURES\n\n')

print(rfe.ranking_)

3.6 Метод прямого выбора

Это процесс, противоположный процессу обратного исключения, который мы видели выше. Вместо того, чтобы исключать признаки, мы пытаемся найти лучшие признаки, которые улучшают характеристики модели. Этот метод работает следующим образом:

• Начнем с одного признака. По сути, мы обучаем модель n раз, используя каждый признак отдельно.
• Переменная, дающая наилучшую эффективность, выбирается в качестве начальной.
• Затем мы повторяем этот процесс и добавляем по одной переменной за раз. Переменная, обеспечивающая наибольшее повышение эффективности, сохраняется.
• Мы повторяем этот процесс до тех пор, пока не увидим значительных улучшений в эффективности модели.

Давайте реализуем это на Python:

from sklearn.feature_selection import f_regression
ffs = f_regression(df,train.Item_Outlet_Sales )

Этот код возвращает массив, содержащий F-значения переменных и p-значения, соответствующие каждому F-значению. Перейдите по этой ссылке, чтобы узнать больше о F-значениях. Для нашей цели мы выберем переменные, имеющие F больше 10:

variable = [ ]
for i in range(0,len(df.columns)-1):
    if ffs[0][i] >=10:
       variable.append(df.columns[i])

Это дает нам наибольшее количество переменных на основе алгоритма прямого исключения.

ПРИМЕЧАНИЕ. Оба эти алгоритма требуют много времени и вычислительно дороги. Они практически используются только для наборов данных с небольшим количеством входных переменных.

Методы, которые мы видели до сих пор, обычно используются, когда у нас не очень большое количество переменных в нашем наборе данных. Это более или менее приемы выбора признаков. В следующих разделах мы будем работать с набором данных Fashion MNIST, который состоит из изображений, принадлежащих к разным типам одежды, например футболка, брюки, сумка и т. д. Набор данных можно загрузить из практической задачи «IDENTIFY THE APPAREL».

В наборе данных в общей сложности 70 000 изображений, из которых 60 000 находятся в обучающем наборе, а остальные 10 000 - это тестовые изображения. В рамках данной статьи мы будем работать только с обучающими изображениями. Файл в формате zip. Как только вы распакуете zip-файл, вы получите файл .csv и папку train, в которой находятся эти 60 000 изображений. Соответствующий ярлык каждого изображения можно найти в файле «train.csv».

3.7 Факторный анализ

Предположим, у нас есть две переменные: доход и образование. Эти переменные потенциально будут иметь высокую корреляцию, поскольку люди с более высоким уровнем образования, как правило, имеют значительно более высокий доход, и наоборот.

В методике факторного анализа переменные группируются по их корреляциям, то есть все переменные в определенной группе будут иметь высокую корреляцию между собой, но низкую корреляцию с переменными другой группы (групп). Здесь каждая группа известна как фактор. Этих факторов мало по сравнению с исходными размерами данных. Однако эти факторы трудно заметить.

Давайте сначала прочитаем все изображения, содержащиеся в папке train:

import pandas as pd
import numpy as np
from glob import glob
import cv2
images = [cv2.imread(file) for file in glob('train/*.png')]

ПРИМЕЧАНИЕ. Вы должны заменить путь внутри функции glob на путь к папке train.

Теперь мы преобразуем эти изображения в формат массива numpy, чтобы мы могли выполнять математические операции, а также строить графики.

images = np.array(images)
images.shape

(60000, 28, 28, 3)

Как видно выше, это трехмерный массив. Мы должны преобразовать его в одномерный, так как все будущие методы принимают только одномерный ввод. Для этого нам нужно сгладить изображения:

image = []
for i in range(0,60000):
    img = images[i].flatten()
    image.append(img)
image = np.array(image)

Давайте теперь создадим dataframe, содержащий значения пикселей каждого отдельного пикселя, присутствующего в каждом изображении, а также их соответствующие метки (для меток мы будем использовать файл train.csv).

train = pd.read_csv("train.csv")     # Give the complete path of your train.csv file
feat_cols = [ 'pixel'+str(i) for i in range(image.shape[1]) ]
df = pd.DataFrame(image,columns=feat_cols)
df['label'] = train['label']

Теперь разберем набор данных с помощью факторного анализа:

from sklearn.decomposition import FactorAnalysis
FA = FactorAnalysis(n_components = 3).fit_transform(df[feat_cols].values)

Здесь n_components будет определять количество факторов в преобразованных данных. После преобразования данных пора визуализировать результаты:

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(12,8))
plt.title('Factor Analysis Components')
plt.scatter(FA[:,0], FA[:,1])
plt.scatter(FA[:,1], FA[:,2])
plt.scatter(FA[:,2],FA[:,0])

Выглядит потрясающе, не правда ли? Мы можем видеть все различные факторы на приведенном выше графике. Здесь по оси x и оси y представлены значения разложенных факторов. Как я уже упоминал ранее, эти факторы трудно наблюдать по отдельности, но мы смогли успешно уменьшить размеры наших данных.

3.8 Анализ главных компонентов (PCA)

PCA - это метод, который помогает нам извлечь новый набор переменных из существующего большого набора переменных. Эти извлеченные переменные называются главными компонентами. Вы можете обратиться к этой статье, чтобы узнать больше о PCA. Для краткого ознакомления ниже приведены некоторые из ключевых моментов, которые вам следует знать о PCA, прежде чем продолжить:

• главный компонент - это линейная комбинация исходных переменных;
• основные компоненты извлекаются таким образом, что первый главный компонент объясняет максимальную дисперсию в наборе данных;
• второй главный компонент пытается объяснить оставшуюся дисперсию в наборе данных и не коррелирует с первым главным компонентом;
• третий главный компонент пытается объяснить дисперсию, которая не объясняется первыми двумя главными компонентами и т. д.

Прежде чем двигаться дальше, мы случайным образом построим некоторые изображения из нашего набора данных:

rndperm = np.random.permutation(df.shape[0])
plt.gray()
fig = plt.figure(figsize=(20,10))
for i in range(0,15):
    ax = fig.add_subplot(3,5,i+1)
    ax.matshow(df.loc[rndperm[i],feat_cols].values.reshape((28,28*3)).astype(float))

Давайте реализуем PCA с помощью Python и преобразуем набор данных:

from sklearn.decomposition import PCA
pca = PCA(n_components=4)
pca_result = pca.fit_transform(df[feat_cols].values)

В этом случае n_components будет определять количество главных компонентов в преобразованных данных. Давайте представим себе, насколько дисперсия объясняется с помощью этих 4 компонентов. Мы будем использовать explained_variance_ratio_, чтобы вычислить то же самое.

plt.plot(range(4), pca.explained_variance_ratio_)
plt.plot(range(4), np.cumsum(pca.explained_variance_ratio_))
plt.title("Component-wise and Cumulative Explained Variance")

На приведенном выше графике синяя линия представляет покомпонентную объясненную дисперсию, а оранжевая линия представляет совокупную объясненную дисперсию. Мы можем объяснить около 60% дисперсии в наборе данных, используя всего четыре компонента. Давайте теперь попробуем визуализировать каждый из этих разложенных компонентов:

import seaborn as sns
plt.style.use('fivethirtyeight')
fig, axarr = plt.subplots(2, 2, figsize=(12, 8))
sns.heatmap(pca.components_[0, :].reshape(28, 84), ax=axarr[0][0], cmap='gray_r')
sns.heatmap(pca.components_[1, :].reshape(28, 84), ax=axarr[0][1], cmap='gray_r')
sns.heatmap(pca.components_[2, :].reshape(28, 84), ax=axarr[1][0], cmap='gray_r')
sns.heatmap(pca.components_[3, :].reshape(28, 84), ax=axarr[1][1], cmap='gray_r')
axarr[0][0].set_title(
"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[0]*100),
fontsize=12
)
axarr[0][1].set_title(
"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[1]*100),
fontsize=12
)
axarr[1][0].set_title(
"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[2]*100),
fontsize=12
)
axarr[1][1].set_title(
"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[3]*100),
fontsize=12
)
axarr[0][0].set_aspect('equal')
axarr[0][1].set_aspect('equal')
axarr[1][0].set_aspect('equal')
axarr[1][1].set_aspect('equal')

plt.suptitle('4-Component PCA')

Каждое дополнительное измерение, которое мы добавляем к методу PCA, улавливает все меньшую и меньшую дисперсию модели. Первый компонент является наиболее важным, за ним следует второй, затем третий и так далее.

Мы также можем использовать Singular Value Decomposition (SVD), чтобы разложить наш исходный набор данных на его составляющие, что приведет к снижению размерности. Чтобы узнать о математике, лежащей в основе SVD, обратитесь к этой статье.

SVD раскладывает исходные переменные на три составляющие матрицы. По сути, он используется для удаления избыточных признаков из набора данных. Он использует концепцию собственных значений и собственных векторов для определения этих трех матриц. Мы не будем вдаваться в математику этого вопроса из-за объема этой статьи, но давайте придерживаться нашего плана, то есть уменьшения размеров в нашем наборе данных.

Давайте реализуем SVD и разложим наши исходные переменные:

from sklearn.decomposition import TruncatedSVD 
svd = TruncatedSVD(n_components=3, random_state=42).fit_transform(df[feat_cols].values)

Давайте визуализируем преобразованные переменные, построив первые два главных компонента:

plt.figure(figsize=(12,8))
plt.title('SVD Components')
plt.scatter(svd[:,0], svd[:,1])
plt.scatter(svd[:,1], svd[:,2])
plt.scatter(svd[:,2],svd[:,0])

Приведенный выше график рассеяния очень четко показывает нам разложенные компоненты. Как описано ранее, между этими компонентами нет большой корреляции.

3.9 Анализ независимых компонент

Анализ независимых компонент (ICA) основан на теории информации и также является одним из наиболее широко используемых методов уменьшения размерности. Основное различие между PCA и ICA заключается в том, что PCA ищет некоррелированные факторы, а ICA ищет независимые факторы.

Если две переменные не коррелированы, это означает, что между ними нет линейной связи. Если они независимы, это означает, что они не зависят от других переменных. Например, возраст человека не зависит от того, что он ест или сколько он смотрит телевизор.

Этот алгоритм предполагает, что данные переменные являются линейной комбинацией некоторых неизвестных скрытых переменных. Также предполагается, что эти скрытые переменные взаимно независимы, то есть они не зависят от других переменных, и поэтому они называются независимыми компонентами наблюдаемых данных.

Давайте сравним PCA и ICA визуально, чтобы лучше понять, чем они отличаются:

Здесь рисунок (a) представляет результаты PCA, а рисунок (b) представляет результаты ICA для того же набора данных.

Уравнение PCA - это: x = Wχ.

Здесь,

x - наблюдения;

W - матрица смешения;

χ - источник или независимые компоненты.

Теперь нам нужно найти матрицу несмешивания, чтобы компоненты стали как можно более независимыми. Наиболее распространенный метод измерения независимости компонентов - это негауссовость:

Согласно центральной предельной теореме, распределение суммы независимых компонентов имеет тенденцию к нормальному распределению (гауссову).

Таким образом, мы можем искать преобразования, которые максимизируют эксцесс каждого компонента независимых компонентов. Эксцесс - это момент распределения третьего порядка. Чтобы узнать больше о эксцессе, перейдите сюда.

Максимальное увеличение эксцесса сделает распределение негауссовым, и, следовательно, мы получим независимые компоненты.

Вышеуказанное распределение не является гауссовым, что, в свою очередь, делает компоненты независимыми. Попробуем реализовать ICA на Python:

from sklearn.decomposition import FastICA 
ICA = FastICA(n_components=3, random_state=12) 
X=ICA.fit_transform(df[feat_cols].values)

Здесь n_components будет определять количество компонентов в преобразованных данных. Мы преобразовали данные в 3 компонента с помощью ICA. Давайте посмотрим, насколько хорошо он преобразовал данные:

plt.figure(figsize=(12,8))
plt.title('ICA Components')
plt.scatter(X[:,0], X[:,1])
plt.scatter(X[:,1], X[:,2])
plt.scatter(X[:,2], X[:,0])

Данные были разделены на различные независимые компоненты, которые очень четко видны на рисунке выше. Ось X и ось Y представляют собой значение разложенных независимых компонентов.

Теперь мы рассмотрим некоторые методы, которые уменьшают размер данных с помощью методов проекции.

3.10 Методы, основанные на проекциях

Для начала нам нужно понять, что такое проекция. Предположим, у нас есть два вектора, вектор a и вектор b, как показано ниже:

Мы хотим найти проекцию a на b. Пусть угол между a и b равен. Проекция (a1) будет выглядеть так:

a1 - вектор, параллельный b. Итак, мы можем получить проекцию вектора a на вектор b, используя следующее уравнение:

Здесь,

a1 = проекция a на b;

b̂ = единичный вектор в направлении b.

Проецируя один вектор на другой, можно уменьшить размерность.

В методах проецирования многомерные данные представляются путем проецирования их точек на пространство меньшей размерности. Теперь поговорим о различных методах проекций:

Проекция на интересные направления:

Интересные направления зависят от конкретных проблем, но в целом направления, прогнозируемые значения которых не являются гауссовскими, считаются интересными.

Подобно ICA (Independent Component Analysis), проекция ищет направления, максимизирующие эксцесс прогнозируемых значений как меру негауссовости.

Проекция на многообразия:

Когда-то считалось, что Земля плоская. Куда бы вы ни пошли на Земле, она всегда выглядит плоской (давайте на время не будем обращать внимание на горы). Но если вы продолжите идти в одном направлении, вы окажетесь там, где начали. Этого бы не произошло, если бы Земля была плоской. Земля выглядит плоской только потому, что мы крошечные по сравнению с размером Земли.

Эти небольшие участки, на которых Земля выглядит плоской, представляют собой многообразия, и если мы объединим все эти многообразия, мы получим крупномасштабный вид Земли, то есть исходные данные. Точно так же для n-мерной кривой маленькие плоские части являются многообразиями, и комбинация этих многообразий даст нам исходную n-мерную кривую. Давайте посмотрим на шаги для проектирования на многообразия:

• Сначала ищем многообразие, близкое к данным.
• Затем спроецируйте данные на это многообразие.
• Наконец, для представления развернем многообразие.

Существуют различные методы получения многообразия, и все они состоят из трех этапов:

• Сбор информации из каждой точки данных для построения графика с точками данных в качестве вершин.
• Преобразование сгенерированного выше графика в подходящий вход для встраивания шагов.
• Вычисление собственного уравнения (nXn).

Давайте разберемся с техникой проекции на многообразие на примере.

Если многообразие непрерывно дифференцируемо до любого порядка, оно известно как гладкое или дифференцируемое многообразие. ISOMAP - это алгоритм, целью которого является восстановление полного низкоразмерного представления нелинейного многообразия. Предполагается, что многообразие гладкое.

Также предполагается, что для любой пары точек на многообразии геодезическое расстояние (кратчайшее расстояние между двумя точками на искривленной поверхности) между двумя точками равно евклидову расстоянию (кратчайшее расстояние между двумя точками на прямой). Давайте сначала визуализируем геодезическое и евклидово расстояние между парой точек:

Здесь,

Dn1n2 = геодезическое расстояние между X1 и X2.

dn1n2 = евклидово расстояние между X1 и X2.

ISOMAP предполагает, что оба эти расстояния равны. Давайте теперь посмотрим на более подробное объяснение этой техники. Как упоминалось ранее, все эти методы работают по трехступенчатому подходу. Мы подробно рассмотрим каждый из этих шагов:

График окрестностей:

Первый шаг - вычислить расстояние между всеми парами точек данных:

dij = dχ(xi,xj) = || xi-xj || χ

Здесь,

dχ(xi, xj) = геодезическое расстояние между xi и xj

|| xi-xj || = евклидово расстояние между xi и xj

После расчета расстояния мы определяем, какие точки данных являются соседями в многообразии.

Наконец, создается граф соседства: G = G (V, ℰ), где набор вершин V = {x1, x2,…., Xn} - это точки входных данных, а набор ребер ℰ = {eij} указывает на взаимосвязь соседства между точками.

Расчет расстояний на графе:

Теперь вычислим геодезическое расстояние между парами точек многообразия по расстояниям на графе.

Расстояние на графе - это расстояние по кратчайшему пути между всеми парами точек на графе G.

Встраивание:

• Когда у нас есть расстояния, мы формируем симметричную (nXn) матрицу квадратов расстояний в графе.
• Теперь мы выбираем вложенные векторы, чтобы минимизировать разницу между геодезическим расстоянием и расстоянием на графике.
• Наконец, граф G вкладывается в Y.

Давайте реализуем это на Python и получим более четкое представление, о чем я говорю. Мы выполним нелинейное уменьшение размерности с помощью Isometric Mapping. Для визуализации мы возьмем только подмножество нашего набора данных, так как его запуск для всего набора данных потребует много времени.

from sklearn import manifold 
trans_data = manifold.Isomap(n_neighbors=5, n_components=3, n_jobs=-1).fit_transform(df[feat_cols][:6000].values)

Используемые параметры:

n_neighbors определяет количество соседей для каждой точки.

n_components определяет количество координат для многообразия.

n_jobs = -1 будет использовать все доступные ядра ЦП

Визуализация преобразованных данных:

plt.figure(figsize=(12,8))
plt.title('Decomposition using ISOMAP')
plt.scatter(trans_data[:,0], trans_data[:,1])
plt.scatter(trans_data[:,1], trans_data[:,2])
plt.scatter(trans_data[:,2], trans_data[:,0])

Выше видно, что корреляция между этими компонентами очень мала. Фактически, они даже менее коррелированы по сравнению с компонентами, которые мы получили с помощью SVD ранее!

3.11 Стохастическое вложение соседей с t-распределением (t-SNE)

До сих пор мы знали, что PCA - хороший выбор для уменьшения размерности и визуализации наборов данных с большим количеством переменных. Но что, если бы мы могли использовать что-то более продвинутое? Что, если мы сможем легко искать закономерности нелинейным способом? t-SNE - один из таких методов. В целом есть два типа подходов, которые мы можем использовать для сопоставления точек данных:

• Локальные подходы: они сопоставляют близлежащие точки на многообразии с близлежащими точками в низкоразмерном представлении.
• Глобальные подходы: они пытаются сохранить геометрию во всех масштабах, т. е. сопоставляют близлежащие точки на многообразии с соседними точками в низкоразмерном представлении, а также удаленные точки с удаленными точками.

t-SNE - один из немногих алгоритмов, способных одновременно сохранять как локальную, так и глобальную структуру данных. 

Он вычисляет вероятность подобия точек в пространстве большой размерности, а также в пространстве низкой размерности. 

Многомерные евклидовы расстояния между точками данных преобразуются в условные вероятности, которые представляют собой сходства:

xi и xj - точки данных, || xi-xj || представляет евклидово расстояние между этими точками данных, а 𝛔i - дисперсия точек данных в многомерном пространстве.

Для низкоразмерных точек данных yi и yj, соответствующих многомерным точкам данных xi и xj, можно вычислить аналогичную условную вероятность, используя:

где || yi-yj || представляет собой евклидово расстояние между yi и yj.

После вычисления обеих вероятностей он минимизирует разницу между обеими вероятностями.

Вы можете обратиться к этой статье, чтобы узнать о t-SNE более подробно.

Теперь мы реализуем его на Python и визуализируем результаты:

from sklearn.manifold import TSNE 
tsne = TSNE(n_components=3, n_iter=300).fit_transform(df[feat_cols][:6000].values)

n_components будет определять количество компонентов в преобразованных данных. Пришло время визуализировать преобразованные данные:

plt.figure(figsize=(12,8))
plt.title('t-SNE components')
plt.scatter(tsne[:,0], tsne[:,1])
plt.scatter(tsne[:,1], tsne[:,2])
plt.scatter(tsne[:,2], tsne[:,0])

Здесь вы можете ясно увидеть различные компоненты, которые были преобразованы с помощью мощной техники t-SNE.

3.12 UMAP

t-SNE очень хорошо работает с большими наборами данных, но у него также есть ограничения, такие как потеря крупномасштабной информации, большое время вычислений и неспособность осмысленно представлять очень большие наборы данных. Uniform Manifold Approximation and Projection (UMAP) - это метод уменьшения размерности, который может сохранить как большую часть локальной, так и более глобальной структуры данных по сравнению с t-SNE, с более коротким временем выполнения. Звучит интригующе, правда?

Некоторые из ключевых преимуществ UMAP:

• Он может обрабатывать большие наборы данных и данные большого размера без особых трудностей.
• Он сочетает в себе мощность визуализации с возможностью уменьшения размеров данных.
• Наряду с сохранением локальной структуры он также сохраняет глобальную структуру данных. UMAP сопоставляет близлежащие точки на многообразии с близлежащими точками в низкоразмерном представлении и делает то же самое для удаленных точек.

Этот метод использует концепцию k-ближайших соседей и оптимизирует результаты с помощью стохастического градиентного спуска. Сначала он вычисляет расстояние между точками в пространстве большой размерности, проецирует их на пространство низкой размерности и вычисляет расстояние между точками в этом пространстве низкой размерности. Затем он использует стохастический градиентный спуск, чтобы минимизировать разницу между этими расстояниями. Чтобы получить более полное представление о том, как работает UMAP, ознакомьтесь с этой статьей.

Обратитесь сюда, чтобы увидеть документацию и руководство по установке UMAP. Теперь реализуем его на Python:

import umap
umap_data = umap.UMAP(n_neighbors=5, min_dist=0.3, n_components=3).fit_transform(df[feat_cols][:6000].values)

Здесь,

n_neighbors определяет количество используемых соседних точек.

min_dist управляет допустимой плотностью встраивания. Большие значения обеспечивают более равномерное распределение встроенных точек.

Визуализируем трансформацию:

plt.figure(figsize=(12,8))
plt.title('Decomposition using UMAP')
plt.scatter(umap_data[:,0], umap_data[:,1])
plt.scatter(umap_data[:,1], umap_data[:,2])
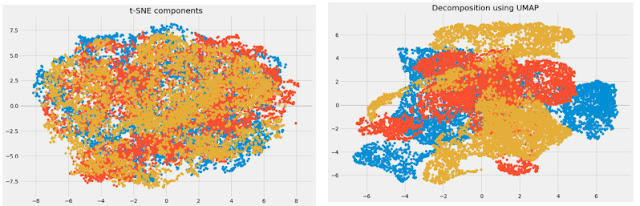
plt.scatter(umap_data[:,2], umap_data[:,0])

Размерность была уменьшена, и мы можем визуализировать различные преобразованные компоненты. Между преобразованными переменными очень слабая корреляция. Сравним результаты UMAP и t-SNE:

Мы видим, что корреляция между компонентами, полученными из UMAP, намного меньше по сравнению с корреляцией между компонентами, полученными из t-SNE. Следовательно, UMAP дает лучшие результаты.

Как упоминалось в репозитории GitHub UMAP, он часто лучше справляется с сохранением аспектов глобальной структуры данных, чем t-SNE. Это означает, что он часто может обеспечить лучшую «общую картину» данных, а также сохранить отношения между соседями.

Сделайте глубокий вдох. Мы рассмотрели довольно много методов уменьшения размерности. Кратко подытожим, где можно использовать каждый из них.

4. Краткое изложение того, когда использовать каждый метод уменьшения размерности.

В этом разделе мы кратко резюмируем варианты использования каждого метода уменьшения размерности, который мы рассмотрели. Важно понимать, где можно и нужно использовать определенную технику, поскольку это помогает сэкономить время, усилия и вычислительную мощность.

Доля отсутствующих значений: если в наборе данных слишком много пропущенных значений, мы используем этот подход, чтобы уменьшить количество переменных. Мы можем отбросить переменные с большим количеством пропущенных значений в них.

Фильтр низкой дисперсии: мы применяем этот подход для выявления и удаления постоянных переменных из набора данных. На целевую переменную не влияют переменные с низкой дисперсией, поэтому эти переменные можно безопасно отбросить.

Фильтр высокой корреляции: пара переменных, имеющих высокую корреляцию, увеличивает мультиколлинеарность в наборе данных. Таким образом, мы можем использовать этот метод, чтобы найти сильно коррелированные признаки и удалить их.

Random Forest: это один из наиболее часто используемых методов, который говорит нам о важности каждой функции, присутствующей в наборе данных. Мы можем определить важность каждой функции и сохранить большинство функций, что приведет к снижению размерности.

Как методы обратного исключения признаков, так и методы прямого выбора, отнимают много вычислительного времени и, следовательно, обычно используются для небольших наборов данных.

Факторный анализ: этот метод лучше всего подходит для ситуаций, когда у нас есть сильно коррелированный набор переменных. Он делит переменные на основе их корреляции на разные группы и сопоставляет каждую группу с фактором.

Анализ главных компонент: это один из наиболее широко используемых методов работы с линейными данными. Он разделяет данные на набор компонентов, которые пытаются объяснить как можно большую дисперсию.

Анализ независимых компонент: мы можем использовать ICA для преобразования данных в независимые компоненты, которые описывают данные с использованием меньшего количества компонентов.

ISOMAP: мы используем эту технику, когда данные сильно нелинейны.

t-SNE: этот метод также хорошо работает, когда данные сильно нелинейны. Он отлично работает и для визуализаций.

UMAP: этот метод хорошо работает для данных большого размера. Его время работы меньше по сравнению с t-SNE.

Заключение

Это самая исчерпывающая статья о снижении размерности, которую вы сможете найти! Мне было очень весело писать его, и я нашел несколько новых способов работы с большим количеством переменных, которые я раньше не использовал (например, UMAP).

Работа с тысячами и миллионами признаков - обязательный навык для любого специалиста по данным. Объем данных, которые мы генерируем каждый день, беспрецедентен, и нам нужно найти разные способы выяснить, как их использовать. Снижение размерности - очень полезный способ сделать это, и он творит чудеса для меня как в профессиональной среде, так и на хакатонах машинного обучения.