Введение
Интерпретация того, как работает модель, - один из самых важных аспектов науки о данных. Вы строите модель, которая дает довольно впечатляющие результаты, но какой процесс стоял за этим? Как специалисту по анализу данных, вам необходимо получить ответ на этот часто задаваемый вопрос.
Например, предположим, что вы построили модель для прогнозирования курса акций компании. Вы заметили, что цена акций быстро выросла за ночь. Причин может быть несколько. Определение вероятности наиболее правдоподобной причины - вот в чем суть оценки максимального правдоподобия. Эта концепция используется, среди прочего, в экономике, МРТ, спутниковой съемке.
В этом посте мы рассмотрим, как работает оценка максимального правдоподобия (далее MLE) и как ее можно использовать для определения коэффициентов модели с любым типом распределения. Понимание MLE потребует знания теории вероятности и математики, но я постараюсь облегчить его на примерах.
Почему я должен использовать оценку максимального правдоподобия (MLE)?
Допустим, мы хотим спрогнозировать продажу билетов на мероприятие. Данные имеют следующую гистограмму и плотность.
Как бы вы смоделировали такую переменную? Переменная не имеет нормального распределения, асимметрична и, следовательно, нарушает предположения о линейной регрессии. Популярным способом является преобразование переменной с помощью log, sqrt, обратных величин и т.д., чтобы преобразованная переменная имела нормальное распределение и могла быть смоделирована с помощью линейной регрессии.
Давайте попробуем эти преобразования и посмотрим, каковы результаты:
Логарифмическое преобразование:
Преобразование квадратного корня:
Обратное преобразование:
Ни одно из них не близко к нормальному распределению. Как нам моделировать такие данные, чтобы не нарушались основные предположения модели? Как насчет моделирования этих данных с другим распределением, а не с нормальным? Если мы воспользуемся другим распределением, как мы будем оценивать коэффициенты?
Вот где такое большое преимущество имеет оценка максимального правдоподобия (MLE).
Понимание MLE на примере
Изучая статистику и теорию вероятности, вы, должно быть, сталкивались с подобными задачами: какова вероятность x> 100, учитывая, что x следует нормальному распределению со средним значением 50 и стандартным отклонением (sd) 10. В таких задачах мы уже знаем распределение (в данном случае нормальное) и его параметры (среднее и стандартное отклонение), но в реальных задачах эти величины неизвестны и должны оцениваться на основе данных. MLE - это метод, который помогает нам определить параметры распределения, которые лучше всего описывают данные.
Давайте разберемся с этим на примере. Предположим, у нас есть точки данных, представляющие вес (в килограммах) учащихся в классе. Точки данных показаны на рисунке ниже (также предоставляется код R, который использовался для создания графика):
x = as.data.frame(rnorm(50,50,10)) ggplot(x, aes(x = x)) + geom_dotplot()
Похоже, это соответствует нормальному распределению. Но как получить среднее значение и стандартное отклонение (sd) для этого распределения? Один из способов - напрямую вычислить среднее значение и стандартное отклонение заданных данных, которые составляют 49,8 кг и 11,37 соответственно. Эти значения являются хорошим представлением этих данных, но могут не лучшим образом всего описывать совокупность.
Мы можем использовать MLE, чтобы получить более надежные оценки параметров. Таким образом, MLE может быть определен как метод оценки параметров совокупности (таких как среднее значение и дисперсия для нормального, лямбда для пуассоновского и т. д.) на основе выборочных данных, так что вероятность (правдоподобие) получения наблюдаемых данных максимальна.
Чтобы получить интуитивное представление о MLE, попробуйте угадать, что из следующего может максимизировать вероятность наблюдения данных на приведенном выше рисунке?
Mean = 100, SD = 10
Mean = 50, SD = 10
Маловероятно, что мы увидим вышеуказанную форму данных, если среднее значение генеральной совокупности равно 100.
Знакомство с техническими деталями
Теперь, когда у вас есть интуитивное представление о том, что может делать MLE, мы можем подробно разобраться в том, что такое на самом деле вероятность и как ее можно максимизировать. Но сначала давайте начнем с быстрого обзора параметров распределения.
Параметры распределения
Давайте сначала разберемся с параметрами распределения. Википедия определяет этот термин следующим образом: «Это величина, которая индексирует семейство распределений вероятностей». Его можно рассматривать как числовую характеристику популяции или статистическую модель. Мы можем понять это по следующей диаграмме:
Рисунок 2, источник: Википедия.
Ширина и высота колоколообразной кривой определяется двумя параметрами - средним значением и дисперсией. Они известны как параметры распределения для нормального распределения. Точно так же распределение Пуассона регулируется одним параметром - лямбда, который представляет собой количество раз, когда событие происходит в интервале времени или пространства.
Рисунок 3, источник: Википедия.
Большинство распределений имеют один или два параметра, но некоторые распределения могут иметь до 4 параметров, например бета-распределение с 4 параметрами.
Правдоподобие
Из рис. 2 и 3 видно, что при заданном наборе параметров распределения некоторые значения данных более вероятны, чем другие данные. Из рис. 1 мы видели, что указанные данные более вероятны, когда среднее значение равно 50, а не 100. В действительности, однако, мы уже видели данные. Соответственно, мы сталкиваемся с обратной проблемой: учитывая наблюдаемые данные и интересующую модель, нам нужно найти одну функцию плотности вероятности/функцию вероятности (f (x| θ)) среди всех плотностей вероятностей, которые наиболее вероятно соответствуют этим данным.
Чтобы решить эту обратную задачу, мы определяем функцию правдоподобия, меняя роли вектора данных x и вектора параметров (распределения) θ в f (x | θ), т. е.
L(θ;x) = f(x| θ)
В MLE мы можем предположить, что у нас есть функция правдоподобия L (θ; x), где θ - вектор параметра распределения, а x - набор наблюдений. Мы заинтересованы в нахождении значения θ, которое максимизирует правдоподобность с наблюдаемыми данными (значениями x).
Логарифмическое правдоподобие
Рассматриваемая математическая проблема упрощается, если мы предположим, что наблюдения (xi) являются независимыми и одинаково распределенными случайными величинами, взятыми из распределения вероятностей, f0 (где f0 = нормальное распределение, например, на рисунке 1). Это сокращает функцию правдоподобия до:
Чтобы найти максимумы/минимумы этой функции, мы можем взять производную этой функции по t θ и приравнять ее к 0 (поскольку нулевой наклон указывает на максимумы или минимумы). Поскольку здесь есть произведение, нам нужно применить правило цепочки, которое довольно громоздко для произведений. Умный трюк - взять логарифм функции правдоподобия и максимизировать ее. Это преобразует произведение в сумму, и поскольку логарифм является строго возрастающей функцией, это не повлияет на результирующее значение θ. Итак, мы имеем:
Максимизация правдоподобия
Чтобы найти максимумы логарифмической функции правдоподобия LL(θ; x), мы можем сделать следующее:
- Возьмем первую производную функции LL (θ; x) по t θ и приравняем ее к 0.
- Возьмем вторую производную функции LL (θ; x) по t θ и убедимся, что она отрицательна.
Есть много ситуаций, когда математический анализ не может напрямую максимизировать правдоподобие, но максимум все же можно легко определить. Нет ничего, что дало бы первой производной, равной нулю, какое-либо «первенство» или особое место при нахождении значения (значений) параметра, которое максимизирует логарифмическое правдоподобие. Это просто удобный инструмент, когда нужно оценить несколько параметров.
В качестве общего принципа практически любой допустимый подход для определения argmax функции может быть подходящим для нахождения максимумов функции логарифмического правдоподобия. Это задача неограниченной нелинейной оптимизации. Мы ищем алгоритм оптимизации, который ведет себя следующим образом:
- Надежно сходится к локальному минимизатору с произвольной начальной точки.
- Делает это как можно быстрее.
Очень распространено использование методов оптимизации для максимизации правдоподобия; существует большое разнообразие методов (метод Ньютона, оценка Фишера, различные подходы на основе сопряженных градиентов, наискорейший спуск, подходы типа Нелдера-Мида (симплекс), BFGS и множество других методов).
Оказывается, когда предполагается, что модель является гауссовой, как в примерах выше, оценки MLE эквивалентны обычному методу наименьших квадратов.
Вы можете обратиться к доказательству здесь.
Определение коэффициентов модели с использованием MLE
Давайте теперь посмотрим, как MLE можно использовать для определения коэффициентов прогнозной модели.
Предположим, что у нас есть выборка из n наблюдений y1, y2,. . . , yn, которые можно рассматривать как реализации независимых пуассоновских случайных величин с Yi ∼ P (µi). Также предположим, что мы хотим, чтобы среднее значение µi (и, следовательно, дисперсия!) зависело от вектора независимых переменных xi. Мы могли бы сформировать простую линейную модель следующим образом:
где θ - вектор коэффициентов модели. Недостатком этой модели является то, что линейный предиктор в правой части может принимать любое действительное значение, тогда как среднее Пуассона в левой части, которое представляет ожидаемое количество, должно быть неотрицательным. Прямое решение этой проблемы - смоделировать логарифм среднего значения с помощью линейной модели. Таким образом, мы рассматриваем обобщенную линейную модель с логарифмами, которую можно записать следующим образом:
Наша цель - найти θ с помощью MLE.
Теперь распределение Пуассона определяется следующим образом:
Мы можем применить концепцию логарифмического правдоподобия, которую мы узнали в предыдущем разделе, чтобы найти θ. Взяв логарифм вышеуказанного уравнения и игнорируя константу, включающую log (y!), мы обнаруживаем, что функция логарифма правдоподобия:
где µi зависит от ковариации xi и вектора коэффициентов θ. Мы можем подставить µi = exp (xi’θ) и решить уравнение, чтобы получить θ, которое максимизирует правдоподобие. Когда у нас есть вектор θ, мы можем предсказать ожидаемое значение среднего, умножив вектор xi и θ.
MLE с помощью R
В этом разделе мы будем использовать набор реальных данных для решения проблемы, используя концепции, изученные ранее. Вы можете скачать набор данных по этой ссылке. Пример из набора данных выглядит следующим образом:
Datetime Count of tickets sold
25-08-2012 00:00 8
25-08-2012 01:00 2
25-08-2012 02:00 6
25-08-2012 03:00 2
25-08-2012 04:00 2
25-08-2012 05:00 2
Он подсчитывает количество билетов, проданных за каждый час с 25 августа 2012 г. по 25 сентября 2014 г. (около 18 000 записей). Наша цель - предсказать количество билетов, проданных за каждый час. Это тот же набор данных, который обсуждался в первом разделе этой статьи.
Проблема может быть решена с использованием таких методов, как регрессия, временные ряды и т. д. Здесь мы будем использовать метод статистического моделирования, который мы изучили выше, используя R.
Давайте сначала проанализируем данные. В статистическом моделировании нас больше интересует, как распределяется целевая переменная. Давайте посмотрим на распределение счетчиков:
hist(Y$Count, breaks = 50,probability = T ,main = "Histogram of Count Variable") lines(density(Y$Count), col="red", lwd=2)
Это можно рассматривать как распределение Пуассона, или мы могли бы даже попытаться подобрать экспоненциальное распределение.
Поскольку рассматриваемая переменная - это количество билетов, Пуассон - более подходящая модель для нее. Экспоненциальное распределение обычно используется для моделирования временного интервала между событиями.
Построим график количества проданных билетов за эти 2 года:
Похоже, что со временем продажи билетов значительно увеличатся. Чтобы не усложнять задачу, давайте смоделируем результат, используя в качестве фактора только возраст, где возраст определяется как количество недель, прошедших с 25 августа 2012 г. Мы можем записать это как:
где предполагается, что µ (количество проданных билетов) соответствует среднему значению распределения Пуассона, а θ0 и θ1 - это коэффициенты, которые нам необходимо оценить.
Комбинируя уравнения 1 и 2, мы получаем логарифмическую функцию правдоподобия следующим образом:
Мы можем использовать функцию mle() в пакете R stats4 для оценки коэффициентов θ0 и θ1. Ей необходимы следующие основные параметры:
- Функция отрицательного правдоподобия, которую необходимо минимизировать: она такая же, как и та, которую мы только что вывели, но с отрицательным знаком впереди [поскольку максимизация логарифмического правдоподобия - это то же самое, что минимизация отрицательного логарифмического правдоподобия]
- Начальная точка для вектора коэффициентов: это первоначальное предположение для коэффициента. Результаты могут варьироваться в зависимости от этих значений, поскольку функция может достигать локальных минимумов. Следовательно, полезно проверить результаты, запустив функцию с разными начальными точками.
- Необязательно указывается метод, с помощью которого следует оптимизировать функцию правдоподобия. BFGS - метод по умолчанию
В нашем примере отрицательная логарифмическая функция правдоподобия может быть закодирована следующим образом:
nll = function(theta0,theta1) {
x = Y$age[-idx]
y = Y$Count[-idx]
mu = exp(theta0 + x*theta1)
-sum(y*(log(mu)) - mu)
}Я разделил данные на обучающий и тестовый набор, чтобы мы могли объективно оценить эффективность модели. idx - это индексы строк, находящихся в тестовом наборе.
set.seed(200) idx = createDataPartition(Y$Count, p=0.25,list=FALSE)
Затем давайте вызовем функцию mle, чтобы получить параметры:
est = stats4::mle(minuslog=nll, start=list(theta0=2,theta1=0)) summary(est) Maximum likelihood estimation Call: stats4::mle(minuslogl = nll, start = list(theta0 = 2, theta1 = 0)) Coefficients: Estimate Std. Error theta0 2.68280754 2.548367e-03 theta1 0.03264451 2.998218e-05 -2 log L: -16594396
Это дает нам оценку коэффициентов. Давайте использовать RMSE в качестве метрики оценки для получения результатов на тестовом наборе:
pred.ts = (exp(coef(est)['theta0'] + Y$age[idx]*coef(est)['theta1'] )) rmse(pred.ts, Y$Count[idx]) 86.95227
Теперь давайте посмотрим, как наша модель соотносится со стандартной линейной моделью (с нормально распределенными ошибками), смоделированной с помощью логарифма count.
lm.fit = lm(log(Count)~age, data=Y[-idx,]) Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1.9112992 0.0110972 172.2 <2e-16 *** age 0.0414107 0.0001768 234.3 <2e-16 ***
pred.lm = predict(lm.fit, Y[idx,]) rmse(exp(pred.lm), Y$Count[idx]) 93.77393
Как видите, RMSE для стандартной линейной модели выше, чем у нашей модели с распределением Пуассона. Давайте сравним графики остатков для этих двух моделей на взятой выборке, чтобы увидеть, как модели работают в разных областях:
Мы видим, что ошибки с использованием регрессии Пуассона намного ближе к нулю по сравнению с нормальной линейной регрессией.
Подобного можно добиться в Python, используя функцию scipy.optimize.minimize(), которая принимает целевую функцию для минимизации, первоначальное предположение для параметров и методы, таких как BFGS, L-BFGS и т. д.
Еще проще смоделировать популярные распределения в R с помощью функции glm из пакета stats. Она поддерживает пуассоновское, гамма, биномиальное, квази, обратное гауссовское, квазибиномиальное, квазипуассоновское распределения из коробки. В примере, показанном выше, вы можете получить коэффициенты напрямую, используя следующую команду:
glm(Count ~ age, family = "poisson", data = Y) Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 2.669 2.218e-03 1203 <2e-16 *** age 0.03278 2.612e-05 1255 <2e-16 ***
То же самое можно сделать в Python, используя pymc.glm() и задав семейство pm.glm.families.Poisson().
Заключение
Один выводов о приведенном выше примере - это то, что существуют лучшие коэффициенты в пространстве параметров, чем те, которые оцениваются стандартной линейной моделью. Нормальное распределение является стандартной и наиболее широко используемой формой распределения, но мы можем получить лучшие результаты, если вместо этого использовать правильное распределение. Оценка максимального правдоподобия - это метод, который можно использовать для оценки параметров независимо от используемого распределения. Так что в следующий раз, когда у вас возникнет проблема моделирования, сначала посмотрите на распределение данных и посмотрите, есть ли смысл в чем-то отличном от нормального!
Подробный код и данные есть в моем репозитории Github. Обратитесь к файлу «Modelling single variables.R» за примером, который охватывает чтение, форматирование и моделирование данных с использованием только переменных age. Я также смоделировал процесс с использованием нескольких переменных, который представлен в файле «Modelling multiple variables.R».















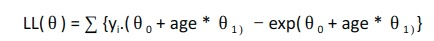


Комментариев нет:
Отправить комментарий