Введение
Любой алгоритм машинного обучения лучше всего работает в определенных условиях. Нельзя использовать алгоритм без учета условий. Например, если вы попробуете использовать линейную регрессию с факторными переменными, ничего хорошего из этого не получится.
Вместо этого в таких ситуациях лучше использовать такие алгоритмы, как логистическая регрессия, деревья решений, SVM, Random Forest и т.д.
В этой статье мы дадим вам полезные знания о логистической регрессии в R. После того, как вы освоили линейную регрессию, это будет естественным следующим шагом в вашем путешествии. Логистическую регрессию легко изучить и реализовать, но вы должны понимать принципы, лежащие в основе этого алгоритма. Я попытаюсь объяснить эти понятия простейшим способом. Давайте начнем.
Что такое логистическая регрессия?
Логистическая регрессия - алгоритм классификации. Он используется для прогнозирования двоичного результата (1/0, Да/Нет, True/False) для заданного набора независимых переменных. Чтобы представить двоичный/категориальный результат, мы используем фиктивные переменные. Вы можете также думать о логистической регрессии как о специальном случае линейной регрессии, когда результат в факторной форме, и мы используем логарифм коэффициентов в качестве зависимой переменной. Говоря простыми словами, она прогнозирует вероятность появления события путем подбора данных для функции logit.
Вывод уравнения логистической регрессии
Логистическая регрессия является частью более широкого класса алгоритмов, известных как обобщенная линейная модель (glm). В 1972 году Nelder и Wedderburn предложили эту модель для обеспечения возможности использования линейной регрессии в решении проблем, которые нельзя было напрямую решить с помощью линейной регрессии. Фактически они предложили класс различных моделей (линейная регрессия, ANOVA, регрессия Пуассона и т. д.), которые включали логическую регрессию как особый случай.
Фундаментальное уравнение обобщенной линейной модели имеет вид:
g(E(y)) = α + βx1 + γx2
Здесь g () - функция связи, E (y) - ожидаемое значение целевой переменной, а α + βx1 + γx2 - линейный предиктор (α, β, γ прогнозируются). Роль функции связи заключается в том, чтобы «связать» ожидаемые значения y с линейным предиктором.
Важные моменты
GLM не предполагает линейной зависимости между зависимыми и независимыми переменными. Однако она предполагает линейную зависимость между функцией связи и независимыми переменными в модели logit.
Зависимая переменная не обязательно должна быть нормально распределенной.
Для оценки параметров не используется метод наименьших квадратов (OLS). Вместо этого используется оценка максимального правдоподобия (MLE).
Ошибки должны быть независимыми, но не распределенными нормально.
Давайте рассмотрим пример:
У нас есть выборка из 1000 клиентов. Нам нужно предсказать вероятность того, покупает (y) ли клиент определенный журнал, или нет. Как вы можете видеть, у нас есть факторная переменная результата, поэтому мы будем использовать логистическую регрессию.
Чтобы начать с логистической регрессии, я сначала напишу простое уравнение линейной регрессии с зависимой переменной, заключенной в функцию связи:
g(y) = βo + β(Age) ---- (a)
Примечание. Для простоты я считаю «Age» независимой переменной.
В логистической регрессии нам нужна только вероятность исхода зависимой переменной (успех или неудача). Как было описано выше, g() является функцией связи. Эта функция задается с помощью двух вещей: вероятности успеха (p) и вероятности отказа (1-p). p должно соответствовать следующим критериям:
- оно всегда должно быть положительным (так как p> = 0);
- оно всегда должен быть меньше 1 (так как p <= 1).
Теперь мы просто воспользуемся этими двумя условиями и перейдем к сути логистической регрессии. Чтобы задать функцию связи, мы сначала обозначим g() с «p» и, в конечном итоге, выведем эту функцию.
Так как вероятность всегда должна быть положительной, мы преобразуем линейное уравнение в экспоненциальную форму. Для любого значения угла наклона и зависимой переменной экспонента в этом уравнении никогда не будет отрицательной.
p = exp(βo + β(Age)) = e^(βo + β(Age)) ------- (b)
Чтобы сделать вероятность меньше 1, мы должны разделить p на число, большее, чем p. Это просто:
p = exp(βo + β(Age)) / exp(βo + β(Age)) + 1 = e^(βo + β(Age)) / e^(βo + β(Age)) + 1 ----- (c)
Используя (a), (b) и (c), мы можем переопределить вероятность следующим образом:
p = e^y/ 1 + e^y --- (d)
где p - вероятность успешного исхода. (d) является Logit-функцией.
Если p - вероятность успешного исхода, 1-p будет вероятностью неудачного исхода, которая может быть записана как:
q = 1 - p = 1 - (e^y/ 1 + e^y) --- (e)
где q - вероятность неудачного исхода.
log (p/1-p) - функция связи. Логарифмическое преобразование результирующей переменной позволяет моделировать нелинейную связь линейным образом.
Подставляя значения y, мы получим:
Это уравнение, используемое в логистической регрессии. Здесь (p/1-p) - отношение шансов. Всякий раз, когда логарифм отношения шансов оказывается положительным, вероятность успешного исхода превышает 50%. Типичный график логистической модели показан ниже. Вы можете видеть, что вероятность всегда остается в диапазоне от 0 до 1.
Эффективность логистической регрессии
Для оценки эффективности модели логистической регрессии, мы должны рассмотреть несколько показателей. Независимо от инструмента (SAS, R, Python), с которым вы будете работать, всегда используйте следующие показатели:
1. AIC (Akaike Information Criteria). Аналогом R² в логистической регрессии является AIC. AIC - это мера соответствия, которая штрафует за использование излишнего количества параметров модели. Поэтому мы всегда предпочитаем модель с минимальным значением AIC.
2. Null Deviance и Residual Deviance - Null Deviance указывает на отклонение модели без параметров, только со свободным коэффициентом. Чем меньше значение, тем лучше модель. Residual Deviance указывает указывает на отклонение модели при добавлении независимых переменных. Чем меньше значение, тем лучше модель.
3. Матрица ошибок (Confusion Matrix): это не что иное, как табличное представление фактических и прогнозируемых значений. Она помогает нам оценить точность модели и избежать переобучения. Вот как она выглядит:
Вы можете рассчитать точность вашей модели следующим образом:
Из матрицы ошибок можно найти чувствительность специфичность (Specificity) и чувствительность (Sensitivity), которые определяются следующим образом:
Специфичность и чувствительность играют критичную роль в определении ROC-кривой.
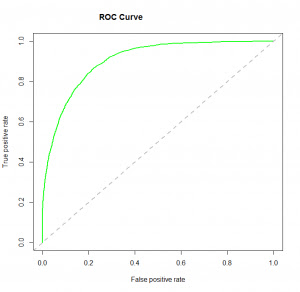
4. ROC-кривая (Receiver Operating Characteristic) суммирует эффективность модели, оценивая компромисс между TPR (чувствительностью) и FPR (1- специфичность). Для построения ROC рекомендуется принять p> 0,5, так как нас больше интересует вероятность успеха. ROC суммирует предсказательную силу для всех возможных значений при p> 0,5. Площадь под кривой (AUC), называемая индексом точности (A) или индексом согласованности, является идеальной метрикой эффективности для ROC-кривой. Чем больше область под кривой, тем лучше предсказательная сила модели. Ниже приведен образец ROC-кривой. ROC идеальной предсказательной модели имеет TP, равное 1, а FP равное 0. Эта кривая будет касаться верхнего левого угла графика.
Примечание. Для оценки эффективности модели вы также можете использовать функцию правдоподобия. Она называется так, потому что выбирает значения коэффициентов, которые максимизируют вероятность объяснения наблюдаемых данных. Она указывает на хорошее соответствие, если ее значение приближается к одному, и плохое соответствие данных, если ее значение приближается к нулю.
Модель логистической регрессии в R
Для правдоподобности я строил модель на практической проблеме - наборе данных Dressify. Вы можете скачать его здесь. Не углубляясь в дебри, ниже приведен сценарий построения простой модели логистической регрессии:
setwd('C:/Users/manish/Desktop/dressdata')#load data
train <- read.csv('Train_Old.csv')#create training and validation data from given data
install.packages('caTools')
library(caTools)set.seed(88) split <- sample.split(train$Recommended, SplitRatio = 0.75)
#get training and test data dresstrain <- subset(train, split == TRUE) dresstest <- subset(train, split == FALSE)
#logistic regression model model <- glm (Recommended ~ .-ID, data = dresstrain, family = binomial) summary(model)
predict <- predict(model, type = 'response')
#confusion matrix table(dresstrain$Recommended, predict > 0.5)
#ROCR Curve library(ROCR) ROCRpred <- prediction(predict, dresstrain$Recommended) ROCRperf <- performance(ROCRpred, 'tpr','fpr') plot(ROCRperf, colorize = TRUE, text.adj = c(-0.2,1.7))
#plot glm library(ggplot2) ggplot(dresstrain, aes(x=Rating, y=Recommended)) + geom_point() + stat_smooth(method="glm", family="binomial", se=FALSE)
Эти данные требуют хорошей чистки и дополнительной подготовки. Объем этой статьи ограничивает меня построением модели логистической регрессии. Я бы рекомендовал вам поработать над этой проблемой самостоятельно. Здесь есть чему поучиться.
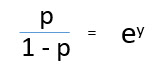






Комментариев нет:
Отправить комментарий