7 способов прогнозирования временных рядов с помощью Python

Перевод. Оригинал: 7 methods to perform Time Series forecasting (with Python codes)

Введение

Большинство из вас слышало о новом веянии на рынке, то есть криптовалюте. Многие может быть вложили бы деньги в них. Но безопасно ли инвестировать деньги в такую изменчивую валюту? Как мы можем быть уверены, что инвестирование в криптовалюту сейчас принесет прибыль в будущем? Мы не можем быть уверены, но мы можем сгенерировать прогнозы на основе предыдущих цен. Модели временных рядов - один из способов их прогнозирования.

Помимо криптовалют, есть несколько важных областей, в которых используется прогнозирование временных рядов, например: прогнозирование продаж, количество звонков в колл-центре, солнечная активность, приливы, поведение активов на фондовом рынке и многое другое.

Предположим, что менеджер отеля хочет предсказать, сколько посетителей он должен ожидать в следующем году, чтобы соответственно скорректировать запасы отеля и сделать разумное предположение о доходах отеля. Основываясь на данных предыдущих лет/месяцев/дней, он может использовать прогнозирование временных рядов и получить приблизительное количество посетителей. 

В этой статье мы узнаем о разных методах прогнозирования и сравним их с помощью одного набора данных. Мы рассмотрим различные методы и посмотрим, как использовать эти методы для улучшения результатов.

Набор данных можно также скачать здесь.

Давайте начнем!

Постановка задачи и набор данных

Мы рассмотрим проблему, связанную с прогнозированием количества пассажиров JetRail, нового высокоскоростного железнодорожного сервиса от Unicorn Investors. Нам предоставляются данные за 2 года (август 2012 г. - сентябрь 2014 г.), и с помощью этих данных мы должны прогнозировать количество пассажиров на ближайшие 7 месяцев.

Давайте начнем работать с набором данных, загруженным по вышеуказанной ссылке. В этой статье я работаю только с набором данных train.

import pandas as pd 

import numpy as np 

import matplotlib.pyplot as plt 

# импорт данных

df = pd.read_csv('train.csv')

df.head()

df.tail()

Как можно видеть, мы получаем часовые данные за 2 года (2012–2014 годы) с количеством путешествующих пассажиров, и нам необходимо оценить количество пассажиров в будущем.

В этой статье я разбираю и объединяю наборы данных, чтобы объяснить различные методики.

Подмножество набора данных (август 2012 г. - декабрь 2013 г.)

Агрегирование набора данных на ежедневной основе

Создание обучающего и тестового файла для моделирования. Первые 14 месяцев (август 2012 г. - октябрь 2013 г.) используются в качестве данных для обучения, а следующие 2 месяца (ноябрь 2013 г. - декабрь 2013 г.) - данные для тестирования.

#Выбираем поддиапазон данных

#Index 11856 указывает на конец 2013 года

df = pd.read_csv('train.csv', nrows = 11856)

#Создание обучающего и тестового наборов

#Индекс 10392 указывает на конец октября 2013 года

train=df[0:10392]

test=df[10392:]

# Агрегирование набора данных на ежедневной основе

df.Timestamp = pd.to_datetime(df.Datetime,format='%d-%m-%Y %H:%M') 

df.index = df.Timestamp 

df = df.resample('D').mean()

train.Timestamp = pd.to_datetime(train.Datetime,format='%d-%m-%Y %H:%M') 

train.index = train.Timestamp 

train = train.resample('D').mean() 

test.Timestamp = pd.to_datetime(test.Datetime,format='%d-%m-%Y %H:%M') 

test.index = test.Timestamp 

test = test.resample('D').mean()

Давайте визуализируем данные (обучающие и тестовые вместе), чтобы знать, как они меняются в течение определенного периода времени.

#Строим график

train.Count.plot(figsize=(15,8), title= 'Daily Ridership', fontsize=14)

test.Count.plot(figsize=(15,8), title= 'Daily Ridership', fontsize=14)

plt.show()

Установка библиотеки (statsmodels)

Библиотека, которую я использовал для прогнозирования временных рядов, - statsmodels. Вам необходимо установить ее, прежде чем применять несколько из указанных ниже подходов. Возможно, statsmodels уже установлена в вашей среде Python, но она не поддерживает методы прогнозирования. Мы будем клонировать ее из своего репозитория и установим с использованием исходного кода. Следуй этим шагам:

1. Используйте команду pip freeze, чтобы проверить, установлена ли она уже в вашей среде.
2. Если она уже есть, удалите ее, используя команду «conda remove statsmodels».
3. Клонируйте репозиторий statsmodels, используя команду «git clone git: //github.com/statsmodels/statsmodels.git». Инициализируйте Git, используя команду «git init» перед клонированием.
4. Измените каталог на statsmodels с помощью команды «cd statsmodels».
5. Создайте установочный файл с помощью команды «python setup.py build».
6. Установите его с помощью команды «python setup.py install».
7. Выйдите из терминала.
8. Перезапустите терминал в вашей среде, откройте python и выполните команду «from statsmodels.tsa.api import ExponentialSmoothing» для проверки.

Метод 1: начинаем с наивного подхода

Рассмотрим график, приведенный ниже. Предположим, что ось Y отображает цену монеты, а ось X - время (дни).

Из графика можно сделать вывод, что цена монеты стабильна с самого начала. Часто нам предоставляется набор данных, который стабилен в течение всего периода времени. Если мы хотим прогнозировать цену на следующий день, мы можем просто взять значение последнего дня и предположить, что то же значение будет и на следующий день. Такой метод прогнозирования, который предполагает, что следующая ожидаемая точка равна последней наблюдаемой точке, называется наивным методом.

Теперь мы будем реализовывать наивный метод  для прогнозирования цен на тестовых данных.

dd= np.asarray(df.Count)

y_hat = test.copy()

y_hat['naive'] = dd[len(dd)-1]

plt.figure(figsize=(12,8))

plt.plot(train.index, train['Count'], label='Train')

plt.plot(test.index,test['Count'], label='Test')

plt.plot(y_hat.index,y_hat['naive'], label='Naive Forecast')

plt.legend(loc='best')

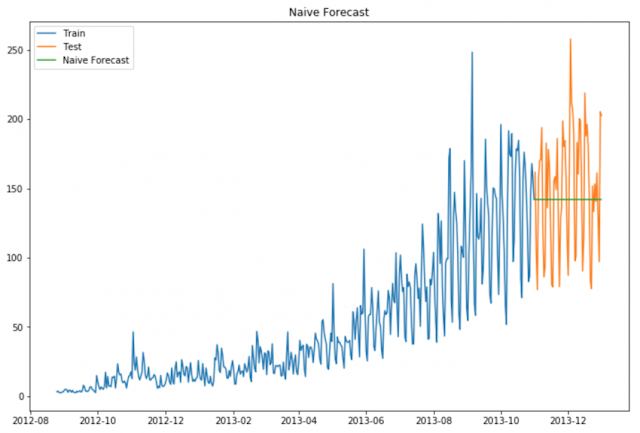
plt.title("Naive Forecast")

plt.show()

Теперь мы рассчитаем среднеквадратичную ошибку (RMSE), чтобы проверить точность нашей модели на тестовых данных.

from sklearn.metrics import mean_squared_error

from math import sqrt

rms = sqrt(mean_squared_error(test.Count, y_hat.naive))

print(rms)

RMSE = 43.9164061439

Из значения RMSE и приведенного выше графика можно сделать вывод, что наивный метод не подходит для наборов данных с высокой изменчивостью. Лучше всего он подходит для стабильных наборов данных. Теперь мы рассмотрим другую технику и попытаемся улучшить наш результат.

Метод 2. Простое среднее.

Рассмотрим график, приведенный ниже. Предположим, что ось Y отображает цену монеты, а ось X - время (дни).

Из графика можно сделать вывод, что цена монеты увеличивается и уменьшается случайным образом с небольшим диапазоном, так что среднее значение остается постоянным. Нам предоставляется набор данных, который хотя и изменяется с небольшим диапазоном колебаний на протяжении всего периода времени, но среднее значение для каждого периода времени остается постоянным. В таком случае мы можем прогнозировать цену следующего дня как  аналогичную средней за все прошедшие дни.

Такой метод прогнозирования, который прогнозирует ожидаемое значение, равное среднему значению всех ранее наблюдаемых точек, называется методом простого среднего.

Мы берем все ранее известные значения, вычисляем среднее значение и принимаем его как следующее значение. Конечно, это не будет точным попаданием, но достаточно близким. На самом деле бывают ситуации, когда этот метод работает лучше всего.

y_hat_avg = test.copy()

y_hat_avg['avg_forecast'] = train['Count'].mean()

plt.figure(figsize=(12,8))

plt.plot(train['Count'], label='Train')

plt.plot(test['Count'], label='Test')

plt.plot(y_hat_avg['avg_forecast'], label='Average Forecast')

plt.legend(loc='best')

plt.show()

Теперь мы рассчитаем RMSE, чтобы проверить точность нашей модели.

rms = sqrt(mean_squared_error(test.Count, y_hat_avg.avg_forecast))

print(rms)

RMSE = 109.545990803

Мы видим, что эта модель не улучшила нашу оценку. Следовательно, можно сделать вывод, что этот метод работает лучше всего, когда среднее значение за каждый период времени остается постоянным. Хотя наивный метод лучше, чем метод простого среднего, это не означает, что наивный метод лучше простого среднего для всех наборов данных. 

Метод 3. Скользящее среднее.

Рассмотрим график, приведенный ниже. Предположим, что ось Y отображает достоинство монеты, а ось X - время (дни).

Из графика можно сделать вывод, что достоинство монеты несколько раз увеличивалось некоторое время назад в большом диапазоне, но теперь оно стабильно. Нам предоставляется набор данных, в котором цены/продажи объекта несколько увеличились/резко снизились несколько периодов назад. Чтобы использовать предыдущий метод среднего, мы должны использовать среднее значение всех предыдущих данных, но использование всех предыдущих данных не кажется правильным.

Использование цен начального периода сильно повлияет на прогноз на следующий период. Поэтому в качестве улучшения по сравнению с простым средним мы возьмем среднее значение цен только за последние несколько периодов времени. Очевидно, что мысль здесь заключается в том, что важны только последние цены. Такая методика прогнозирования, которая использует период времени для расчета среднего, называется методикой скользящего среднего. Расчет скользящего среднего включает то, что иногда называют «скользящим окном» размера n.

Используя простую модель скользящего среднего, мы прогнозируем следующее значение (s) во временном ряду на основе среднего значения фиксированного конечного числа «p» предыдущих значений. Таким образом, для всех i > p

Скользящая средняя на самом деле может быть довольно эффективной, особенно если вы выберете правильное значение p для ряда.

y_hat_avg = test.copy()

y_hat_avg['moving_avg_forecast']=train['Count'].rolling(60).mean().iloc[-1]

plt.figure(figsize=(16,8))

plt.plot(train['Count'], label='Train')

plt.plot(test['Count'], label='Test')

plt.plot(y_hat_avg['moving_avg_forecast'], label='Moving Average Forecast')

plt.legend(loc='best')

plt.show()

Мы выбрали данные только за последние 2 месяца. Теперь мы рассчитаем RMSE, чтобы проверить точность нашей модели.

rms=sqrt(mean_squared_error(test.Count, y_hat_avg.moving_avg_forecast))

print(rms)

RMSE = 46.7284072511

Мы видим, что наивный метод превосходит как метод простого среднего, так и метод скользящего среднего для этого набора данных. Теперь мы рассмотрим метод простого экспоненциального сглаживания и посмотрим, как он работает.

Дальнейшее развитие метода скользящей средней - метод взвешенной скользящей средней. В методе скользящего среднего, как показано выше, мы одинаково взвешиваем прошлые «n» наблюдений. Но мы можем столкнуться с ситуациями, когда каждое из наблюдений из «n» значений по-своему влияет на прогноз. Такой метод, который по-разному взвешивает прошлые наблюдения, называется методом взвешенного скользящего среднего.

Взвешенное скользящее среднее - это скользящее среднее, в котором значениям скользящего окна присваиваются разные веса, как правило, так что более свежие точки имеют большее значение. Вместо выбора размера окна требуется список весов (которые в сумме должны составлять до 1). 

Например, если мы выберем [0,40, 0,25, 0,20, 0,15] в качестве весов, мы дадим 40%, 25%, 20% и 15% последним 4 точкам соответственно.

Метод 4 – простое экспоненциальное сглаживание

Поняв вышеописанные методы, мы можем заметить, что простое среднее и взвешенное скользящее среднее лежат на совершенно противоположных концах. Нам нужно что-то между этими двумя крайними подходами, которое учитывает все данные при различном взвешивании точек данных. Например, может быть целесообразно придать больший вес более поздним наблюдениям, чем наблюдениям из далекого прошлого. Техника, которая работает по этому принципу, называется простым экспоненциальным сглаживанием. Прогнозы рассчитываются с использованием средневзвешенных значений, в которых веса экспоненциально уменьшаются по мере того, как наблюдения уходят в прошлое, наименьшие веса связаны с самыми старыми наблюдениями:

где 0≤ α ≤1 - параметр сглаживания.

Прогноз на один шаг вперед для времени T + 1 является средневзвешенным значением всех наблюдений в серии y1,…, yT. Скорость, с которой снижаются веса, определяется параметром α.

Если вы посмотрите на него достаточно долго, вы увидите, что ожидаемое значение ŷx является суммой двух произведений: α⋅yt и (1 − α) ⋅ŷ t-1.

Следовательно, это также может быть записано как:

По сути, мы получили взвешенное скользящее среднее с двумя весами: α и 1 − α.

Как мы видим, 1 − α умножается на предыдущее ожидаемое значение ŷ x − 1, что делает выражение рекурсивным. И именно поэтому этот метод называется экспоненциальным. Прогноз в момент времени t + 1 равен средневзвешенному значению между самым последним наблюдением yt и самым последним прогнозом ŷ t | t − 1.

from statsmodels.tsa.api import ExponentialSmoothing, SimpleExpSmoothing, Holt

y_hat_avg = test.copy()

fit2=SimpleExpSmoothing(np.asarray(train['Count'])).fit(smoothing_level=0.6,optimized=False)

y_hat_avg['SES'] = fit2.forecast(len(test))

plt.figure(figsize=(16,8))

plt.plot(train['Count'], label='Train')

plt.plot(test['Count'], label='Test')

plt.plot(y_hat_avg['SES'], label='SES')

plt.legend(loc='best')

plt.show()

Теперь мы рассчитаем RMSE, чтобы проверить точность нашей модели.

rms = sqrt(mean_squared_error(test.Count, y_hat_avg.SES))

print(rms)

RMSE = 43.3576252252

Мы можем видеть, что реализация простой экспоненциальной модели с альфа 0,6 генерирует наиболее точный прогноз из всех, рассмотренных ранее. Мы можем настроить параметр, используя проверочный набор данных, чтобы сгенерировать еще более лучшую простую экспоненциальную модель.

Метод 5 –  метод линейного тренда Холта

Теперь мы изучили несколько методов прогнозирования, но мы видим, что эти модели плохо работают с данными с большими колебаниями. Предположим, что цена биткойна растет.

Если мы используем любой из вышеперечисленных методов, он не будет учитывать эту тенденцию. Тренд - это общая картина цен, которую мы наблюдаем в течение определенного периода времени. В этом случае мы видим, что существует тенденция к увеличению.

Хотя каждый из этих методов может быть применен и к тренду. Например, наивный метод предполагает, что тренд между двумя последними точками останется прежним, или мы могли бы усреднить все наклоны между всеми точками, чтобы получить средний тренд, использовать скользящее среднее тренда или применить экспоненциальное сглаживание.

Но нам нужен метод, который может точно отображать тренд без каких-либо предположений. Такой метод, который учитывает тренд набора данных, называется методом линейного тренда Холта.

Каждый набор данных временного ряда может быть разложен на составляющие: тренд, сезонность и остаток. Любой набор данных, который следует за трендом, может использовать метод линейного тренда Холта для прогнозирования.

import statsmodels.api as sm

sm.tsa.seasonal_decompose(train.Count).plot()

result = sm.tsa.stattools.adfuller(train.Count)

plt.show()

Из полученных графиков видно, что этому набору данных соответствует растущий тренд. Следовательно, мы можем использовать линейный тренд Холта для прогнозирования будущих цен.

Холт расширил простое экспоненциальное сглаживание, чтобы позволить прогнозировать данные с трендом. Это не более чем экспоненциальное сглаживание, применяемое как к уровню (среднее значение в ряду), так и к тренду. Чтобы выразить это в математической записи, нам теперь нужно три уравнения: одно для уровня, одно для тренда и одно для объединения уровня и тренда, чтобы получить ожидаемый прогноз.

Значения, которые мы предсказали в вышеупомянутых алгоритмах, называются Уровнем. В приведенных выше трех уравнениях вы можете заметить, что мы добавили уровень и тренд для создания уравнения прогноза.

Как и в случае простого экспоненциального сглаживания, уравнение уровня здесь показывает, что оно представляет собой средневзвешенное значение наблюдения и прогноз на один шаг впереди выборки. Уравнение тренда показывает, что оно представляет собой средневзвешенное значение оценочного тренда в момент времени t на основе ℓ (t) −ℓ (t − 1) и b (t − 1), предыдущей оценки тренда.

Мы добавим эти уравнения, чтобы сгенерировать уравнение прогноза. Мы также можем сгенерировать мультипликативное уравнение прогноза, умножив тренд и уровень вместо сложения. Когда тренд растет или падает линейно, используется аддитивное уравнение, когда тренд растет или падает экспоненциально, используется мультипликативное уравнение. Практика показывает, что умножение является более устойчивым предиктором, однако аддитивный метод проще понять.

y_hat_avg = test.copy()

fit1=Holt(np.asarray(train['Count'])).fit(smoothing_level=0.3,smoothing_slope = 0.1)

y_hat_avg['Holt_linear'] = fit1.forecast(len(test))

plt.figure(figsize=(16,8))

plt.plot(train['Count'], label='Train')

plt.plot(test['Count'], label='Test')

plt.plot(y_hat_avg['Holt_linear'], label='Holt_linear')

plt.legend(loc='best')

plt.show()

Теперь мы рассчитаем RMSE, чтобы проверить точность нашей модели.

rms = sqrt(mean_squared_error(test.Count, y_hat_avg.Holt_linear))

print(rms)

RMSE = 43.0562596115

Мы видим, что этот метод точно отображает тренд и, следовательно, обеспечивает лучшее решение по сравнению с рассмотренными ранее моделями. Мы также можем настроить параметры, чтобы получить еще более точную модель.

Метод 6 – Метод Холта-Винтера

Итак, давайте введем новый термин, который будет использоваться в этом алгоритме. Рассмотрим отель, расположенный в горах. У него много посетителей в течение летнего сезона, тогда как посетителей в остальное время года намного меньше. Следовательно, прибыль, полученная владельцем, будет намного больше в летний сезон, по сравнению с любым другим сезоном. Эта картина будет повторяться каждый год. Такое повторение называется сезонностью. Наборы данных, которые показывают подобный набор паттернов через фиксированные интервалы времени, страдают от сезонности.

Рассмотренные ранее модели не учитывают сезонность набора данных при прогнозировании. Следовательно, нам нужен метод, который учитывает как тренд, так и сезонность для прогнозирования будущих цен. Одним из таких алгоритмов, который мы можем использовать в таком сценарии, является метод Холта-Винтера. Идея тройного экспоненциального сглаживания заключается в применении экспоненциального сглаживания к сезонным компонентам в дополнение к уровню и тренду.

Метод Холта-Винтера будет лучшим вариантом среди остальных моделей из-за сезонности. Сезонный метод Холта-Винтера включает в себя уравнение прогноза и три уравнения сглаживания - одно для уровня ℓt, одно для тренда bt и одно для сезонной компоненты, обозначенной st, с параметрами сглаживания α, β и γ.

где s - длина сезонного цикла, для 0 ≤ α ≤ 1, 0 ≤ β ≤ 1 и 0 ≤ γ ≤ 1.

Уравнение уровня показывает средневзвешенное значение между сезонно скорректированным наблюдением и несезонным прогнозом для времени t. Уравнение тренда идентично линейному методу Холта. Сезонное уравнение показывает средневзвешенное значение между текущим сезонным индексом и сезонным индексом того же сезона в прошлом году (т.е. периоды времени назад).

В этом методе мы также можем реализовать как аддитивную, так и мультипликативную технику. Аддитивный метод предпочтителен, когда сезонные колебания примерно постоянны по всему ряду, в то время как мультипликативный метод предпочтителен, когда сезонные колебания изменяются пропорционально уровню ряда.

y_hat_avg = test.copy()

fit1=ExponentialSmoothing(np.asarray(train['Count']) ,seasonal_periods=7 ,trend='add', seasonal='add',).fit()

y_hat_avg['Holt_Winter'] = fit1.forecast(len(test))

plt.figure(figsize=(16,8))

plt.plot( train['Count'], label='Train')

plt.plot(test['Count'], label='Test')

plt.plot(y_hat_avg['Holt_Winter'], label='Holt_Winter')

plt.legend(loc='best')

plt.show()

Теперь мы рассчитаем RMSE, чтобы проверить точность нашей модели.

rms = sqrt(mean_squared_error(test.Count, y_hat_avg.Holt_Winter))

print(rms)

RMSE = 23.9614925662

Из графика видно, что отображение правильного тренда и сезонности дает гораздо лучшее решение. Мы выбрали seasonal_period = 7, поскольку данные повторяются еженедельно. Другие параметры могут быть настроены в соответствии с набором данных. Я использовал параметры по умолчанию при построении этой модели. Вы можете настроить параметры для достижения лучшей точности.

Метод 7 – ARIMA

Еще одна распространенная модель временных рядов, которая очень популярна среди ученых, - это ARIMA. Это сокращение от "Autoregressive Integrated Moving average". В то время как модели экспоненциального сглаживания основывались на описании тренда и сезонности в данных, модели ARIMA стремятся описать корреляции в данных между собой. Улучшение по сравнению с ARIMA - это Seasonal ARIMA. Она учитывает сезонность набора данных так же, как метод Холта Винтера. Вы можете больше узнать о ARIMA и сезонных моделях ARIMA и о предварительной обработке данных из этих статей (1) и (2).

y_hat_avg = test.copy()

fit1=sm.tsa.statespace.SARIMAX(train.Count, order=(2, 1, 4),seasonal_order=(0,1,1,7)).fit()

y_hat_avg['SARIMA'] = fit1.predict(start="2013-11-1", end="2013-12-31", dynamic=True)

plt.figure(figsize=(16,8))

plt.plot( train['Count'], label='Train')

plt.plot(test['Count'], label='Test')

plt.plot(y_hat_avg['SARIMA'], label='SARIMA')

plt.legend(loc='best')

plt.show()

Теперь мы рассчитаем RMSE, чтобы проверить точность нашей модели.

rms = sqrt(mean_squared_error(test.Count, y_hat_avg.SARIMA))

print(rms)

RMSE = 26.035582877

Мы видим, что использование Seasonal ARIMA создает решение, похожее на метод Холта-Винтера. Мы выбрали параметры в соответствии с графиками ACF и PACF. Вы можете узнать о них больше  по ссылкам, указанным выше. Если вы сталкиваетесь с трудностями при поиске параметров модели ARIMA, вы можете использовать auto.arima, реализованный на языке R. Заменитель auto.arima в Python можно посмотреть здесь.

Мы можем сравнить эти модели на основе их баллов RMSE.

Заключение

Я надеюсь, что эта статья была полезна, и теперь вам будет проще решать подобные проблемы временных рядов. Я предлагаю вам попробовать различные виды постановок задач и не торопиться, чтобы решить их, используя вышеупомянутые методы. Попробуйте эти модели и посмотрите, какая модель лучше всего подходит для временных рядов.

Один из уроков, который можно извлечь из этой статьи, заключается в том, что каждая из этих моделей может превзойти другие на определенном наборе данных. Следовательно, это не означает, что одна модель, которая работает лучше всего для одного типа набора данных, будет выполнять то же самое для всех остальных.

Вы также можете изучить пакет forecast, созданный для моделирования временных рядов на языке R. Вы также можете изучить модели двойной сезонности из пакета forecast. Использование модели двойной сезонности в этом наборе данных позволит получить лучшую модель и, следовательно, лучший результат.