Полное руководство по исследованию данных

Перевод. Оригинал: A Comprehensive Guide to Data Exploration

Введение

Я работаю специалистом по бизнес-аналитике уже почти три года. В начале моей работы один из моих наставников советовал мне тратить больше времи на исследование и анализ данных. Следование его совету сослужило мне хорошую службу.

Я создал это руководство, чтобы помочь вам понять основные методы исследования данных. Как всегда, я старался изо всех сил объяснить эти понятия самым простым способом. Для лучшего понимания я привел несколько примеров, чтобы продемонстрировать сложные концепции.

Давайте начнем.

1. Этапы исследования и подготовки данных

Помните, что качество ваших входных данных определяет качество вашей продукции. Итак, как только вы подготовили свою бизнес-гипотезу, имеет смысл потратить много времени и усилий на исследование данных. По моим личным оценкам, исследование, очистка и подготовка данных могут занять до 70% от общего времени проекта.

Ниже приведены этапы, необходимые для понимания, очистки и подготовки ваших данных для построения вашей прогностической модели:

1. Идентификация переменных

2. Одномерный анализ

3. Двухвариантный анализ

4. Обработка отсутствующих значений

5. Обработка выбросов

6. Преобразование переменных

7. Конструирование признаков

Наконец, нам нужно будет повторить эти шаги 4–7 раз, прежде чем мы создадим нашу усовершенствованную модель.

Давайте теперь изучим каждый этап подробно:

Идентификация переменных

Сначала определите предиктор и целевую переменную. Затем определите тип данных и категорию переменных.

Давайте разберемся в этом шаге на примере.

Пример: предположим, мы хотим предсказать, будут ли студенты играть в крикет или нет (см. набор данных ниже). Здесь вам необходимо определить предикторы, целевую переменную, типы данных переменных и категорию переменных.

Ниже переменные были определены в другой категории:

Одномерный анализ

На этом этапе мы исследуем переменные одну за другой. Метод выполнения анализа переменной будет зависеть от того, является ли переменная категориальной или числовой. Давайте рассмотрим эти методы и статистические показатели для категориальных и числовых переменных в отдельности:

Числовые переменные: в случае числовых переменных нам необходимо понять центральную тенденцию и разброс переменной. Они измеряются с использованием различных методов визуализации статистических метрик, как показано ниже:

Примечание. Однофакторный анализ также используется для выделения отсутствующих значений и выбросов. В следующей части этой серии статей мы рассмотрим методы обработки пропущенных значений и выбросов. Чтобы узнать больше об этих методах, вы можете обратиться к курсу от Udacity.

Категориальные переменные. Для категориальных переменных мы будем использовать таблицу частот, чтобы понять распределение каждой категории. Мы также можем смотреть проценты от значений по каждой категории. Их можно измерить, используя две метрики: Count и Count% для каждой категории. В качестве визуализации может быть использована гистограмма.

Двухвариантный анализ

Двухвариантный анализ обнаруживает связь между двумя переменными. Здесь мы ищем связь между переменными на заданном уровне значимости. Мы можем выполнить двухвариантный анализ для любой комбинации категориальных и непрерывных переменных. Комбинации могут быть следующие: категориальная и категориальная, категориальная и непрерывная, непрерывная и непрерывная. Различные методы используются для решения этих комбинаций в процессе анализа.

Давайте разберемся в возможных комбинациях в деталях:

Непрерывная и непрерывная. Выполняя двухвариантный анализ для двух непрерывных переменных, мы должны смотреть на график рассеяния. Это отличный способ выяснить соотношения между двумя переменными. Паттерн графика указывает на связь между переменными. Отношения могут быть линейными или нелинейными.

График рассеяния показывает взаимосвязь между двумя переменными, но не указывает на силу взаимосвязи между ними. Чтобы найти силу взаимосвязей, мы используем корреляцию. Корреляция варьируется от -1 до +1.

-1: идеальная отрицательная линейная корреляция

+1: идеальная положительная линейная корреляция

0: нет корреляции

Корреляция может быть рассчитана с использованием следующей формулы:

Correlation = Covariance(X,Y) / SQRT( Var(X)* Var(Y))

Различные программные пакеты имеют функции или функциональность для определения корреляции между переменными. В Excel для возврата корреляции между двумя переменными используется функция CORREL(), а SAS использует для определения корреляции процедуру PROC CORR. Эта функция возвращает значение корреляции Пирсона:

В приведенном выше примере у нас хорошая положительная корреляция (0,65) между переменными X и Y.

Категориальные переменные: чтобы найти связь между двумя категориальными переменными, мы можем использовать следующие методы:

Таблица сопряженности: мы можем начать анализировать отношения, создав двустороннюю таблицу count и count%. Строки представляют категории одной переменной, а столбцы представляют категории другой переменной. Мы показываем количество или количество % наблюдений, доступных в каждой комбинации категорий строк и столбцов.

Столбчатая диаграмма с накоплением. Этот метод представляет собой скорее другую визуальную форму таблицы сопряженности.

Тест хи-квадрат: этот тест используется для определения статистической значимости взаимосвязи между переменными. Кроме того, он проверяет, достаточно ли убедительны данные в выборке, чтобы обобщить эту взаимосвязь и для большей популяции. Хи-квадрат основан на разнице между ожидаемой и наблюдаемой частотами в одной или нескольких категориях в таблице сопряженности. Возвращает вероятность для вычисленного распределения хи-квадрат с заданной степенью свободы.

Вероятность 0: указывает на то, что обе категориальные переменные являются зависимыми

Вероятность 1: показывает, что обе переменные являются независимыми.

Вероятность менее 0,05: это указывает на то, что связь между переменными является достоверной с уровнем достоверности 95%. Статистика теста хи-квадрат для проверки независимости двух категориальных переменных рассчитывается следующим образом:

где O представляет наблюдаемую частоту. E - ожидаемая частота при нулевой гипотезе и рассчитывается по формуле:

Из предыдущей таблицы сопряженности ожидаемое количество для категории 1, которое должно быть небольшого размера, составляет 0,22. Оно получается путем взятия итоговой суммы для размера (9), умноженной на общую сумму столбца для категории продукта (2), с последующим делением на размер выборки (81). Эта процедура проводится для каждой ячейки. Статистические меры, используемые для анализа силы отношений:

- V-коэффициент Крамера (Cramer’s V) для номинальной категориальной переменной;

- критерий Кохрана-Мантеля-Хензеля (Mantel-Haenszed Chi-Square) для порядковой категориальной переменной.

Различные языки и инструменты для обработки данных имеют специальные методы для выполнения теста хи-квадрат. В SAS мы можем использовать Chisq как опцию с Proc freq для выполнения этого теста.

Категориальные и непрерывные переменные: изучая связь между категориальными и непрерывными переменными, мы можем нарисовать коробочные графики для каждого уровня категориальных переменных. Если уровни малы по количеству, это не будет показывать статистическую значимость. Чтобы посмотреть статистическую значимость, мы можем выполнить Z-тест, T-тест или ANOVA.

Z-тест/T-тест: оценивает, являются ли средние значения двух групп статистически отличными друг от друга или нет. 

Чем меньше вероятность Z, тем более значимой будет разница двух средних. T-критерий очень похож на Z-критерий, но он используется, когда количество наблюдений для обеих категорий меньше 30.

ANOVA: оценивает, является ли среднее по более чем двум группам статистически различным.

Пример. Предположим, мы хотим проверить эффект пяти различных упражнений. Для этого мы набираем 20 мужчин и назначаем один из видов упражнений 4 мужчинам (5 групп). Их вес записывается через несколько недель. Нам необходимо выяснить, существенно ли отличается влияние этих упражнений на них или нет. Это можно сделать путем сравнения весов 5 групп по 4 человека в каждой.

До сих пор мы изучали первые три этапа: исследование данных, идентификация переменных, одномерный и двухвариантный анализ. Мы также рассмотрели различные статистические и визуальные методы для определения взаимосвязи между переменными.

Теперь рассмотрим методы обработки пропущенных значений. Что еще более важно, мы также посмотрим, почему в наших данных встречаются пропущенные значения, и почему их необходимо обрабатывать.

2. Обработка отсутствующих значений

Зачем требуется обработка пропущенных значений?

Отсутствие данных в наборе обучающих данных может снизить мощность/соответствие модели или привести к смещенной модели, потому что мы неправильно проанализировали поведение и отношения между переменными. Это может привести к неправильному прогнозу или классификации.

Обратите внимание на пропущенные значения на изображении, показанном выше: в левом сценарии мы не обработали пропущенные значения. Вывод из этого набора данных заключается в том, что шансы играть в крикет у мужчин выше, чем у женщин. С другой стороны, если вы посмотрите на вторую таблицу, в которой приведены данные после обработки пропущенных значений (в зависимости от пола), мы увидим, что у женщин больше шансов играть в крикет по сравнению с мужчинами.

Почему в моих данных есть отсутствующие значения?

Мы рассмотрели важность обработки пропущенных значений в наборе данных. Теперь давайте выясним причины появления этих пропущенных значений. Они могут появляться во время двух этапов:

Извлечение данных: возможно, существуют проблемы с процессом извлечения. В таких случаях мы должны перепроверить правильные данные совместно с хранилищем данных. Некоторые процедуры хеширования также можно использовать для проверки правильности извлечения данных. Ошибки на этапе извлечения данных, как правило, легко найти, и их также можно легко исправить.

Сбор данных: эти ошибки возникают во время сбора данных и их сложнее исправить. Их можно разделить на четыре типа:

Пропущено полностью случайно: это тот случай, когда вероятность пропуска переменной одинакова для всех наблюдений. Например: респонденты процесса сбора данных решают, что они объявят о своем заработке после того, как бросят монету. Если выпадает орел, респондент объявляет о своем заработке и наоборот. Здесь каждое наблюдение имеет равные шансы стать пропущенным значением.

Пропущено случайно: это случай, когда переменная отсутствует случайным образом, а коэффициент отсутствия изменяется для разных значений/уровня других входных переменных. Например: мы собираем данные по возрасту, и у женщин более высокая  доля отсутствующих данных по сравнению с мужчинами.

Пропуск зависит от ненаблюдаемых предикторов. Это тот случай, когда отсутствующие значения не случайны и связаны с ненаблюдаемой входной переменной. Например: если в медицинском исследовании определенная диагностика вызывает дискомфорт, то вероятность исключения ее из исследования выше. Это пропущенное значение не случайно, если мы не включили «дискомфорт» в качестве входной переменной для всех пациентов.

Отсутствие зависит от самого пропущенного значения: это тот случай, когда вероятность появления пропущенного значения напрямую связана с самим пропущенным значением. Например: люди с более высоким или низким доходом, скорее всего, не обнародуют свой заработок.

Какие имеются методы для обработки пропущенных значений?

Удаление: бывает двух типов: List Wise Deletion и Pair Wise Deletion.

- При "list wise deletion" мы удаляем наблюдения, в которых отсутствует любая переменная. Простота является одним из основных преимуществ этого метода, но этот метод уменьшает мощность модели, потому что он уменьшает размер выборки.

- В "pair wise deletion" мы проводим анализ всех случаев, в которых присутствуют представляющие интерес переменные. Преимущество этого метода заключается в том, что он сохраняет как можно больше случаев для анализа. Одним из недостатков этого метода является использование разного размера выборки для разных переменных.

Методы удаления используются, когда характер пропущенных данных «отсутствует полностью случайно», в противном случае неслучайные пропущенные значения могут повлиять на вывод модели.

Mean/ Mode/ Median Imputation: Imputation - это метод для заполнения пропущенных значений оценочными. Цель состоит в том, чтобы использовать известные отношения, которые могут быть идентифицированы в действительных значениях набора данных, чтобы помочь в оценке пропущенных значений. Mean/ Mode/ Median Imputation - один из наиболее часто используемых методов. Он состоит в замене отсутствующих данных для данного атрибута средним значением или медианой (количественный атрибут) или модой (качественный атрибут) всех известных значений этой переменной. Он может быть двух типов:

Generalized Imputation: в этом случае мы вычисляем среднее значение или медиану для всех не пропущенных значений этой переменной, а затем заменяем пропущенное значение средним или медианным. Как и в приведенной выше таблице, переменная «Manpower» отсутствует, поэтому мы берем среднее значение всех непропущенных значений «Manpower» (28,33) и затем заменяем на нее отсутствующее значение.

Similar case Imputation: в этом случае мы вычисляем среднее для пола «Male» (29,75) и «Female» (25) по отдельности, а затем заменяем пропущенное значение в зависимости от пола. Для «Male» мы заменим недостающие значения manpower на 29,75, а для «Female» - на 25.

Prediction Model. Является одним из сложных методов обработки отсутствующих данных. Здесь мы создаем прогнозирующую модель для оценки значений, которые заменят отсутствующие данные. В этом случае мы делим наш набор данных на два: один набор без пропущенных значений для переменной и другой набор с пропущенными значениями. Первый набор данных становится обучающим набором данных модели, в то время как второй набор данных с пропущенными значениями является тестовым набором, а переменная с пропущенными значениями рассматривается как целевая переменная. Затем мы создаем модель для прогнозирования целевой переменной на основе других атрибутов обучающего набора данных и заполняем пропущенные значения тестового набора. Для этого мы можем использовать регрессию, ANOVA, логистическую регрессию и различные методы моделирования. У этого подхода есть 2 недостатка:

Оценочные значения модели обычно ведут себя лучше, чем истинные значения.

Если в наборе данных нет связей атрибутов с отсутствующими значениями, то модель не будет точной для оценки отсутствующих значений.

KNN Imputation: В этом методе пропущенные значения атрибута определяются с использованием заданного количества атрибутов, которые наиболее похожи на атрибут, значения которого отсутствуют. Сходство двух атрибутов определяется с помощью функции расстояния. Также известно, что он имеет определенные преимущества и недостатки.

Преимущества:

Метод k-ближайших соседей может прогнозировать как качественные, так и количественные признаки.

Создание прогностической модели для каждого атрибута с отсутствующими данными не требуется.

Атрибуты с несколькими пропущенными значениями могут быть легко обработаны.

Учитывается корреляционная структура данных. 

Недостатки:

Алгоритм KNN очень трудоемкий при анализе большой базы данных. Он просматривает все наборы данных в поисках наиболее похожих экземпляров.

Выбор значения k очень важен. Более высокое значение k будет включать атрибуты, которые значительно отличаются от того, что нам нужно, в то время как более низкое значение k подразумевает отсутствие значимых атрибутов.

После работы с пропущенными значениями следующая задача - выбросы. Часто мы склонны пренебрегать выбросами при построении моделей. Это обескураживающая практика. Выбросы имеют тенденцию искажать ваши данные и снижают точность. Давайте узнаем больше о работе с ними.

3. Техника обнаружения и обработки выбросов

Что такое выброс?

Аналитики и исследователи данных часто используют термины «выбросы», так как они требуют пристального внимания, иначе это может привести к ошибочным оценкам. Проще говоря, выброс - это наблюдение, которое очень сильно отличается от общей модели в выборке.

Давайте рассмотрим пример, мы проводим профилирование клиентов и выясняем, что средний годовой доход клиентов составляет 0,8 миллиона долларов. Но есть два клиента с годовым доходом 4 и 4,2 миллиона долларов. У этих двух клиентов годовой доход намного выше, чем у остальных. Эти два наблюдения будут рассматриваться как выбросы.

Какие бывают типы выбросов?

Выброс может быть двух типов: одномерный и многомерный. Выше мы обсуждали пример одномерного выброса. Эти выбросы можно найти, когда мы смотрим на распределение одной переменной. Многомерные выбросы - это выбросы в n-мерном пространстве. Чтобы найти их, вы должны смотреть на распределения в нескольких измерениях.

Позвольте пояснить это на примере. Допустим, мы определяем связь между ростом и весом. Ниже мы имеем одномерное и двумерное распределение для роста, веса. Посмотрите на box plot. У нас нет никаких выбросов (выше и ниже 1,5*IQR, наиболее распространенный метод). Теперь посмотрим на график рассеяния. Здесь у нас есть два значения ниже и одно выше среднего в определенном сегменте веса и роста.

Что вызывает выбросы?

Всякий раз, когда мы сталкиваемся с выбросами, идеальный способ справиться с ними - выяснить причину наличия этих выбросов. Способ борьбы с ними будет зависеть от причины их возникновения. Причины выбросов можно классифицировать по двум широким категориям:

Искусственный (ошибка).

Естественный.

Давайте разберемся с различными типами выбросов более подробно:

Ошибки ввода данных: человеческие ошибки, такие как ошибки, при сборе, записи или вводе данных, могут привести к выбросам в данных. Например: годовой доход клиента составляет 100 000 долларов. Случайно оператор ввода данных ставит дополнительный ноль. Теперь доход становится 1 000 000 долларов, что в 10 раз выше. Очевидно, что это будет более значимое значение по сравнению с остальным населением выборки.

Ошибка измерения: это наиболее распространенный источник выбросов. Это происходит, когда используемый измерительный прибор оказывается неисправным. Например: есть 10 весов. 9 из них правильные, 1 неисправные. Вес, измеренный на неисправных весах, будет выше/ниже, чем у остальных людей в группе. Вес, измеренный на неисправных весах, может привести к выбросам.

Экспериментальная ошибка: другой причиной выбросов является экспериментальная ошибка. Например: в спринте на 100 м из 7 бегунов один из бегунов упустил возможность сконцентрироваться на страте, из-за чего он поздно стартовал. Следовательно, это привело к тому, что время бега было больше, чем у других бегунов. Его общее время может быть выбросом.

Преднамеренные выбросы: Это обычно встречается в самооценках, которые включают в себя конфиденциальные данные. Например: подростки обычно сообщают о количестве алкоголя, которое они потребляют. Только часть из них сообщит о реальном количестве. Здесь фактические значения могут выглядеть как выбросы, потому что остальные подростки занижают потребление.

Ошибка обработки данных: всякий раз, когда мы выполняем анализ данных, мы извлекаем данные из нескольких источников. Возможно, что некоторые манипуляции или ошибки извлечения могут привести к выбросам в наборе данных.

Ошибка выборки: например, мы должны измерить рост спортсменов. По ошибке мы включили в выборку несколько баскетболистов. Это включение может вызвать выбросы в наборе данных.

Естественный выброс: когда выброс не является искусственным (из-за ошибки), это естественный выброс. Например: во время работы в одной из известных страховых компаний я заметил, что эффективность 50 лучших финансовых консультантов была намного выше, чем у остальной части выборки. Удивительно, но это не было связано с какой-либо ошибкой. Следовательно, всякий раз, когда мы выполняем какие-либо действия по извлечению данных с консультантами, мы должны рассматривать этот сегмент отдельно.

Какое влияние оказывают выбросы на набор данных?

Выбросы могут кардинально изменить результаты анализа данных и статистического моделирования. Существует множество неблагоприятных воздействий выбросов в наборе данных:

Они увеличивают дисперсию ошибок и снижают мощность статистических тестов.

Если выбросы распределены не случайным образом, они могут снизить нормальность данных.

Они могут смещать или влиять на оценки, которые могут представлять существенный интерес

Они также могут влиять на базовое допущение регрессии, ANOVA и других допущений статистических моделей.

Чтобы глубже понять их влияние, давайте возьмем пример, чтобы проверить, что происходит с набором данных с выбросами в наборе данных и без них.

Пример:

Как видите, набор данных с выбросами имеет существенно различающиеся среднее значение и стандартное отклонение. В первом сценарии среднее значение составляет 5,45. Но с выбросом среднее взлетает до 30. Это полностью изменит оценку.

Как обнаружить выбросы?

Наиболее часто используемый метод обнаружения выбросов - визуализация. Мы используем различные методы визуализации, такие как Box-plot, Histogram, Scatter Plot (выше, мы использовали box-plot и scatter plot для визуализации). Некоторые аналитики также используют различные правила большого пальца, чтобы обнаружить выбросы. Некоторые из них:

Любое значение, выходящее за пределы диапазона от -1,5 x IQR до 1,5 x IQR.

Используйте методы укупорки. Любое значение, которое выходит за пределы 5-го и 95-го процентиля, может рассматриваться как выброс.

Точки данных, отстоящие на три или более стандартных отклонения от среднего значения считаются выбросами.

Обнаружение выбросов является лишь частным случаем проверки данных для влиятельных точек данных, а также зависит от понимания бизнеса.

Двумерные и многомерные выбросы обычно измеряются с использованием либо индекса влияния, либо рычага, либо расстояния. Популярные показатели, такие как расстояние Махаланобиса и Cook's D, часто используются для обнаружения выбросов.

В SAS мы можем использовать PROC Univariate, PROC SGPLOT. Чтобы выявить выбросы и влиятельные наблюдения, мы также рассматриваем статистические показатели, такие как STUDENT, COOKD, RSTUDENT и другие.

Как удалить выбросы?

Большинство способов борьбы с выбросами аналогичны методам работы с пропущенными значениями, таким как удаление наблюдений, их преобразование, объединение в группы, обработка их как отдельной группы, присвоение значений и другие статистические методы. Здесь мы обсудим общие методы, используемые для борьбы с выбросами:

Удаление наблюдений: мы удаляем значения выбросов, если они вызваны ошибкой ввода данных, ошибкой обработки данных или если выбросов очень мало. Мы также можем использовать обрезку на обоих концах для удаления выбросов.

Преобразование и объединение значений. Преобразование переменных также может устранить выбросы. Натуральный логарифм значения уменьшает отклонения, вызванные экстремальными значениями. Биннинг также является формой переменного преобразования. Алгоритм дерева решений (Decision Tree) позволяет хорошо справляться с выбросами за счет объединения переменных. Мы также можем использовать процесс присвоения весов различным наблюдениям.

Imputing: Как и в случае заполнения отсутствующих значений, мы также можем корректировать значения выбросов. Мы можем использовать методы применения среднего, и модального значений. Прежде чем переписывать значение, мы должны проанализировать, является ли это наблюдение естественным выбросом или искусственным. Если оно искусственное, мы можем переписать его значение. Мы также можем использовать статистическую модель для прогнозирования значений выбросов, и после этого мы можем присвоить им прогнозные значения.

Treat separately: если имеется значительное количество выбросов, мы должны рассматривать их отдельно в статистической модели. Один из подходов состоит в том, чтобы рассматривать обе группы как две разные группы и строить индивидуальную модель для обеих групп, а затем объединять результаты.

К этому моменту мы узнали об этапах исследования данных, обработке отсутствующих значений и методах обнаружения и обработки выбросов. Эти 3 этапа улучшат ваши необработанные данные с точки зрения доступности и точности информации. Теперь перейдем к финальной стадии исследования данных. Это конструирование признаков (Feature Engineering).

4. Искусство конструирования признаков

Что такое конструирование признаков?

Конструирование признаков - это наука (и искусство) получения дополнительной информации из существующих данных. Вы не добавляете сюда никаких новых данных, но фактически делаете данные, которые у вас уже есть, более полезными.

Например, предположим, что вы пытаетесь предсказать количество покупателей в торговом центре на основе дат. Если вы попытаетесь использовать даты напрямую, вы не сможете извлечь значимые данные из этих данных. Это связано с тем, что на количество покупателей меньше влияет день месяца, чем день недели. Сейчас эта информация о дне недели скрыта в ваших данных. Вы должны вытащить ее, чтобы сделать вашу модель лучше.

Это упражнение по извлечению информации из данных, известно как конструирование признаков.

В чем заключается процесс конструирования признаков?

Вы выполняете конструирование признаков после завершения первых 5 этапов исследования данных. Функциональность самого конструирования можно разделить на 2 этапа:

Преобразование переменных.

Создание переменных/объектов.

Эти два метода имеют жизненно важное значение для исследования данных и имеют замечательное влияние на эффективность прогнозирования. Давайте разберемся с каждым из этих шагов более подробно.

Что такое преобразование переменных?

В моделировании данных преобразование относится к замене переменной на функцию. Например, замена переменной x на квадратный/кубический корень или логарифм x является преобразованием. Другими словами, преобразование - это процесс, который изменяет распределение или отношения переменной с другими переменными.

Давайте посмотрим на ситуации, когда преобразование переменной полезно.

Когда мы должны использовать преобразование переменных?

Ниже приведены ситуации, когда преобразование переменных является обязательным условием:

Когда мы хотим изменить масштаб переменной или стандартизировать значения переменной для лучшего понимания. Хотя это преобразование является обязательным, если у вас есть данные в разных масштабах, это преобразование не меняет форму распределения переменных

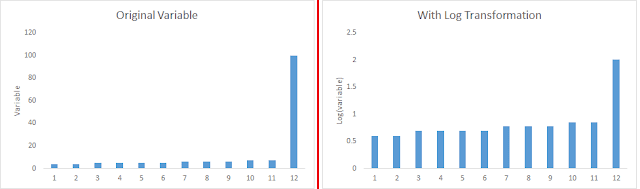
Когда мы можем преобразовать сложные нелинейные отношения в линейные. Наличие линейных отношений между переменными легче понять по сравнению с нелинейными отношениями. Преобразование помогает нам преобразовать нелинейное отношение в линейное. Точечный график может быть использован, чтобы найти связь между двумя непрерывными переменными. Эти преобразования также улучшают прогноз. Логарифмическое преобразование является одним из наиболее часто используемых методов преобразования, используемых в этих ситуациях.

Симметричное распределение предпочтительнее асимметричного распределения, поскольку его легче интерпретировать и генерировать выводы. Некоторые методы моделирования требуют нормального распределения переменных. Таким образом, всякий раз, когда у нас есть асимметричное распределение, мы можем использовать преобразования, которые уменьшают асимметрию. Для распределения с правым наклоном мы берем квадратный/кубический корень или логарифм переменной, а для распределения с левым наклоном - квадрат/куб или экспоненту.

Преобразование переменных также выполняется с точки зрения реализации (участие человека). Давайте разберемся с этим более понятными словми. В одном из моих проектов, касающихся эффективности работы сотрудников, я обнаружил, что возраст напрямую связан с результатами работы сотрудника, т. е. чем выше возраст, тем выше производительность. С точки зрения реализации, запуск программы на базе возраста может представлять проблему для реализации. Тем не менее, классификация агентов по продажам по трем возрастным группам <30 30-45="">45, а затем формулировка трех различных стратегий для каждой группы является разумным подходом. Этот метод классификации известен как биннинг переменных.

Каковы наиболее распространенные методы преобразования переменных?

Существуют различные методы, используемые для преобразования переменных. Как уже говорилось, некоторые из них включают в себя квадратный корень, кубический корень, логарифмы, биннинг и многие другие. Давайте рассмотрим эти методы более подробно, выделив преимущества и недостатки этих методов преобразования.

Логарифмирование переменной - это распространенный метод преобразования, используемый для изменения формы распределения переменной на графике распределения. Обычно используется для уменьшения правой асимметрии переменных. Тем не менее, он не может быть применен к нулевым или отрицательным значениям.

Квадратный/кубический корень: квадратный и кубический корень переменной оказывает значительный эффект на распределение переменной, однако это не такой сильный, как логарифмическое преобразование. Кубический корень имеет преимущество, так как может применяться к отрицательным значениям, включая ноль. Квадратный корень может быть применен только к положительным значениям, включая ноль.

Биннинг: используется для классификации переменных. Выполняется по исходным значениям, процентилям или частоте. Решение о технике категоризации основано на понимании данных. Например, мы можем классифицировать доход по трем категориям, а именно: Высокий, Средний и Низкий. Мы также можем выполнять ковариационный биннинг, который зависит от значения более чем одной переменной.

Что такое создание признаков/переменных и какие у него преимущества?

Создание признака/переменной - это процесс создания новых переменных/признаков на основе существующих переменных. Например, скажем, у нас есть дата (дд-мм-гг) в качестве входной переменной в наборе данных. Мы можем генерировать новые переменные, такие как день, месяц, год, неделя, день недели, которые могут лучше соотноситься с целевой переменной. Этот шаг используется для выделения скрытых отношений в переменной:

Существуют различные методы для создания новых признаков. Давайте посмотрим на некоторые из наиболее часто используемых методов:

Создание производных переменных: это относится к созданию новых переменных из существующих переменных с использованием набора функций или различных методов. Давайте посмотрим на это через «Titanic – Kaggle competition». В этом наборе данных переменная age имеет пропущенные значения. Чтобы предсказать пропущенные значения, мы использовали обращение (Master, Mr, Miss, Mrs) в качестве новой переменной. Как мы решаем, какую переменную создать? Честно говоря, это зависит от понимания аналитика, его любопытства и гипотезы о проблеме, которая у него может быть. Такие методы, как получение логарифма переменных, биннинга и другие методы преобразования переменных, также могут использоваться для создания новых переменных.

Создание фиктивных переменных. Одним из наиболее распространенных применений фиктивных переменных является преобразование категориальной переменной в числовые переменные. Фиктивные переменные также называются Indicator Variables. В качестве предиктора в статистических моделях полезно принять категориальную переменную. Категориальная переменная может принимать значения 0 и 1. Давайте возьмем переменную «пол». Мы можем создать две переменные, а именно: «Var_Male» со значениями 1 (мужчина) и 0 (не мужчина) и «Var_Female» со значениями 1 (женщина) и 0 (не женщина). Мы также можем создать фиктивные переменные для более чем двух классов категориальных переменных с n или n-1 фиктивными переменными.

Заключение

Как упоминалось в начале, усилия, вложенные в исследование данных, отличают хорошую модель от плохой.

На этом наше руководство по исследованию и подготовке данных заканчивается. В этом всеобъемлющем руководстве мы подробно рассмотрели семь этапов исследования данных. Целью этой статьи было предоставить подробное и пошаговое руководство по чрезвычайно важному процессу в науке о данных.