Перевод. Оригинал: Statistics for Data Science: Introduction to t-test and its Different Types (with Implementation in R)
Введение
Каждый день мы испытываем новые идеи, находим самый быстрый путь к офису, самый быстрый способ закончить нашу работу или просто ищем лучший способ сделать то, что мы любим. Таким образом, главный вопрос заключается в том, является ли наша идея значительно лучше, чем то, что мы пробовали ранее.
Эти идеи, которые мы выдвигаем на такой регулярной основе, - это, по сути, гипотеза. И проверка этих идей, чтобы выяснить, какая из них работает, а какую лучше оставить позади, называется проверкой гипотез.
Проверка гипотез - одна из самых захватывающих вещей, которые мы делаем как ученые с данными. На данном этапе нашего проекта ни одна идея не запрещена. Я лично видел так много идей, получаемых при проверке гипотез - идеи, которые большинство из нас пропустили бы, если бы не этот этап!
Одним из наиболее популярных способов проверки гипотез является концепция, называемая t-тест. Как мы скоро увидим, существуют разные типы t-тестов, и у каждого есть свое уникальное приложение. Если вы начинающий специалист по данным, вы должны знать, что такое t-тест и когда вы можете его использовать.
Итак, в этой статье мы узнаем о различных ньюансах t-теста, а затем рассмотрим три различных типа t-теста. Вишенка на торте? Мы реализуем каждый тип t-теста в R, чтобы визуализировать, как они работают в практических сценариях.
Примечание. Вам следует ознакомиться с приведенной ниже статьей, если вам необходимо освежить свои концепции проверки гипотез:
Когда мы должны выполнять t-тест?
Давайте сначала разберемся, где можно использовать t-тест, прежде чем мы углубимся в его различные типы и их реализации. Я твердо верю, что лучший способ выучить концепцию - это представить ее на примере. Итак, давайте возьмем простой пример, чтобы увидеть, где пригодится t-критерий.
Рассмотрим телекоммуникационную компанию, которая имеет в городе два сервисных центра. Компания хочет выяснить, является ли среднее время, необходимое для обслуживания покупателя, одинаковым в обоих магазинах.
Компания измеряет среднее время, затрачиваемое 50 случайными покупателями в каждом магазине. Время для магазина A составляет 22 минуты, а для магазина B - в среднем 25 минут. Можно ли сказать, что магазин A более эффективен, чем Магазин B, с точки зрения обслуживания клиентов?
Это очевидно, не так ли? Тем не менее, мы рассмотрели только 50 случайных покупателей из множества людей, которые посещают магазины. Простой взгляд на среднее время выборки может не отражать всех клиентов, посещающих оба магазина.
Здесь в игру вступает t-тест. Он поможет нам понять, является ли разница между двумя выборками на самом деле реальной или просто случайной.
Допущения для выполнения t-теста
Есть определенные допущения, которые мы должны сделать перед выполнением t-теста:
1. Данные должны быть непрерывными или порядковыми (например, по результатам тестов IQ студентов).
2. Наблюдения в данных должны выбираться случайным образом.
3. Данные должны напоминать колоколообразную кривую при построении графика, то есть они должны быть нормально распределены. Вы можете обратиться к этой статье, чтобы лучше понять нормальное распределение.
3. Достаточно большой объем выборки должен быть взят для того, чтобы данные приблизились к нормальному распределению (хотя t-критерий важен для небольших выборок, так как их распределение не нормальное)
4. Дисперсии выборок должны быть одинаковыми (для независимого t-критерия с двумя выборками)
Итак, каковы различные типы t-тестов? Когда мы должны выполнять каждый тип? Мы ответим на эти вопросы в следующем разделе и посмотрим, как мы можем выполнить каждый тип t-теста в R.
Типы t-тестов (с решенными примерами в R)
Существует три типа t-тестов, которые мы можем выполнить на основе имеющихся данных:
Одновыборочный t-тест
Двухвыборочный t-критерий для независимых выборок
Двухвыборочный t-критерий для зависимых выборок
В этом разделе мы рассмотрим каждый из этих типов более подробно. Я также предоставил код R для каждого типа t-теста, чтобы вы могли выполнять их реализации. Это отличный способ узнать и понять, насколько полезны эти t-тесты!
Одновыборочный t-тест
В одновыборочном t-тесте мы сравниваем среднее одной группы с заданным средним. Это заданное среднее значение может быть любым теоретическим значением (или средним для выборки).
Рассмотрим следующий пример. Исследователь хочет определить, отличается ли среднее время съедания бургера (стандартного размера) от заданного значения. Допустим, это значение составляет 10 минут. Как вы думаете, может ученый определить это?
Он/она может широко выполнить следующие шаги:
1. Выбрать группу людей.
2. Записать время съедания бургера стандартного размера для каждого участника группы.
3. Рассчитать среднее время еды для группы.
4. Наконец, сравнить это среднее значение с установленным значением 10.
Вкратце, именно так мы можем выполнить одновыборочный t-тест. Вот формула для его расчета:
где,
t = t-статистика
m = среднее по группе
µ = теоретическое значение или генеральная средняя
s = стандартное отклонение группы
n = размер группы или размер выборки
Примечание. Как упоминалось ранее в допущениях, для получения данных, приближающихся к нормальному распределению, следует брать большой объем выборки (Хотя t-критерий необходим для небольших выборок, поскольку их распределение ненормальное).
Как только мы вычислим значение t-статистики, следующая задача - сравнить его с критическим значением t-критерия. Мы можем найти его в приведенной ниже таблице t-критерия в зависимости от степени свободы (n-1) и уровня значимости:
Этот метод помогает нам проверить, является ли разница между средними значениями статистически значимой или нет. Давайте еще больше укрепим наше понимание одновыборочного t-теста, выполнив его в R.
Реализация одновыборочного t-теста в R
Компания-производитель мобильных телефонов взяла образец мобильных телефонов той же модели по данным предыдущего месяца. Они хотят проверить, отличается ли средний размер экрана образца от желаемой длины в 10 см. Вы можете скачать данные здесь.
Шаг 1. Сначала импортируйте данные.
Шаг 2: Подтвердите их корректность в R:
#Импорт данных
#_______________________________________________________
#Импорт данных csv
data<-read.csv(file.choose())
#Проверка корректности данных
#______________________________________________________
#Количество строк и столбцов
dim(data)
#Выводим первые 10 строк набора данных
head(data,10)
Вывод:
#Количество строк и столбцов
[1] 1000 1
> #Выводим первые 10 строк набора данных
Screen_size.in.cm.
1 10.006692
2 10.081624
3 10.072873
4 9.954496
5 9.994093
6 9.952208
7 9.947936
8 9.988184
9 9.993365
10 10.016660
Шаг 3: Помните предположения, которые мы обсуждали ранее? Нам нужно проверить их:
#Проверка предположений
#______________________________________________________
#1. Данные непрерывны
#2. Наблюдения выбраны случайно
#3. Для проверки нормальности распределения данных используем следующий код:
qqnorm(data$Screen_size.in.cm.)
qqline(data$Screen_size.in.cm.,col="red")
Мы получаем приведенный ниже график Q-Q:
Почти все значения лежат на красной линии. Мы можем с уверенностью сказать, что данные следуют нормальному распределению.
Шаг 4: Выполните одновыборочный t-тест:
#Одновыборочный t-test
#Нулевая гипотеза: Средний размер экрана не отличается от 10 см
#Альтернативная гипотеза: средний размер экрана отличается от 10 см.
t.test(data$Screen_size.in.cm.,mu=10)
Вывод:
One Sample t-test
data: data$Screen_size.in.cm.
t = -0.39548, df = 999, p-value = 0.6926
alternative hypothesis: true mean is not equal to 10
95 percent confidence interval:
9.996361 10.002418
sample estimates:
mean of x
9.99939
t-статистика имеет значение -0,39548. Обратите внимание, что мы можем рассматривать здесь отрицательные значения как их положительный аналог. Теперь обратитесь к таблице, упомянутой ранее, для поиска критического значения t. Степень свободы здесь составляет 999, а доверительный интервал составляет 95%.
Критическое значение t составляет 1,962. Поскольку t-статистика меньше, чем критическое значение t, мы не можем отклонить нулевую гипотезу и можем сделать вывод, что средний размер экрана образца не отличается от 10 см.
Мы также можем проверить это по значению р, которое больше 0,05. Поэтому мы не можем отклонить нулевую гипотезу с 95% доверительным интервалом.
Двухвыборочный t-критерий для независимых выборок
Двухвыборочный t-критерий используется для сравнения средних значений двух разных выборок.
Допустим, мы хотим сравнить средний рост работников - мужчин со средним ростом женщин. Конечно, количество мужчин и женщин должно быть равным для этого сравнения. Здесь используется двухвыборочный t-критерий.
Вот формула для вычисления t-статистики для двухвыборочного t-теста:
где,
mA и mB - это две разные выборки.
nA и nB - размеры выборок.
S2 является оценкой общей дисперсии двух выборок, такой как:
Здесь степень свободы равна nA + nB - 2.
Мы будем следовать той же логике, которую мы видели в одновыборочном t-тесте, чтобы проверить, значительно ли среднее значение для одной группы отличается от другой группы. Мы сравним вычисленную t-статистику с критическим значением t.
Давайте возьмем пример двухвыборочного t-теста для независимых выборок и решим его в R.
Реализация двухвыборочного t-теста для независимых выборок в R
В этом разделе мы будем работать с данными о двух образцах различных моделей мобильного телефона. Мы хотим проверить, отличается ли средний размер экрана выборки 1 от среднего размера экрана выборки 2. Данные можно скачать здесь.
Шаг 1: Опять же, сначала импортируйте данные.
Шаг 2: Проверьте их на правильность в R:
#Импорт данных
#_______________________________________________________
#импортируем данные csv
data<-read.csv(file.choose())
#Проверка корректности данных
#______________________________________________________
#считаем количество строк и столбцов
dim(data)
#выводим первые 10 строк набора данных
head(data,10)
Шаг 3: Нам нужно проверить предположения, как мы делали выше. Я оставлю это упражнение на ваше усмотрение.
Также в этом случае мы проверим однородность дисперсии:
#однородность дисперсии
var(data$screensize_sample1)
var(data$screensize_sample2)
Вывод:
#однородность дисперсии
> var(data$screensize_sample1)
[1] 0.00238283
> var(data$screensize_sample2)
[1] 0.002353585
Отлично, дисперсии равны. Мы можем двигаться вперед.
Шаг 4: Проведите двухвыборочный t-тест для независимых выборок:
#двухвыборочный t-тест
# Нулевая гипотеза: нет разницы между средним двух выборок
# Альтернативная гипотеза: между средними двух выборок есть разница
t.test(data$screensize_sample1,data$screensize_sample2,var.equal = T)
Примечание. Перепишите приведенный выше код с «var.equal = F», если вы получили неравные или неизвестные дисперсии. Это будет случай t-теста Уэлча, который используется для сравнения средних значений двух выборок с неравными дисперсиями.
Вывод:
Two Sample t-test
data: data$screensize_sample1 and data$screensize_sample2
t = 1.3072, df = 1998, p-value = 0.1913
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.001423145 0.007113085
sample estimates:
mean of x mean of y
10.000976 9.998131
Что вы можете определить из вышеприведенного вывода? Мы можем подтвердить, что t-статистика снова меньше критического значения, поэтому мы не можем отвергнуть нулевую гипотезу. Следовательно, мы можем сделать вывод, что нет разницы между средним значением обеих выборок.
Мы можем проверить это снова, используя p-значение. Получается, что оно больше 0,05, поэтому мы не можем отклонить нулевую гипотезу с 95% доверительным интервалом. Нет разницы между средним двух образцов.
Двухвыборочный t-тест для зависимых выборок
Двухвыборочный t-тест для зависимых выборок довольно интригующий. Здесь мы изучаем одну группу в два разных промежутка времени. Мы сравниваем отдельные средние для группы в два разных отрезка времени или в двух разных условиях. Смущены? Позволь мне объяснить.
Некий менеджер понял, что уровень производительности его сотрудников значительно снизился. Этот менеджер решил провести программу обучения для всех своих сотрудников с целью повышения их производительности.
Как менеджер будет измерять увеличение уровня производительности? Это просто - просто сравните уровень производительности сотрудников до и после программы обучения.
Здесь мы сравниваем одну и ту же выборку (сотрудников) за два разных отрезка времени (до и после обучения). Здесь пример t-теста для зависимых выборок. Формула для расчета t-статистики для двухвыборочного t-теста для зависимых выборок:
где,
t = t-статистика
m = среднее по группе
µ = теоретическое значение или среднее значение по генеральной совокупности
s = стандартное отклонение группы
n = размер группы или размер выборки
Мы можем принять степень свободы в этом тесте как n - 1, так как участвует только одна группа. Теперь давайте решим пример в R.
Реализация двухвыборочного t-теста для зависимых выборок в R
Менеджер компании по производству шин хочет сравнить резину для двух партий шин. Один из способов сделать это - проверить разницу между средним расстоянием, пройденным одной парой шин до износа.
Вы можете скачать данные здесь. Давай сделаем это!
Шаг 1. Сначала импортируйте данные.
Шаг 2: Проверьте их на правильность в R:
#Импорт данных
#_______________________________________________________
#импортируем данные csv
data<-read.csv(file.choose())
#Проверка корректности данных
#______________________________________________________
#считаем количество строк и столбцов
dim(data)
#выводим первые 10 строк набора данных
head(data,10)
Шаг 3: Теперь мы проверяем допущения так же, как мы делали в одновыборочном t-тесте. Я снова оставлю это тебе.
Шаг 4: Проведите двухвыборочный t-тест для зависимых выборок:
#Двухвыборочный t-тест для зависимых выборок
# Нулевая гипотеза: нет разницы между средним расстоянием для шин до и после замены резины.
# Альтернативная гипотеза: Существует разница между средним расстоянием для шин до и после замены резины.
t.test(data$tyre_1,data$tyre_2,paired = T)
Вывод:
Paired t-test
data: data$tyre_1 and data$tyre_2
t = -5.2662, df = 24, p-value = 2.121e-05
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2201.6929 -961.8515
sample estimates:
mean of the differences
-1581.772
Вы должны быть профессионалом в расшифровке этого вывода! Значение р составляет менее 0,05. Мы можем отклонить нулевую гипотезу с 95-процентным доверительным интервалом и сделать вывод, что существует значительная разница между средними показателями шин до и после замены резины.
Отрицательное среднее в разнице показывает, что среднее расстояние, пройденное шиной 2, больше, чем среднее расстояние, пройденное шиной 1.
Заключение
В этой статье мы узнали о концепции t-теста, необходимых допущениях, а также о трех различных типах t-тестов с их реализациями в R. t-критерий имеет как статистическую значимость, так и практические применения в реальном мире.







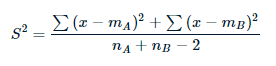


Комментариев нет:
Отправить комментарий