Перевод. Оригинал: Neural Network In Python: Introduction, Structure And Trading Strategies
Исследования нейронных сетей были начаты с целью симулировать человеческий мозг и понять, как люди принимают решения. Иногда нам не удается осознать, что человеческий мозг, возможно, является наиболее сложной машиной в этом мире и, как известно, весьма эффективно делает выводы в рекордно короткие сроки.
Подумайте об этом: если бы мы могли использовать то, как работает наш мозг, и применить его в области машинного обучения (в конце концов, нейронные сети являются подмножеством машинного обучения), мы могли бы сделать гигантский скачок с точки зрения вычислительной мощности и вычислительных ресурсов.
Прежде чем мы углубимся в мелочи торговли с нейронными сетями, мы должны понять работу основного компонента, то есть нейрона.
Помните, конечная цель руководства по нейронным сетям состоит в том, чтобы понять концепции, связанные с нейронными сетями, и то, как их можно применять для прогнозирования цен на акции на реальных рынках. Давайте начнем с понимания, что такое нейрон.
Структура нейрона
Нейрон состоит из трех компонентов: дендритов, аксонов и основной части нейрона. Дендриты - это приемники сигнала, а аксон - это передатчик. В одиночку нейрон не очень полезен, но когда он подключен к другим нейронам, он выполняет несколько сложных вычислений и помогает управлять самой сложной машиной на нашей планете, человеческим телом.
Персептрон: компьютерный нейрон
Персептрон, т. е. компьютерный нейрон, построен аналогичным образом, как показано на схеме.
Есть входы в нейрон, отмеченные желтыми кружками, и нейрон испускает выходной сигнал после некоторого вычисления.
Входной слой напоминает дендриты нейрона, а выходной сигнал - аксон. Каждому входному сигналу присваивается вес, wi. Этот вес умножается на входное значение, и нейрон сохраняет взвешенную сумму всех входных переменных. Эти весовые коэффициенты вычисляются на этапе обучения нейронной сети с помощью понятий, называемых градиентным спуском и обратным распространением, о которых мы расскажем позже.
Затем к взвешенной сумме применяется функция активации, что дает выходной сигнал нейрона.
Входные сигналы генерируются другими нейронами, то есть выходом других нейронов, и сеть строится таким образом, чтобы делать предсказания/вычисления.
Это основная идея нейронной сети. Мы рассмотрим каждую из этих концепций более подробно далее.
Понимание нейронной сети
Мы рассмотрим пример, чтобы понять работу нейронных сетей. Входной слой состоит из параметров, которые помогут нам получить выходное значение или сделать прогноз. Наш мозг по существу имеет пять основных входных параметров, которые являются нашими чувствами.
Нейроны в нашем мозге создают более сложные параметры, такие как эмоции и чувства, из этих основных входных параметров. И наши эмоции и чувства заставляют нас действовать или принимать решения, которые в основном являются результатом работы нейронной сети нашего мозга. Следовательно, в этом случае перед принятием решения существует два уровня вычислений.
Первый уровень принимает пять чувств в качестве входных данных и приводит к эмоциям и чувствам, которые являются входными данными для следующего уровня вычислений, где выходными данными являются решение или действие.
Следовательно, в этой чрезвычайно упрощенной модели работы человеческого мозга мы имеем один входной слой, два скрытых слоя и один выходной слой. Конечно, из нашего опыта мы все знаем, что мозг намного сложнее, чем этот пример, но по сути это то, как выполняются вычисления в нашем мозге.
Нейронная сеть в трейдинге: пример
Чтобы понять работу нейронной сети в торговле, давайте рассмотрим простой пример прогнозирования цены акций, где значения OHLCV (Open-High-Low-Close-Volume) являются входными параметрами, имеется один скрытый слой и выход состоит из прогноза цены акций.
В примере, взятом из учебника по нейронной сети, есть пять входных параметров, как показано на диаграмме.
Скрытый слой состоит из 3 нейронов, и результатом в выходном слое является прогноз для цены акций.
3 нейрона в скрытом слое будут иметь разные веса для каждого из пяти входных параметров и могут иметь разные функции активации, которые будут активировать входные параметры в соответствии с различными комбинациями входов.
Например, первый нейрон может смотреть на объем и разницу между ценой закрытия и открытия и может игнорировать цены максимума и минимума. В этом случае веса для цен High и Low будут равны нулю.
Основываясь на весах, которые модель вычисляет в ходе обучения, к взвешенной сумме в нейроне будет применена функция активации, что даст выходное значение для этого конкретного нейрона.
Точно так же два других нейрона приведут к выходному значению на основе их индивидуальных функций активации и весов. Наконец, выходное значение или прогнозируемое значение цены акций будет суммой трех выходных значений каждого нейрона. Так будет работать нейронная сеть для прогнозирования цен на акции.
Теперь, когда вы понимаете работу нейронной сети, мы переходим к сути, и рассмотрим, как искусственная нейронная сеть будет обучаться для прогнозирования движения цены акций.
Обучение нейронной сети
Чтобы упростить задачу, можно сказать, что существует два способа написания программы для выполнения конкретной задачи.
Определите все правила, требуемые программой для вычисления результата с учетом некоторого ввода данных в программу.
Разработайте структуру, на которой код научится выполнять определенную задачу, обучая себя на наборе данных, корректируя вычисляемый результат так, чтобы он был максимально приближен к фактическим результатам.
Второй процесс называется обучением модели, на котором мы сосредоточимся. Давайте посмотрим, как наша нейронная сеть будет обучаться прогнозировать цены на акции.
Нейронной сети будет предоставлен набор данных, который состоит из данных OHLCV в качестве входных, а также выходных данных. Мы также дадим модели цену закрытия следующего дня, это значение, наша модель должна научиться предсказывать. Фактическое значение выходных данных будет представлено как «y», а прогнозируемое значение будет представлено как y^, y hat.
Обучение модели включает в себя корректировку весов переменных для всех различных нейронов, присутствующих в нейронной сети. Это делается путем минимизации «функции стоимости». Функция стоимости, как следует из названия, - это стоимость прогнозирования с использованием нейронной сети. Это мера того, насколько далеко прогнозируемое значение, y ^, от фактического или наблюдаемого значения, y.
Есть много функций стоимости, которые используются на практике, самая популярная из них вычисляется как половина суммы квадратов разностей между фактическими и прогнозируемыми значениями для обучающего набора данных.
Обучение нейронной сети заключается в том, чтобы сначала вычислить функцию стоимости для обучающего набора данных для заданного набора весов для нейронов. Затем веса корректируются, а затем вычисляет функцию стоимости для обучающего набора данных на основе новых весов. Процесс отправки ошибок обратно в сеть для корректировки весов называется обратным распространением ошибки.
Это повторяется несколько раз, пока функция стоимости не будет минимизирована. Далее мы рассмотрим, как корректируются веса и как минимизируется функция стоимости.
Веса корректируются для минимизации функции стоимости. Один из способов сделать это - грубая сила. Предположим, мы берем 1000 значений для весов и оцениваем функцию стоимости для этих значений. Когда мы построим график функции стоимости, как показано ниже.
Наилучшим значением для весов будет функция стоимости, соответствующая минимумам этого графика.
Этот подход может быть успешным для нейронной сети с одним весом, который необходимо оптимизировать. Однако по мере того, как количество весов, подлежащих настройке, и количество скрытых слоев увеличивается, количество необходимых вычислений резко возрастет.
Время, необходимое для обучения такой модели, будет чрезвычайно большим даже на самом быстром в мире суперкомпьютере. По этой причине важно разработать лучшую, более быструю методологию для вычисления весов нейронной сети. Этот процесс называется градиентным спуском (Gradient Descent). Мы рассмотрим эту концепцию в следующей части.
Градиентный спуск (Gradient Descent)
Градиентный спуск включает в себя анализ наклона кривой функции стоимости. Основываясь на наклоне, мы корректируем веса, чтобы минимизировать функцию стоимости поэтапно, а не вычислять значения для всех возможных комбинаций.
Визуализация градиентного спуска показана на диаграммах ниже. Первый график представляет собой одно значение весов и, следовательно, является двухмерным. Можно видеть, что красный шар движется зигзагообразно, чтобы достичь минимума функции стоимости.
На второй диаграмме мы должны отрегулировать два веса, чтобы минимизировать функцию стоимости. Поэтому мы можем визуализировать ее как контур, как показано на графике, где мы движемся в направлении самого крутого склона, чтобы достичь минимумов в кратчайшие сроки. При таком подходе нам не нужно делать много вычислений, и в результате вычисления не занимают много времени, что делает обучение модели выполнимой задачей.
Градиентный спуск может быть выполнен тремя возможными способами,
- пакетный градиентный спуск (batch gradient descent);
- стохастический градиентный спуск (stochastic gradient descent);
- мини-градиентный спуск (mini-batch gradient descent).
При пакетном градиентном спуске функция стоимости вычисляется путем суммирования всех отдельных функций стоимости в наборе обучающих данных, а затем вычисления наклона и корректировки весов.
При стохастическом градиентном спуске наклон функции стоимости и корректировки весов выполняются после каждого ввода данных в набор данных обучения. Это чрезвычайно полезно, чтобы не застрять на локальных минимумах, если кривая функции стоимости не является строго выпуклой. Каждый раз, когда вы запускаете стохастический градиентный спуск, процесс достижения глобальных минимумов будет отличаться. Пакетный градиентный спуск может привести к зависанию с не оптимальным результатом, если он остановится на локальных минимумах.
Третий тип - это мини-градиентный спуск, который представляет собой комбинацию пакетного и стохастического методов. Здесь мы создаем разные пакеты, объединяя несколько записей данных в одном пакете. По сути, это приводит к реализации стохастического градиентного спуска для больших пакетов записей данных в наборе обучающих данных.
Хотя мы можем глубоко погрузиться в градиентный спуск, мы боимся, что это выйдет за рамки нашей статьи. Поэтому давайте продолжим и поймем, как работает обратное распространение для корректировки весов в соответствии со сгенерированной ошибкой.
Обратное распространение
Обратное распространение - это продвинутый алгоритм, который позволяет нам обновлять все веса в нейронной сети одновременно. Это значительно снижает сложность процесса регулировки весов. Если бы мы не использовали этот алгоритм, нам пришлось бы корректировать каждый вес в отдельности, выясняя, какое влияние этот конкретный вес оказывает на ошибку в прогнозе. Давайте посмотрим на этапы обучения нейронной сети с помощью Stochastic Gradient Descent:
1. Инициализация весов небольшими числами, очень близкими к 0 (но не к 0).
2. Прямое распространение - нейроны активируются слева направо, используя первую запись данных в нашем обучающем наборе данных, пока мы не достигнем предсказанного результата y.
3. Измеряется полученная ошибка.
4. Обратное распространение - полученная ошибка будет распространяться справа налево, а весовые коэффициенты будут корректироваться в зависимости от скорости обучения.
5. Повторение предыдущих трех шагов: прямое распространение, вычисление ошибок и обратное распространение для всего обучающего набора данных.
6. Это будет означать конец первого этапа, последующие этапы начнутся со значений веса предыдущих этапов, мы можем остановить этот процесс, когда функция стоимости сходится в пределах определенного приемлемого предела.
Теперь пора применять рассмотренные концепции на практике. Сейчас мы узнаем, как разработать собственную искусственную нейронную сеть для прогнозирования движения цены акций.
Вы поймете, как кодировать стратегию, используя прогнозы из нейронной сети, которую мы будем строить с нуля. Вы также узнаете, как кодировать искусственную нейронную сеть на Python, используя мощные библиотеки для построения надежной торговой модели с использованием возможностей нейронных сетей.
Кодирование стратегии
Импорт библиотек
Мы начнем с импорта нескольких библиотек, остальные будут импортированы по мере использования в программе на разных этапах. Сейчас мы импортируем библиотеки, которые помогут нам в импорте и подготовке набора данных для обучения и тестирования модели.
import numpy as np import pandas as pd import talib
Numpy - это фундаментальный пакет для научных вычислений, мы будем использовать эту библиотеку для вычислений в нашем наборе данных. Библиотека импортируется с использованием псевдонима np.
Pandas поможет нам в использовании мощного объекта dataframe, который будет использоваться в коде для построения искусственной нейронной сети в Python.
Talib - это библиотека технического анализа, которая будет использоваться для вычисления RSI и Williams% R. Они будут использоваться как функции для обучения нашей искусственной нейронной сети. Мы могли бы добавить гораздо больше признаков, используя эту библиотеку.
Установка фиксированного числа для random.seed
import random random.seed(42)
Random будет использоваться для инициализации фиксированного начального числа, чтобы при каждом запуске кода мы начинали с одними и теми же числами.
Импорт набора данных
dataset = pd.read_csv('RELIANCE.NS.csv')
dataset = dataset.dropna()
dataset = dataset[['Open', 'High', 'Low', 'Close']]
Затем мы импортируем наш набор данных, который хранится в файле .csv с именем «RELIANCE.NS.csv». Это делается с помощью библиотеки pandas, и данные хранятся в dataframe с именем dataset. Затем мы удаляем отсутствующие значения в наборе данных с помощью функции dropna(). Файл csv содержит ежедневные данные OHLC для акций Reliance, торгуемых на NSE, за период с 1 января 1996 года по 15 января 2018 года.
Мы выбираем только данные OHLC из этого набора данных, который также будет содержать данные о дате, скорректированной цене закрытии и объеме. Мы будем строить наши входные функции, используя только значения OHLC.
Подготовка набора данных
dataset['H-L'] = dataset['High'] - dataset['Low']
dataset['O-C'] = dataset['Close'] - dataset['Open']
dataset['3day MA'] = dataset['Close'].shift(1).rolling(window = 3).mean()
dataset['10day MA'] = dataset['Close'].shift(1).rolling(window = 10).mean()
dataset['30day MA'] = dataset['Close'].shift(1).rolling(window = 30).mean()
dataset['Std_dev']= dataset['Close'].rolling(5).std()
dataset['RSI'] = talib.RSI(dataset['Close'].values, timeperiod = 9)
dataset['Williams %R'] = talib.WILLR(dataset['High'].values, dataset['Low'].values, dataset['Close'].values, 7)
Затем мы подготавливаем различные входные функции, которые будут использоваться искусственными нейронными сетями для составления прогнозов. Мы определяем следующие функции ввода:
High минус Low
Close минус Open
Трехдневная скользящая средняя
Скользящее среднее за десять дней
Скользящее среднее за 30 дней
Стандартное отклонение за 5 дней
Индекс относительной силы RSI
Williams %R
dataset['Price_Rise'] = np.where(dataset['Close'].shift(-1) > dataset['Close'], 1, 0)
Затем мы определяем выходное значение как рост цены, который представляет собой двоичную переменную, хранящую 1, когда цена закрытия завтра больше, чем цена закрытия сегодня.
dataset = dataset.dropna()
Затем мы удаляем все строки, хранящие значения NaN, используя функцию dropna().
X = dataset.iloc[:, 4:-1] y = dataset.iloc[:, -1]
Затем мы создаем два фрейма данных, в которых хранятся входные и выходные переменные. dataframe «X» хранит входные объекты, столбцы, начиная с пятого столбца (или индекса 4) набора данных и заканчивая вторым последним столбцом. Последний столбец будет сохранен в dataframe y, который представляет собой значение, которое мы хотим предсказать, т.е. рост цены.
Разделение набора данных
split = int(len(dataset)*0.8)
X_train, X_test, y_train, y_test = X[:split], X[split:], y[:split], y[split:]
В этой части кода мы разделим наши входные и выходные переменные, чтобы создать наборы данных test и train. Это делается путем создания переменной с именем split, которая определяется как целочисленное значение, составляющее 0,8 от длины набора данных.
Затем мы разрезаем переменные X и Y на четыре отдельных dataframe: Xtrain, Xtest, ytrain и ytest. Это неотъемлемая часть любого алгоритма машинного обучения, обучающие данные используются моделью для определения весов модели. Тестовый набор данных используется, чтобы проверить, как модель будет работать с новыми данными, которые будут введены в модель. Тестовый набор данных также имеет фактическое значение для вывода, он помогает нам понять, насколько эффективна модель. Далее мы рассмотрим матрицу ошибок, которая, по сути, является мерой того, насколько точны прогнозы, сделанные моделью.
Масштабирование признаков
from sklearn.preprocessing import StandardScaler sc = StandardScaler() X_train = sc.fit_transform(X_train) X_test = sc.transform(X_test)
Другим важным шагом в предварительной обработке данных является стандартизация набора данных. Этот процесс делает среднее значение всех входных объектов равным нулю, а также преобразует их дисперсию в 1. Это гарантирует, что при обучении модели не будет смещения из-за разных масштабов всех входных объектов. Если этого не сделать, нейронная сеть может запутаться и придать больший вес тем признакам, которые имеют более высокое среднее значение, чем другие.
Мы реализуем этот шаг, импортируя метод StandardScaler из библиотеки sklearn.preprocessing. Мы создаем экземпляр переменной sc с помощью функции StandardScaler(). После чего мы используем функцию fittransform для реализации этих изменений в наборах данных Xtrain и Xtest. Наборы ytrain и y_test содержат двоичные значения, поэтому их не нужно стандартизировать. Теперь, когда наборы данных готовы, мы можем приступить к построению искусственной нейронной сети с использованием библиотеки Keras.
Построение искусственной нейронной сети
from keras.models import Sequential from keras.layers import Dense from keras.layers import Dropout
Теперь мы импортируем функции, которые будут использоваться для построения искусственной нейронной сети. Мы импортируем метод Sequential из библиотеки keras.models. Он будет использоваться для последовательного построения слоев обучения нейронных сетей. Следующим методом, который мы импортируем, будет функция Dense из библиотеки keras.layers.
Этот метод будет использоваться для построения слоев нашей искусственной нейронной сети.
classifier = Sequential()
Мы создаем экземпляр функции Sequential() в классификаторе переменных. Затем эта переменная будет использоваться для построения уровней обучения искусственной нейронной сети в python.
classifier.add(Dense(units = 128, kernel_initializer = 'uniform', activation = 'relu', input_dim = X.shape[1]))
Чтобы добавить слои в наш классификатор, мы используем функцию add(). Аргументом функции add является функция Dense(), которая в свою очередь имеет следующие аргументы:
Units: определяет количество узлов или нейронов в этом конкретном слое. Мы установили это значение на 128, что означает, что в нашем скрытом слое будет 128 нейронов.
Kernel_initializer: определяет начальные значения для весов различных нейронов в скрытом слое. Мы определили его как «uniform», что означает, что веса будут инициализированы значениями из равномерного распределения.
Activation: это функция активации для нейронов в конкретном скрытом слое. Здесь мы определяем функцию как rectified Linear Unit function или «relu».
Input_dim: определяет количество входов в скрытый слой, мы определили это значение равным количеству столбцов нашего фрейма данных входного объекта. Этот аргумент не потребуется в последующих слоях, так как модель будет знать, сколько выходных данных произведено предыдущим слоем.
classifier.add(Dense(units = 128, kernel_initializer = 'uniform', activation = 'relu'))
Затем мы добавляем второй слой с 128 нейронами, с единообразным инициализатором ядра и «relu» в качестве функции активации. Мы строим только два скрытых слоя в этой нейронной сети.
classifier.add(Dense(units = 1, kernel_initializer = 'uniform', activation = 'sigmoid'))
Следующий слой, который мы создадим, будет выходным, от него нам потребуется один выход. Следовательно, units равно 1, и в качестве функции активации выбрана сигмоида, поскольку мы хотим, чтобы прогноз представлял собой вероятность движения рынка вверх.
classifier.compile(optimizer = 'adam', loss = 'mean_squared_error', metrics = ['accuracy'])
Наконец, мы компилируем классификатор, передавая следующие аргументы:
Optimizer: Оптимизатором выбран «adam», который является продолжением стохастического градиентного спуска.
Loss: определяет потери, которые будут оптимизированы в течение периода обучения. Мы определяем их как среднеквадратическую ошибку.
Metrics: Определяет список метрик, которые будут оцениваться моделью на этапе тестирования и обучения. Мы выбрали точность в качестве нашей метрики оценки.
classifier.fit(X_train, y_train, batch_size = 10, epochs = 100)
Теперь нам нужно обучить созданную нами нейронную сеть нашим обучающим наборам данных. Это делается путем передачи Xtrain, ytrain, размера пакета и количества этапов в функцию fit(). Размер пакета относится к числу точек данных, которые модель использует для вычисления ошибки перед обратным распространением ошибок и внесением изменений в весовые коэффициенты. Количество этапов представляет количество раз обучения модели на обучающем наборе данных.
Благодаря этому наша искусственная нейронная сеть на Python была скомпилирована и готова делать прогнозы.
Прогнозирование движения цен акций
y_pred = classifier.predict(X_test) y_pred = (y_pred > 0.5)
Теперь, когда нейронная сеть скомпилирована, мы можем использовать метод predict() для прогнозирования. Мы передаем Xtest в качестве аргумента и сохраняем результат в переменной с именем ypred. Затем мы конвертируем ypred для хранения двоичных значений, сохраняя условие ypred> 5. Теперь переменная y_pred хранит либо True, либо False, в зависимости от того, было ли прогнозируемое значение больше или меньше 0,5.
dataset['y_pred'] = np.NaN dataset.iloc[(len(dataset) - len(y_pred)):,-1:] = y_pred trade_dataset = dataset.dropna()
Затем мы создаем новый столбец в dataframe с именем «ypred» и заполняем его значениями NaN. Затем мы сохраняем значения ypred в этом новом столбце, начиная со строк тестового набора данных. Это делается путем нарезки dataframe с использованием метода iloc, как показано в коде выше. Затем мы удаляем все значения NaN из набора данных и сохраняем их в новом dataframe с именем trade_dataset.
Расчет доходности стратегии
trade_dataset['Tomorrows Returns'] = 0.
trade_dataset['Tomorrows Returns'] = np.log(trade_dataset['Close']/trade_dataset['Close'].shift(1))
trade_dataset['Tomorrows Returns'] = trade_dataset['Tomorrows Returns'].shift(-1)
Теперь, когда у нас есть прогнозируемые значения движения акций, мы можем рассчитать доходность стратегии. Мы будем открывать длинную позицию, когда прогнозируемое значение у равно true, и будем открывать короткую позицию, когда прогнозируемый сигнал равен False.
Сначала мы вычисляем доходность, которую даст стратегия, если в конце сегодняшнего дня будет открыта длинная позиция, и закрыта в конце следующего дня. Мы начинаем с создания нового столбца с именем «Tomorrows Returns» в trade_dataset и сохраняем в нем значение 0. Мы используем десятичную запись, чтобы указать, что в этом новом столбце будут храниться значения с плавающей запятой. Далее, мы храним в нем логарифмическую доходность за сегодня, то есть логарифм цены закрытия сегодня, деленный на цену закрытия вчера. Затем мы смещаем эти значения вверх на один элемент, чтобы завтрашние доходы сохранялись при расчете сегодняшних.
trade_dataset['Strategy Returns'] = 0.
trade_dataset['Strategy Returns'] = np.where(trade_dataset['y_pred'] == True, trade_dataset['Tomorrows Returns'], - trade_dataset['Tomorrows Returns'])
Далее мы рассчитаем доходность стратегии. Мы создаем новый столбец под именем «StrategyReturns» и инициализируем его значением 0, чтобы указать хранение значений с плавающей запятой. Используя функцию np.where(), мы затем сохраняем в столбце «Strategy Returns» значение из столбца «Tomorrows Returns», если значение в столбце «ypred» хранит True (длинная позиция), иначе мы сохраняем отрицательное значение из столбца «Tomorrows Returns» (короткая позиция).
trade_dataset['Cumulative Market Returns'] = np.cumsum(trade_dataset['Tomorrows Returns'])
trade_dataset['Cumulative Strategy Returns'] = np.cumsum(trade_dataset['Strategy Returns'])
Теперь мы рассчитываем совокупную доходность как для рынка, так и для стратегии. Эти значения вычисляются с использованием функции cumsum(). Мы будем использовать накопленную сумму для построения графика доходности рынка и стратегии на последнем шаге.
Построение графика доходности
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.plot(trade_dataset['Cumulative Market Returns'], color='r', label='Market Returns')
plt.plot(trade_dataset['Cumulative Strategy Returns'], color='g', label='Strategy Returns')
plt.legend()
plt.show()
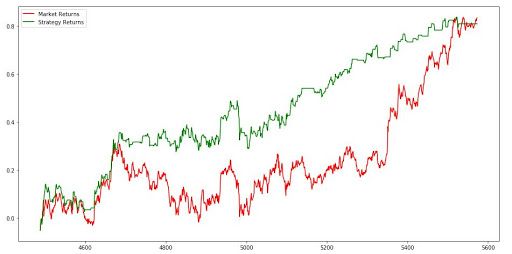
Теперь мы построим график доходности рынка и нашей стратегии, чтобы визуализировать работу нашей стратегии против рынка. Для этого мы импортируем matplotlib.pyplot. Затем мы используем функцию plot для построения графиков рыночных доходов и доходов и стратегии, используя кумулятивные значения, хранящиеся в dataframe trade_dataset. Затем мы создаем легенду и показываем график, используя функции legend() и show() соответственно.
График, показанный ниже, является выводом кода. Зеленая линия представляет доход, полученный с помощью стратегии, а красная линия представляет рыночный доход.
Заключение
Таким образом, когда мы подошли к концу нашей статьи, мы считаем, что теперь вы можете построить свою собственную искусственную нейронную сеть на Python и начать торговать, используя мощь и интеллект своих машин. Помимо нейронных сетей, есть много других моделей машинного обучения, которые можно использовать для торговли. Искусственная нейронная сеть или любая другая модель глубокого обучения будет наиболее эффективной, когда у вас есть более 100 000 точек данных для обучения модели.
Эта модель была разработана по ежедневным ценам, чтобы вы поняли, как построить модель. Для обучения модели рекомендуется использовать минутные или тиковые данные, что даст вам достаточно данных для эффективного обучения.







Комментариев нет:
Отправить комментарий