Перевод. Оригинал здесь.
Гистограммы очень часто используются для визуализации распределения независимых и зависимых переменных. Хотя базовая команда для построения гистограммы в R очень простая (hist()), для того чтобы привести гистограмму к тому виду, который вам нужен, необходимо знание хотя бы основных опций команды. Ниже я покажу несколько способов настройки гистограмм для своих нужд.
В начале хотелось бы отметить, что в R имеется пакет ggplot2, который обеспечивает продвинутые возможности для работы с графикой, в том числе и с гистограммами. Однако функция hist() входит в базовый набор R и проста в использовании, позволяя удовлетворить нужды большинства пользователей. Если же вам требуются возможности построения очень сложных гистограмм, рекомендую обратить внимание на ggplot2.
Итак, для наших целей я создам некоторый набор нормально распределенных данных. В R вы можете генерировать нормально распределенные данные с помощью функции rnorm():
> BMI<-rnorm m="24.2," n="1000," sd="2.2)</span">
Теперь у нас есть некоторый набор данных BMI, и простую гистограмму можно построить с помощью функции:
> hist(BMI)
По умолчанию R делает некоторые расчеты, прежде чем создать эту гистограмму, и я думаю, что было бы полезно вывести информацию, необходимую для понимания параметров этой гистограммы. Вы можете сделать это, сохранив гистограмму как объект, и затем вывести содержимое:
> histinfo<-hist br="">> histinfo
Вы получите следующий вывод:
> histinfo<-hist br="">> histinfo
Вы получите следующий вывод:
$breaks
[1] 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
$counts
[1] 1 7 25 31 85 129 149 185 175 108 63 31 8 2 1
$density
[1] 0.001 0.007 0.025 0.031 0.085 0.129 0.149 0.185 0.175 0.108 0.063 0.031 0.008 0.002 0.001
$mids
[1] 17.5 18.5 19.5 20.5 21.5 22.5 23.5 24.5 25.5 26.5 27.5 28.5 29.5 30.5 31.5
$xname
[1] "BMI"
$equidist
[1] TRUE
attr(,"class")
[1] "histogram"
Здесь вы можете видеть, как R решил по умолчанию разбить ваши данные. Показаны интервалы, плотность и средние значения для каждого интервала и так далее. Вы можете вывести любое из этих значений отдельно, например histinfo$counts.
Теперь мы можем использовать эту информацию для настройки нашего графика.
1. Количество интервалов
R выбирает, как разбить ваши данные, используя встроенный алгоритм, но вы можете при необходимости сделать это вручную несколькими способами. Используя опцию breaks(), вы можете просто задать количество ячеек гистограммы:
> hist(BMI, breaks=20, main="Breaks=20")
> hist(BMI, breaks=5, main="Breaks=5")
Интервалы не будут точно соответствовать заданному числу в связи с особенностями работы алгоритма, используемого R для разбивки данных. Если вы хотите задать точки разбиения абсолютно точно, можно немного видоизменить опцию breaks(), задав вектор из точек разбиения:
> hist(BMI, breaks=c(17,20,23,26,29,32), main="Breaks is vector of breakpoints")
> hist(BMI, breaks=c(17,20,23,26,29,32), main="Breaks is vector of breakpoints")
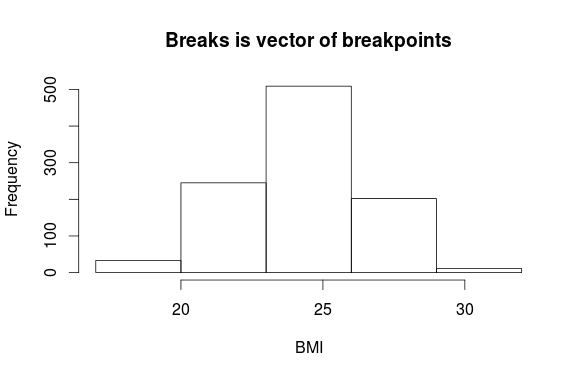
Эта команда указывает начальную и конечную точку для каждого интервала. Конечно, вы можете вы можете записать этот вектор в более краткой форме:
> hist(BMI, breaks=seq(17,32,by=3), main="Breaks is vector of breakpoints")
Обратите внимание, что по умолчанию R определяет для заданных точек закрытые справа (открытые слева) интервалы вида (a,b]. Вы можете изменить это с помощью опции right=FALSE, которая меняет вид интервалов на [a,b).
2. Частота vs плотность
Часто нас больше интересует плотность, чем частота, так как частота зависит от размера выборки. Вместо подсчета количества точек данных в интервале R может рассчитать плотности вероятности, используя опцию freq=FALSE:
> hist(BMI, freq=FALSE, main="Density plot")
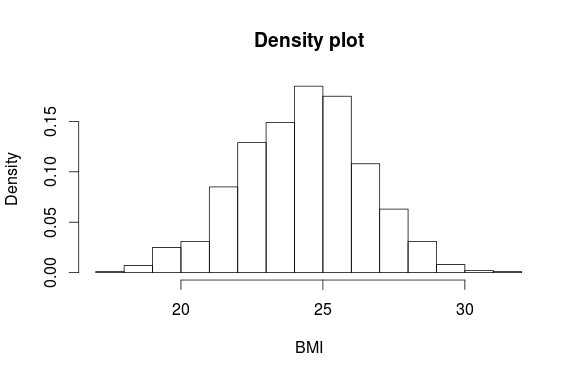
Обратите теперь внимание на ось y. Если границы интервалов равноудалены, с разностью конца и начала интервала, равной 1, то высота каждого прямоугольника пропорциональна количеству точек в интервале, и сумма плотностей вероятности будет равна 1. Здесь я задаю plot=FALSE, чтобы построить гистограмму, а не график, и показываю, что сумма всех плотностей вероятности равна 1:
> hist1<-hist plot="FALSE)<br">> hist1$density
[1] 0.001 0.007 0.025 0.031 0.085 0.129 0.149 0.185 0.175 0.108 0.063 0.031 0.008 0.002 0.001
> sum(hist1$density)
[1] 1
> sum(hist1$density)
[1] 1
Однако, если вы выберете интервалы таким образом, что их длина не всегда будет равна 1 (например breaks=c(17,25,26, 32)), то плошадь графика останется равной 1, но площадь прямоугольников будет представлять собой долю точек данных, попавших в интервал. Плотности вероятности рассчитываются как counts/(n*diff(breaks). При сложении площадей всех прямоугольников это дает единицу, то есть площадь прямоугольника рассчитывается путем умножения каждой плотности на длину соответствующего интервала:
> hist2<-hist breaks="c(17,25,26,32))<br" plot="FALSE,">> hist2$density
[1] 0.0765 0.1750 0.0355
> sum(hist2$density)
[1] 0.287
> sum(diff(hist2$breaks)*hist2$density)
[1] 1
3. Внешний вид гистограммы
И в конце мы улучшим внешний вид нашей гистограммы, проставив ее название, подписи осей, и раскрасив ее:
> hist(BMI, freq=FALSE, xlab="Body Mass Index",main="Distribution of Body Mass Index", col="lightgreen", xlim=c(15,35), ylim=c(0, .20))
[1] 0.0765 0.1750 0.0355
> sum(hist2$density)
[1] 0.287
> sum(diff(hist2$breaks)*hist2$density)
[1] 1
3. Внешний вид гистограммы
И в конце мы улучшим внешний вид нашей гистограммы, проставив ее название, подписи осей, и раскрасив ее:
> hist(BMI, freq=FALSE, xlab="Body Mass Index",main="Distribution of Body Mass Index", col="lightgreen", xlim=c(15,35), ylim=c(0, .20))
Здесь я задал подпись для оси x, изменил название гистограммы, раскрасил ее в светло-зеленый цвет и задал диапазоны для осей x и y.
И еще я могу добавить кривую нормального распределения для этого графика с помощью функции curve(), в которой я задам функцию нормального распределения плотности, среднее значение и стандартное отклонение моих данных, и добавлю эту кривую на предыдущий график, выбрав для нее синий цвет и линию толщиной 2.
> curve(dnorm(x, mean=mean(BMI), sd=sd(BMI)), add=TRUE, col="darkblue", lwd=2)
И еще я могу добавить кривую нормального распределения для этого графика с помощью функции curve(), в которой я задам функцию нормального распределения плотности, среднее значение и стандартное отклонение моих данных, и добавлю эту кривую на предыдущий график, выбрав для нее синий цвет и линию толщиной 2.
> curve(dnorm(x, mean=mean(BMI), sd=sd(BMI)), add=TRUE, col="darkblue", lwd=2)





Комментариев нет:
Отправить комментарий