Введение
PerformanceAnalytics - это библиотека функций, предназначенных для оценки эффективности и рисков финансовых активов или фондов. В частности, мы сосредоточили внимание на функциях, которые появились в научной литературе за последние несколько лет, но не имели функционального эквивалента в R.
Наша цель для PerformanceAnalytics - упростить оценку эффективности и рисков в рамках более широкого процесса принятия инвестиционных решений. Здесь нет волшебной пули - в этих метриках и графиках не будет одного правильного ответа. Инвестиции должны делаться в контексте инвестиционных целей. Но то, что эта библиотека стремится реализовать - помочь лицу, принимающему решения, собрать доказательства, чтобы ответить на конкретный вопрос, имеющий отношение к решению.
Эта статья обеспечивает демонстрацию некоторых возможностей PerformanceAnalytics. Мы фокусируемся на графиках и таблицах, но комментируем также некоторые другие показатели. Эти примеры не должны быть полными, но они должны обеспечить обзор видов анализа, которые могут быть выполнены.
Установка PerformanceAnalytics
Начиная с версии 0.9.4, PerformanceAnalytics доступен через CRAN, но вам понадобится версия 0.9.5 или новее, чтобы воспроизвести приведенные ниже примеры. Пользователи R могут просто ввести:
install.packages("PerformanceAnalytics")
Требуется несколько пакетов, включая Hmisc, zoo и различные пакеты Rmetrics, такие как fBasics, fCalendar и fExtremes. После установки PerformanceAnalytics загрузите его в активный сеанс R с помощью команды:
> library("PerformanceAnalytics")
Загрузка и просмотр данных
Сначала мы загрузим данные, используемые во всех приведенных ниже примерах. Как вы можете видеть, managers представляют собой набор данных, который содержит столбцы ежемесячной доходности для шести гипотетических управляющих активами (HAM1 - HAM6), индекс хедж-фонда EDHEC Long-Short Equity, общую доходность S&P500 и ряды общей доходности для 10-летней облигации Казначейства США и 3-месячного векселя. Ежемесячные доходности для всех рядов заканчиваются в декабре 2006 года и начинаются в разные периоды, начиная с января 1996 года. Аналогичные данные могут быть построены с использованием команды mymanagers=read.csv(«/path/to/file/mymanagers.csv», row.names = 1) , где первый столбец содержит даты в формате YYYY-MM-DD.
Примечание: эта библиотека применяется к доходностям (а не ценам), и была протестирована в основном на ежемесячном масштабе. Многие библиотечные функции будут работать с регулярными данными в разных масштабах (например, ежедневными, еженедельными и т. д.), или нерегулярными данными о доходностях. См. функцию CalculateReturns для расчета доходности от цен и помните, что функция aggregate библиотеки zoo имеет методы для классов данных tseries и zoo timeseries для рационального приведения нерегулярных данных к регулярным данным правильной периодичности.
> data(managers) > head(managers) HAM1 HAM2 HAM3 HAM4 HAM5 HAM6 EDHEC LS EQ SP500 TR US 10Y TR US 3m TR 1996-01-31 0.0074 NA 0.0349 0.0222 NA NA NA 0.0340 0.00380 0.00456 1996-02-29 0.0193 NA 0.0351 0.0195 NA NA NA 0.0093 -0.03532 0.00398 1996-03-31 0.0155 NA 0.0258 -0.0098 NA NA NA 0.0096 -0.01057 0.00371 1996-04-30 -0.0091 NA 0.0449 0.0236 NA NA NA 0.0147 -0.01739 0.00428 1996-05-31 0.0076 NA 0.0353 0.0028 NA NA NA 0.0258 -0.00543 0.00443 1996-06-30 -0.0039 NA -0.0303 -0.0019 NA NA NA 0.0038 0.01507 0.00412
Мы группируем вместе интересующие нас столбцы, чтобы упростить примеры. Как показано ниже, мы сначала подтверждаем размеры объекта и общую длину временных рядов.
Затем мы группируем столбцы вместе. В первом столбце HAM1 содержится объект нашего анализа в приведенных ниже примерах. Столбцы с двух до шести содержат доходность других менеджеров, использующих аналогичный стиль инвестирования, которые могут считаться заменителями - «одноранговой группой». Колонки семь и восемь содержат ключевые индексы. EDHEC Long/Short Equity index является «индексом равных» (peer index), индекс S&P500 Total Return является «индексом класса активов» (asset-class index).
Мы объединяем их в набор «индексов» для последующего анализа. Столбец девять мы в настоящее время пропускаем; столбец 10 мы используем в качестве ставки без риска для каждого месяца.
Затем мы делаем то же самое для интересующих нас строк. Мы вычисляем номера строк, которые представляют разные периоды ожидания, и сохраняем их удобными для проведения сравнительного анализа.
> dim(managers) [1] 132 10
> managers.length = dim(managers)[1] > colnames(managers) [1] "HAM1" "HAM2" "HAM3" "HAM4" "HAM5" "HAM6" "EDHEC LS EQ" "SP500 TR" [9] "US 10Y TR" "US 3m TR"
> manager.col = 1 > peers.cols = c(2,3,4,5,6) > indexes.cols = c(7,8) > Rf.col = 10
> trailing12.rows = ((managers.length - 11):managers.length) > trailing12.rows [1] 121 122 123 124 125 126 127 128 129 130 131 132
> trailing36.rows = ((managers.length - 35):managers.length) > trailing60.rows = ((managers.length - 59):managers.length) > frInception.rows = (length(managers[,1]) - length(managers[,1][!is.na(managers[,1])]) + 1):length(managers[,1])
Создание графиков и таблиц для презентаций
Графики и диаграммы помогают визуализировать информацию. Наши цели при разработке этих функций заключались в упрощении процесса создания хорошо отформатированных диаграмм, которые часто используются для анализа портфеля, и для создания графики полиграфического качества, которая может использоваться в документах. Графические возможности R обширны, но простота графических функций по умолчанию, таких как plot, не всегда сравнима с графикой, предоставляемой коммерческим программным обеспечением для анализа портфеля, таким как MorningStar или PerTrac.
Цветовые палитры
Мы создали некоторые специфические цветовые палитры, предназначенные для создания читаемых специализированных линейных диаграмм и гистограмм. Мы используем этот подход (вместо того, чтобы генерировать их «на лету») по двум причинам: во-первых, при этом меньше зависимостей от библиотек, которые не нужно вызывать динамически; и, во-вторых, чтобы гарантировать цвет, используемый для n-го столбца данных. На рис. 1 показаны примеры различных палитр.
Первая категория наборов цветов предназначена для того, чтобы сосредоточить внимание на первостепенных данных, и включают redfocus, bluefocus и greenfocus. Эти палитры лучше всего использовать, когда есть важный набор данных. Другие данные предоставляют некоторый контекст, поэтому они отображаются в градациях серого. Они были сгенерированы с помощью RColorBrewer, используя палитру «серых» уровня 8 и заменяя темно-серый. Чтобы скоординировать эти цвета с равноценными цветами ниже, замените цвет выделения первым цветом равноценной палитры снизу. Это будет координировать вместе различные графики.
Вторая категория - это наборы равноценных цветов. Эти цветовые решения полезны, когда все данные должны быть выведены и быть различимы на линейном графике. Различные цифры в названии указывают количество генерируемых цветов (шесть цветов, вероятно, являются максимальными для читаемой линейки, но мы предоставляем целых двенадцать). Примерами являются rainbow12equal - rainbow4equal, с шагом в два. Эти цвета были сгенерированы командой rainbow(12, s = 0.6, v = 0.75). rich12equal и другие соответствующие наборы цветов были сгенерированы с помощью функции rich.colors(12) пакета gplots.
Аналогичным образом были созданы tim12equall и подобные ему наборы цветов, функцией tim.colors (12) пакета fields, функцией, созданной для эмуляции цветового набора Matlab. Наборы цветов The dark8equal, dark6equal, set8equal и set6equal были созданы с помощью пакета RColorBrewer, например, brewer.pal(8,"Dark2").
Третья категория - это набор монохромных наборов цветов, включая greenmono, bluemono, redmono, gray8mono и gray6mono.
Чтобы увидеть, что содержат эти списки, просто введите имя.
> tim12equal [1] "#00008F" "#0000EA" "#0047FF" "#00A2FF" "#00FEFF" "#5AFFA5" "#B5FF4A" "#FFED00" "#FF9200" "#FF3700" "#DB0000" "#800000"
Это просто списки строк, которые содержат коды RGB каждого цвета. Вы можете легко создать свой собственный список, если у вас есть особая палитра, которую вы любите использовать. Кроме того, вы можете использовать цвета по умолчанию R. Для получения дополнительной информации см.
Рис.1 Примеры цветовых палитр
Символы
Аналогично, есть несколько наборов сгруппированных символов для диаграмм рассеяния. Они включают opensymbols, closedsymbols, fillsymbols, linesymbols и allsymbols.
Расположение легенды
В отдельных диаграммах легенда может перемещаться вокруг графика. Есть девять мест, которые могут быть указаны по ключевому слову: «rightright», «bottom», «bottomleft», «left», «topleft», «top», «topright», «right» и «center». Они помещают легенду в данном месте. Дополнительную информацию можно найти в xy.coord. Большинство составных диаграмм имеют фиксированные местоположения легенд.
Другие параметры
Мы попытались оставить доступ ко всему обширному списку параметров, доступных в традиционной графике R. Для получения дополнительной информации см. plot.default и par. В приведенном выше примере мы передали lwd значение 2, которое влияет на ширину линии. Мы также можем изменить тип линии или другие параметры.
Создание графиков и таблиц
Теперь мы готовы анализировать наш набор данных. Этот раздел начинается с набора диаграмм, которые предоставляют обзор эффективности, некоторые таблицы для представления данных и основных статистических данных, а затем мы обсудим способы сравнения распределений, относительной эффективности и снижения рисков.
Создание графиков эффективности
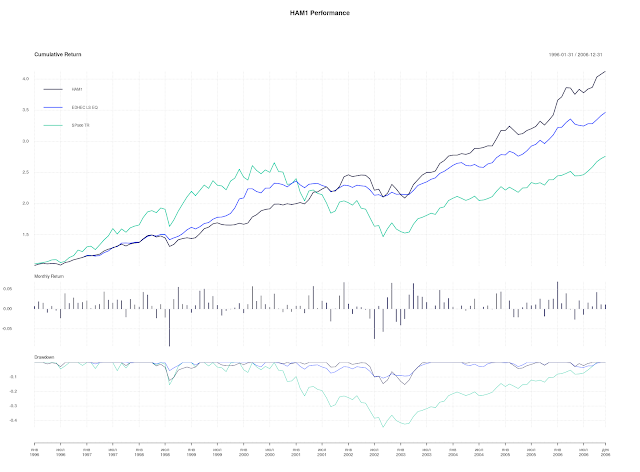
На рисунке 2 показана сводная диаграмма эффективности с тремя панелями и код, используемый для ее создания. Верхняя диаграмма представляет собой нормальную совокупную диаграмму доходности (или индекса капитала), которая показывает совокупную доходность во времени для каждого столбца. Для данных с более поздними временами начала работы установите параметр begin = "axis", который строит доходности для всех столбцов с 1 или begin = "first", который строит доходность каждого столбца, начиная со значения доходности первого столбца данных. Вторая из этих настроек, которая по умолчанию, позволяет читателю увидеть, как будут сравниваться два индекса, если бы они запускались одновременно, независимо от начального периода. Кроме того, ось y может быть сделана логарифмической, так что рост можно сравнивать в течение длительного периода времени. Эта диаграмма может генерироваться независимо с помощью chart.CumReturns.
> charts.PerformanceSummary(managers[,c(manager.col,indexes.cols)], colorset=rich6equal, lwd=2, ylog=TRUE)
На втором графике показаны индивидуальные ежемесячные доходы, наложенные на скользящую ожидаемую меру риска, называемую Cornish Fisher Value-at-Risk (VaR) или модифицированная VaR. Альтернативные меры риска, включая стандартное отклонение (заданное как StdDev) и традиционная Value-at-Risk (VaR), могут быть заданы с использованием параметра method. Обратите внимание, что StdDev и VaR являются симметричными. Модифицированная VaR, с другой стороны, является асимметричной и нарисована только нижняя граница. Эти расчеты риска производятся для скользящего значения, или могут быть рассчитаны в окне прокрутки путем установки width в значение количества периодов. Эти расчеты должны помочь читателю идентифицировать события или периоды, когда оценки ожидаемого риска могут внезапно измениться или помочь оценить, как выглядят предположения, лежащие в основе расчета. Расчеты рисков могут быть сгенерированы для всех столбцов с помощью параметра all. Если установлено значение TRUE, функция вычисляет линии риска для каждого указанного столбца и может помочь читателю оценить относительные уровни риска во времени. Эта диаграмма может быть сгенерирована с использованием chart.BarVaR.
Третий график в серии - это просадка, которая показывает уровень потерь от последнего значения достигнутого пикового дохода. Каждый раз, когда кумулятивная доходность опускается ниже максимальной совокупной прибыли, это просадка. Эта диаграмма помогает читателю оценить синхронность периодов потерь и их сравнительную величину. Как и следовало ожидать, эту диаграмму можно также создать с помощью chart.Drawdown.
Создание таблицы месячных прибылей
Итоговая статистика - это необходимое агрегирование и сокращение (потенциально тысяч) периодических прибылей. Обычно эти статистические данные лучше воспринимаются при организации в таблицу связанных статистических данных, сгруппированных для определенной цели. Общее представление прошлых прибылей, организованных по месяцам и накапливаемых по календарному году, обычно представляется в виде таблицы, например, в table.CalendarReturns.
На рисунке 3 показана таблица доходностей, отформатированных по годам в строках, месяцам в столбцах и общей прибыли в последнем столбце. Для дополнительных столбцов будут добавляться годовые доходы в виде столбцов. Добавление контрольных показателей наряду с годовыми данными полезно для сравнения результатов за календарные годы. Поскольку в примере есть несколько столбцов, мы упрощаем чтение, используя функцию t для транспонирования результирующего data frame.
> t(table.CalendarReturns(managers[,c(manager.col,indexes.cols)])) 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 янв 0.7 2.1 0.6 -0.9 -1.0 0.8 1.4 -4.1 0.5 0.0 6.9 фев 1.9 0.2 4.3 0.9 1.2 0.8 -1.2 -2.5 0.0 2.1 1.5 мар 1.6 0.9 3.6 4.6 5.8 -1.1 0.6 3.6 0.9 -2.1 4.0 апр -0.9 1.3 0.8 5.1 2.0 3.5 0.5 6.5 -0.4 -2.1 -0.1 мая 0.8 4.4 -2.3 1.6 3.4 5.8 -0.2 3.4 0.8 0.4 -2.7 июн -0.4 2.3 1.2 3.3 1.2 0.2 -2.4 3.1 2.6 1.6 2.2 июл -2.3 1.5 -2.1 1.0 0.5 2.1 -7.5 1.8 0.0 0.9 -1.4 авг 4.0 2.4 -9.4 -1.7 3.9 1.6 0.8 0.0 0.5 1.1 1.6 сен 1.5 2.2 2.5 -0.4 0.1 -3.1 -5.8 0.9 0.9 2.6 0.7 окт 2.9 -2.1 5.6 -0.1 -0.8 0.1 3.0 4.8 -0.1 -1.9 4.3 ноя 1.6 2.5 1.3 0.4 1.0 3.4 6.6 1.7 3.9 2.3 1.2 дек 1.8 1.1 1.0 1.5 -0.7 6.8 -3.2 2.8 4.4 2.6 1.1 HAM1 13.6 20.4 6.1 16.1 17.7 22.4 -8.0 23.7 14.9 7.8 20.5 EDHEC LS EQ NA 21.4 14.6 31.4 12.0 -1.2 -6.4 19.3 8.6 11.3 11.7 SP500 TR 23.0 33.4 28.6 21.0 -9.1 -11.9 -22.1 28.7 10.9 4.9 15.8
Рис 3: Создание таблицы календарных прибылей
Расчет месячных статистических данных
Аналогично, таблица статистики ежемесячных прибылей на рисунке 4 была создана для одновременного отображения совокупности связанных показателей для сравнения по набору инструментов или фондов. В этом примере мы смотрим на эффективность «с самого начала» для большинства менеджеров, поэтому при интерпретации результатов необходимо уделять внимание отсутствующим данным или неравным временным промежуткам. Большинство людей предпочтут такую статистику для аналогичных периодов. Каждая из отдельных функций может быть вызвана индивидуально. Когда мы начали этот проект, мы обсуждали, будут ли такие таблицы полезными или нет. Мы просто предлагаем их как отправную точку для создания ваших собственных таблиц. Добавляйте, удаляйте, делайте то, что вам кажется полезным. Если вы считаете, что ваша работа может быть полезной для других, попробуйте поделиться ею, чтобы мы могли включить ее в будущую версию этой библиотеки.
> table.Stats(managers[,c(manager.col,peers.cols)]) HAM1 HAM2 HAM3 HAM4 HAM5 HAM6 Observations 132.0000 125.0000 132.0000 132.0000 77.0000 64.0000 NAs 0.0000 7.0000 0.0000 0.0000 55.0000 68.0000 Minimum -0.0944 -0.0371 -0.0718 -0.1759 -0.1320 -0.0404 Quartile 1 0.0000 -0.0098 -0.0054 -0.0198 -0.0164 -0.0016 Median 0.0112 0.0082 0.0102 0.0138 0.0038 0.0128 Arithmetic Mean 0.0111 0.0141 0.0124 0.0110 0.0041 0.0111 Geometric Mean 0.0108 0.0135 0.0118 0.0096 0.0031 0.0108 Quartile 3 0.0248 0.0252 0.0314 0.0460 0.0309 0.0255 Maximum 0.0692 0.1556 0.1796 0.1508 0.1747 0.0583 SE Mean 0.0022 0.0033 0.0032 0.0046 0.0052 0.0030 LCL Mean (0.95) 0.0067 0.0076 0.0062 0.0019 -0.0063 0.0051 UCL Mean (0.95) 0.0155 0.0206 0.0187 0.0202 0.0145 0.0170 Variance 0.0007 0.0013 0.0013 0.0028 0.0021 0.0006 Stdev 0.0256 0.0367 0.0365 0.0532 0.0457 0.0238 Skewness -0.6588 1.4580 0.7908 -0.4311 0.0738 -0.2800 Kurtosis 2.3616 2.3794 2.6829 0.8632 2.3143 -0.3489
Рис 4: Создание таблицы статистики
Сравнение распределений
Для анализа распределений могут оказаться полезными несколько графиков. Результат chart.Boxplot, показанный на рисунке 5, является примером графики, которую сложно создать в Excel и которая в результате недостаточно используется. Однако boxplot прибылей - это очень полезный способ наблюдать форму больших коллекций прибылей активов таким образом, чтобы их было легко сравнивать друг с другом. При оценке инвестиций часто бывает полезно узнать, соответствует ли рассматриваемый вами инструмент нормальному распределению. Один из первых способов определить, насколько близко актив относится к нормальному или лог-нормальному распределению - это визуально оценить ваши данные. Как chart.QQPlot, так и chart.Histogram быстро даст вам представление о том, смотрите ли вы на нормально распределенную историю прибылей. На рисунке 6 показана гистограмма, созданная для HAM1 с различными опциями отображения.
Оглянитесь на результаты, сгенерированные table.Stats. Различия между var и SemiVariance помогут вам определить коэффициент ассиметрии в прибылях. Коэффициент ассимметрии (skewness) измеряет степень асимметрии в распределении прибылей. Положительная асимметрия указывает на то, что больше прибылей положительны, отрицательная асимметрия свидетельствует о том, что больше прибылей отрицательны. Инвестор должен в большинстве случаев предпочесть позитивно искаженный актив аналогичному (стиль, отрасль, регион) активу с отрицательной асимметрией. Коэффициент эксцесса (kurtosis) измеряет концентрацию прибылей в любой заданной части распределения (как вы можете видеть на гистограмме). Функция [fBasics]kurtosis по умолчанию возвращает то, что называется “избыточным kurtosis”, где ноль является нормальным распределением, другие методы вычисления kurtosis, где нет опции method="excess", задают нормальное распределение со значением 3. В целом рациональный инвестор должен предпочесть активом с низким отрицательным коэффициентом эксцесса, это будет означать более прогнозируемую доходность. Если Вам необходимо проанализировать распределение сложных или негладких распределений активов, пакет nortest имеет несколько продвинутых статистических тестов для анализа нормальности распределения.
Относительная доходность и риск
Доходность и риск могут быть пересчитаны в годовом выражении, чтобы упростить сравнение в течение более длительных периодов времени. Такое агрегирование является популярным, поскольку предлагает опорную точку для сравнения, как например, на рисунке 7. Примеры в Return.annualized, StdDev.annualized и SharpeRatio.annualized.
chart.Scatter - это диаграмма рассеяния с некоторыми дополнительными атрибутами, которые используются в chart.RiskReturnScatter. Могут использоваться различные параметры риска. Метод может быть любым из modVaR, VaR или StdDev.
Также может быть наложена дополнительная информация. Если для add.sharpe установлено значение, например c(1,2,3), функция накладывает линию отношения Шарпа, которая показывает уровни отношения Шарпа, от одного до трех. Линии рисуются с пересечением оси y для безрискового отношения (rf) и наклона соответствующего уровня отношения Шарпа. Строки следует удалять, если они не подходят (например, sharpe.ratio = NULL). При наличии большого количества активов (или столбцов) могут мешать имена. Чтобы удалить их, установите add.names = NULL. box plot может быть добавлен к полям, чтобы помочь идентифицировать относительный уровень эффективности, для этого задайте add.boxplots = TRUE.
> chart.Boxplot(managers[ trailing36.rows, c(manager.col, peers.cols, indexes.cols)], main = "Trailing 36-Month Returns")
Рис. 5: Создание Boxplot
> layout(rbind(c(1,2),c(3,4))) > chart.Histogram(managers[,1,drop=F], main = "Plain", methods = NULL) > chart.Histogram(managers[,1,drop=F], main = "Density", breaks=40, methods = c("add.density", "add.normal")) > chart.Histogram(managers[,1,drop=F], main = "Skew and Kurt", methods = c("add.centered", "add.rug")) > chart.Histogram(managers[,1,drop=F], main = "Risk Measures", methods = c("add.risk"))
Рис. 6: Создание гистограмм доходности.> chart.RiskReturnScatter(managers[trailing36.rows,1:8], Rf=.03/12, main = "Trailing 36-Month Performance", colorset=c("red", rep("black",5), "orange", "green"))
Рис. 7: Вывод относительного риска и доходности
Проверка стабильности прибылей
Скользящая эффективность обычно используется в качестве способа оценки стабильности потока прибылей. Хотя, возможно, она не получила большого распространения в финансовой литературе из-за ее происхождения из обработки цифровых сигналов, многие практики считают, что скользящая эффективность является полезным способом изучения и сегментации эффективности и риска. См. функцию Chart.RollingPerformance, которая позволяет отображать разные показатели за скользящие периоды времени.
На рис. 8 показаны три графика, первый для скользящей прибыли, второй - для скользящего стандартного отклонения, а третий - для скользящего коэффициента Шарпа. Эти три диаграммы строятся с помощью отдельных вызовов Chart.RollingPerformance с различными аргументами FUN.
Отображение относительной эффективности
Функция chart.RelativePerformance показывает отношение совокупной эффективности для двух активов в каждый момент времени и позволяет легко видеть периоды низкой или низкой эффективности. Значение на диаграмме менее важно, чем наклон линии. Если наклон положительный, первый актив (числитель) превосходит второй, и наоборот. На рисунке 9 показаны прибыли менеджера, о котором идет речь, относительно каждого члена группы и индекса группы.
Рассматривая данные по-другому, мы используем один и тот же график для оценки отдельных партнеров по индексу класса активов. На рисунке 10 показаны прибыли членов группы относительно S&P500. Может возникнуть несколько вопросов: кто превосходит S&P? Могут ли они сделать это постоянно? Существуют ли циклы, когда они отстают или превосходят группу? Какой из менеджеров лучше всех?
Измерение относительной эффективности по отношению к эталону
Определение и использование контрольного показателя может помочь нам объяснить, насколько хорошо мы отвечаем нашим инвестиционным целям. Тест может помочь нам объяснить, насколько хорошо управляются портфели, оценить полученный риск и желаемую прибыль и проверять, что цели были соблюдены. Контрольные показатели используются для лучшего контроля над процессом управления инвестициями.
Современная теория портфеля представляет собой набор инструментов и методов, с помощью которых не склонный к риску инвестор может построить оптимальный портфель. Она охватывает модель ценообразования капитальных активов (CAPM), гипотезу эффективного рынка и все формы количественного построения и оптимизации портфеля. CAPM обеспечивает обоснование пассивного или индексного инвестирования, полагая, что активы, которые не находятся на эффективной границе, будут либо расти, либо снижаться в цене, пока они не окажутся на эффективной границе рыночного портфеля.
> charts.RollingPerformance(managers[, c(manager.col, peers.cols, indexes.cols)], Rf=.03/12, colorset = c("red", rep("darkgray",5), "orange", "green"), lwd = 2)
Рис. 8: Оценка скользящей эффективности
> chart.RelativePerformance(managers[ , manager.col, drop = FALSE], managers[ , c(peers.cols, 7)], colorset = tim8equal[-1], lwd = 2, legend.loc = "topleft")
Рис. 9: Оценка относительной эффективности активов
> chart.RelativePerformance(managers[ , c(manager.col, peers.cols) ], managers[, 8, drop=F], colorset = rainbow8equal, lwd = 2, legend.loc = "topleft")
Рис. 10: Оценка эффективности по отношению к эталону
Премия за эффективность, обеспечиваемая инвестициями по пассивной стратегии (эталон), предоставляется функцией ActivePremium, которая представляет собой годовой доход от инвестиций за вычетом годовой доходности эталона. Близкой мерой является TrackingError, которая измеряет необъясненную часть эффективности инвестиций по сравнению с эталоном. InformationRatio инвестиций в рамках MPT или CAPM - это ActivePremium, деленная на TrackingError. InformationRatio может использоваться для ранжирования инвестиций соответствующим образом.
Код на рисунке 11 создает таблицу статистики, связанной с CAPM, которую мы можем просмотреть и сравнить показатели менеджеров. Обратите внимание, что мы ориентируемся на скользящий 36-месячный период. В дополнение к перечисленным имеется множество других метрик, связанных с CAPM. CAPM.RiskPremium на инвестиции - это показатель того, насколько эффективность актива отличается от ставки без риска. Отрицательная премия за риск обычно указывает, это плохая инвестиция, а деньги должны быть переведены на безрисковый актив или на другой актив с более высокой премией за риск. CAPM.alpha - это степень, в которой прибыли активов получаются по причинам, не связанными с рынком. И наоборот, CAPM.beta описывает части прибыли актива, которые могут быть напрямую связаны с доходностью пассивной инвестиции в базовый актив.
Линия Capital Market в CAPM.CML связывает избыточный ожидаемый доход от эффективного рыночного портфеля с его риском (представленный в CAPM функцией StdDev). Наклон CML, CAPM.CML.slope, является коэффициентом Шарпа для рыночного портфеля. Линия Security Market Line построена путем вычисления строки CAPM.RiskPremium над CAPM.beta. Для эталонного актива это будет 1 над премией за риск базового актива. Наклон SML, в основном для целей построения, задается CAPM.SML.slope. CAPM - модель рыночного равновесия, но обычно она применяется к равновесным портфелям, которые могут создавать (иногда серьезные) проблемы в оценке. Подобным образом, как мы показали ранее, мы можем смотреть на стабильность параметров линейной модели во времени. На рис. 12 показана трехмерная диаграмма для альфа-, бета-и r-квадратов. Каждая диаграмма вызывает chart.RollingRegression с другим параметром метода.
Аналогично, мы можем оценить, является ли корреляция между двумя временными рядами постоянной во времени. На рисунке 13 показана скользящая 12-месячная корреляция между каждой из одноранговой групп и S&P500. Чтобы посмотреть на отношения во времени и сделать снимок статистической релевантности меры, используйте table.Correlation, как показано на рисунке 14.
> table.CAPM(managers[trailing36.rows, c(manager.col, peers.cols)], managers[ trailing36.rows, 8, drop=FALSE], Rf = managers[ trailing36.rows, Rf.col, drop=FALSE]) HAM1 to SP500 TR HAM2 to SP500 TR HAM3 to SP500 TR HAM4 to SP500 TR HAM5 to SP500 TR HAM6 to SP500 TR Alpha 0.0051 0.0020 0.0020 0.0009 0.0002 0.0022 Beta 0.6267 0.3223 0.6320 1.1282 0.8755 0.8150 Beta+ 0.8227 0.4176 0.8240 1.8430 1.0985 0.9993 Beta- 1.1218 -0.0483 0.8291 1.2223 0.5283 1.1320 R-squared 0.3829 0.1073 0.4812 0.3444 0.5209 0.4757 Annualized Alpha 0.0631 0.0247 0.0243 0.0109 0.0030 0.0271 Correlation 0.6188 0.3276 0.6937 0.5868 0.7218 0.6897 Correlation p-value 0.0001 0.0511 0.0000 0.0002 0.0000 0.0000 Tracking Error 0.0604 0.0790 0.0517 0.1073 0.0583 0.0601 Active Premium 0.0384 -0.0260 -0.0022 0.0154 -0.0077 0.0138 Information Ratio 0.6363 -0.3295 -0.0428 0.1433 -0.1319 0.2296 Treynor Ratio 0.1741 0.1437 0.1101 0.0768 0.0734 0.1045
Рис. 11: Создание таблицы статистики, связанной с CAPM
> charts.RollingRegression(managers[, c(manager.col, peers.cols), drop = FALSE], managers[, 8, drop = FALSE], Rf = .03/12, colorset = redfocus, lwd = 2)
Рис. 12: Создание скользящей регрессии
> chart.RollingCorrelation(managers[,c(manager.col, peers.cols)], managers[, 8, drop = FALSE], colorset = tim8equal, lwd = 2, main = "12-Month Rolling Correlation")
Рис. 13: График скользящей корреляции
> table.Correlation(managers[, c(manager.col, peers.cols)], managers[, 8, drop = F], legend.loc = "lowerleft") Correlation p-value Lower CI Upper CI HAM1 to SP500 TR 0.6600671 7.397842e-18 0.55138376 0.7467191 HAM2 to SP500 TR 0.4128282 1.715350e-06 0.25576240 0.5486602 HAM3 to SP500 TR 0.6608633 6.545409e-18 0.55236590 0.7473433 HAM4 to SP500 TR 0.5601846 2.870109e-12 0.43052170 0.6671932 HAM5 to SP500 TR 0.2844487 1.216830e-02 0.06458459 0.4779755 HAM6 to SP500 TR 0.5091542 1.735968e-05 0.30101889 0.6709863
Рис. 14: Расчет корреляций
Расчет снижения риска
Многие активы, включая хедж-фонды, товары, опционы и даже наиболее распространенные акции, в течение достаточно длительного периода времени, не следуют нормальному распределению. Для таких не нормально распределенных активов для адекватной модели риска требуется более сложный подход, чем стандартное отклонение/волатильность.
Марковиц в своей нобелевской речи и в нескольких документах предположил, что SemiVariance (полудисперсия) будет лучшей мерой риска, чем дисперсия. Эта мера также называется SemiDeviation. Более общий случай отклонения реализуется в функции DownsideDeviation, предложенной Sortino и Price (1994), где минимально приемлемый доход (MAR) является параметром функции. Интересно отметить, что дисперсия и средний доход могут обеспечить гладкий эллиптический эффективный рубеж для оптимизации портфеля с использованием [quadprog]solve.QP или [tseries]portfolio.optim или [fPortfolio]MarkowitzPortfolio. Использование полудисперсии или многих других мер риска не обязательно создаст гладкий эллипс, что вызовет значительные дополнительные трудности для менеджера портфеля, пытающегося построить оптимальный портфель. Мы оставим более полный разбор и внедрение методов оптимизации портфеля на другой раз.
Другими очень широко используемыми мерами снижения риска являются анализ просадок или потери от достигнутого пикового значения. Самый простой способ - проверить maxDrawdown, так как это скажет вам худшую совокупную потерю, когда-либо происходившую с активом. Если вы хотите посмотреть все просадки, вы можете использовать table.Drawdowns для поиска и сортировки в порядке от наихудшего до наименьшего, как показано на рисунке 16.
Функция UpDownRatios может дать вам некоторое представление о влиянии асимметрии и эксцесса доходов и дать вам понять, как длина и величина перемещений вверх или вниз сравниваются друг с другом. Или, как упоминалось выше, вы также можете вывести просадки с помощью chart.Drawdown.
> table.DownsideRisk(managers[,1:6],Rf=.03/12) HAM1 HAM2 HAM3 HAM4 HAM5 HAM6 Semi Deviation 0.0191 0.0201 0.0237 0.0395 0.0324 0.0175 Gain Deviation 0.0169 0.0347 0.0290 0.0311 0.0313 0.0149 Loss Deviation 0.0211 0.0107 0.0191 0.0365 0.0324 0.0128 Downside Deviation (MAR=10%) 0.0178 0.0164 0.0214 0.0381 0.0347 0.0161 Downside Deviation (Rf=3%) 0.0154 0.0129 0.0185 0.0353 0.0316 0.0133 Downside Deviation (0%) 0.0145 0.0116 0.0174 0.0341 0.0304 0.0121 Maximum Drawdown 0.1518 0.2399 0.2894 0.2874 0.3405 0.0788 Historical VaR (95%) -0.0258 -0.0294 -0.0425 -0.0799 -0.0733 -0.0341 Historical ES (95%) -0.0513 -0.0331 -0.0555 -0.1122 -0.1023 -0.0392 Modified VaR (95%) -0.0342 -0.0276 -0.0368 -0.0815 -0.0676 -0.0298 Modified ES (95%) -0.0610 -0.0614 -0.0440 -0.1176 -0.0974 -0.0390
Рис. 15: Создание таблицы статистики просадок
> table.Drawdowns(managers[,1,drop=F]) From Trough To Depth Length To Trough Recovery 1 2002-02-28 2003-02-28 2003-07-31 -0.1518 18 13 5 2 1998-05-31 1998-08-31 1999-03-31 -0.1239 11 4 7 3 2005-03-31 2005-04-30 2005-09-30 -0.0412 7 2 5 4 2001-09-30 2001-09-30 2001-11-30 -0.0312 3 1 2 5 1996-04-30 1996-07-31 1996-08-31 -0.0284 5 4 1
Рис. 16: Создание таблицы отсортированных просадок









Комментариев нет:
Отправить комментарий