Введение
«Время» является наиболее важным фактором, обеспечивающим успех в бизнесе. Трудно идти в ногу со временем. Но технология разработала несколько мощных методов, используя которые мы можем «видеть вещи» раньше времени. Не волнуйтесь, я не говорю о машине времени. Давайте будем реалистами!
Я говорю о методах прогнозирования. Одним из таких методов, который работает с данными на основе времени, является моделирование временных рядов. Как следует из названия, он включает в себя работу с данными, основанными на времени (годы, дни, часы, минуты), чтобы получить скрытую информацию для принятия обоснованного решения.
Модели временных рядов являются очень полезными, когда у вас есть последовательно коррелированные данные. Большинство бизнес-клиентов работают с данными временных рядов, чтобы проанализировать количество продаж на следующий год, посещаемость веб-сайта, конкурентную позицию и многое другое. Однако это также одна из областей, которую многие аналитики не понимают.
Поэтому, если вы не уверены в полном знании процесса моделирования временных рядов, это руководство познакомит вас с различными уровнями моделирования временных рядов и связанными с ними методами.
1. Основы - моделирование временных рядов
Давайте начнем с основ. Сюда входят стационарные ряды, случайные блуждания, коэффициент Ро, критерий стационарности Дики-Фуллера. Если эти термины вас пугают, не волнуйтесь - они прояснятся через некоторое время, и я уверен, что вы начнете наслаждаться этим предметом.
Стационарный ряд
Существует три основных критерия для ряда, который может быть классифицирован как стационарный ряд:
1. Среднее значение ряда не должно быть функцией времени, а должно быть константой. Изображение ниже включает левый график, удовлетворяющий условию стационарности, тогда как красный график имеет среднее значение, меняющееся во времени.
2. Дисперсия ряда не должна быть функцией времени. Это свойство известно как гомоскедастичность. Следующий график показывает, что является, а что не является стационарным рядом (обратите внимание на изменяющийся разброс на правом графике).
3. Ковариация i-го члена и (i + m)-го члена не должна зависеть от времени. На следующем графике вы заметите, что спрэд становится уже с увеличением времени. Следовательно, для «красного ряда» ковариация не постоянна во времени.
Почему меня волнует «стационарность» временного ряда?
Причина, по которой я сначала занялся этим термином, заключалась в том, что до тех пор, пока ваш временной ряд не станет стационарным, вы не сможете построить модель временных рядов. В тех случаях, когда критерий стационарности нарушается, первым условием становится стационаризация временного ряда, а затем попытка с помощью стохастических моделей предсказать этот временной ряд. Есть несколько способов достижения стационарности. Некоторые из них - детрендинг, разности и т. д.
Случайные блуждания
Это базовая концепция временного ряда. Возможно, вы хорошо знаете эту концепцию. Но я видел много людей в отрасли, которые интерпретируют случайные блуждания как стационарный процесс. В этом разделе с помощью математики я сделаю эту концепцию кристально ясной. Давайте рассмотрим пример.
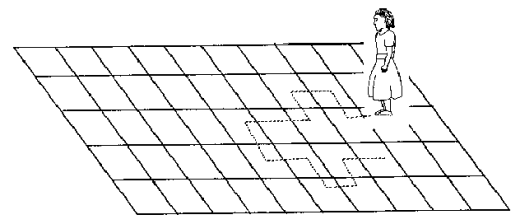
Пример: представьте себе девушку, которая случайно движется на гигантской шахматной доске. В этом случае следующая позиция девушки зависит только от последней позиции.
(источник: http://scifun.chem.wisc.edu/WOP/RandomWalk.html)
А теперь представьте, что вы сидите в другой комнате и не можете видеть девушку. Вы хотите предсказать положение девушки во временем. Насколько точными будут ваши прогнозы? Конечно, вы будете становиться все более и более неточными, поскольку положение девушки меняется. При t = 0 вы точно знаете, где девушка. В следующий раз она может двигаться только на 8 квадратов, и, следовательно, ваша вероятность угадать падает до 1/8 вместо 1, и она продолжает снижаться. Теперь давайте попробуем сформулировать этот ряд:
X(t) = X(t-1) + Er(t)
где Er(t) - ошибка в момент времени t. Это случайность, которую девушка приносит в каждый момент времени.
Теперь, если мы рекурсивно обозначим все X, мы в конечном итоге получим следующее уравнение:
X(t) = X(0) + Sum(Er(1),Er(2),Er(3).....Er(t))
Теперь давайте попробуем проверить наши предположения о стационарных рядах по этой формулировке случайного блуждания:
1. Является ли среднее значение постоянным?
E[X(t)] = E[X(0)] + Sum(E[Er(1)],E[Er(2)],E[Er(3)].....E[Er(t)])
Мы знаем, что математическое ожидание любой ошибки будет нулевым, поскольку оно является случайным.
Отсюда получаем E[X(t)] = E[X(0)] = Constant.
2. Является ли дисперсия постоянной?
Var[X(t)] = Var[X(0)] + Sum(Var[Er(1)],Var[Er(2)],Var[Er(3)].....Var[Er(t)])
Var[X(t)] = t * Var(Error) = Зависимость от времени.
Таким образом, мы делаем вывод, что случайное блуждание не является стационарным процессом, поскольку его дисперсия зависит от времени. Кроме того, если мы проверим ковариацию, мы увидим, что она также зависит от времени.
Мы уже знаем, что случайное блуждание - нестационарный процесс. Давайте введем новый коэффициент в уравнение, чтобы посмотреть, сможем ли мы сделать его формулировку стационарной.
Вводим коэффициент: Rho
X(t) = Rho * X(t-1) + Er(t)
Теперь мы будем изменять значение Rho, чтобы посмотреть, сможем ли мы сделать ряд стационарным. Здесь мы будем интерпретировать разброс визуально и не будем проверять стационарность.
Начнем с идеально стационарного ряда с Rho = 0. Вот график для временного ряда:
Увеличение значения Rho до 0,5 дает нам следующий график:
Вы можете заметить, что наши циклы стали шире, но, по сути, здесь нет серьезного нарушения допущений стационарности. Давайте теперь возьмем более экстремальный случай Rho = 0,9
Мы все еще видим, что X возвращается от крайних значений к нулю через некоторые интервалы. Эта серия также существенно не нарушает нестационарность. Теперь давайте взглянем на случайные блуждания с rho = 1.
Это очевидно является нарушением стационарных условий. Что делает rho = 1 частным случаем, который плохо проходит тест на стационарность? Мы найдем этому математическую причину.
Давайте возьмем мат. ожидание от каждой стороны уравнения “X(t) = Rho * X(t-1) + Er(t)”
E[X(t)] = Rho *E[ X(t-1)]
Это уравнение имеет глубокий смысл. Следующий X (или x в момент времени t) приближается к Rho*Последнее значение X.
Например, если X (t - 1) = 1, E [X (t)] = 0,5 (для Rho = 0,5). Теперь, если X движется в любом направлении от нуля, он возвращается к нулю на следующем шаге. Единственный компонент, который может продвинуть его еще дальше, это ошибка. Ошибка с одинаковой вероятностью пойдет в любом направлении. Что происходит, когда Rho становится 1? Никакая сила не может потянуть X вниз на следующем шаге.
Тест Дики-Фуллера на стационарность
То, что вы только что узнали, формально известно как тест Дики-Фуллера. Вот небольшой твик, который может быть сделан для нашего уравнения, чтобы преобразовать его в тест Дики Фуллера:
X(t) = Rho * X(t-1) + Er(t)
X(t) - X(t-1) = (Rho - 1) X(t - 1) + Er(t)
Мы должны проверить, отличается ли Rho-1 от нуля или нет. Если нулевая гипотеза будет отвергнута, мы получим стационарный временной ряд.
Тестирование стационарности и преобразование ряда в стационарный являются наиболее важными процессами моделирования временных рядов. Вам нужно запомнить каждую деталь этой концепции, чтобы перейти к следующему этапу моделирования временных рядов.
Давайте теперь рассмотрим пример, чтобы показать вам, как выглядит временной ряд.
2. Исследование временных рядов в R
Здесь мы научимся обрабатывать временные ряды в R. Наша область будет ограничена исследованием данных в наборе данных временных рядов, а не переходом к построению моделей временных рядов.
Я использовал встроенный набор данных R под названием AirPassengers. Набор данных состоит из ежемесячных итоговых данных о пассажирах международных рейсов за 1949–1960 годы.
Загрузка набора данных
Ниже приведен код, который поможет вам загрузить набор данных и вывести несколько метрик верхнего уровня.
#Это говорит нам, что ряд данных имеет формат временного ряда
> data(AirPassengers) > class(AirPassengers) [1] "ts"
# Это начало временного ряда
> start(AirPassengers) [1] 1949 1
# Это конец временного ряда
> end(AirPassengers) [1] 1960 12
# Цикл этого временного ряда составляет 12 месяцев в году
> frequency(AirPassengers) [1] 12
> summary(AirPassengers) Min. 1st Qu. Median Mean 3rd Qu. Max. 104.0 180.0 265.5 280.3 360.5 622.0
Подробные метрики
#Количество пассажиров распределяется по спектру
> plot(AirPassengers)
#Строим график временного ряда
> abline(reg=lm(AirPassengers~time(AirPassengers)))
Вот еще несколько операций, которые вы можете сделать:
> cycle(AirPassengers)
#Эта команда напечатает цикл по годам
> plot(aggregate(AirPassengers,FUN=mean))
#Эта команда агрегирует циклы и отображает годовой тренд
> boxplot(AirPassengers~cycle(AirPassengers))
#График за несколько месяцев даст нам представление о сезонном эффекте
Важные выводы
Годовой тренд ясно показывает, что количество пассажиров постоянно растет.
Дисперсия и среднее значение в июле и августе намного выше, чем в остальные месяцы.
Несмотря на то, что среднее значение каждого месяца сильно отличается, их дисперсия невелика. Следовательно, мы имеем сильный сезонный эффект с циклом 12 месяцев или меньше.
Исследование данных становится наиболее важным в модели временных рядов - без этого исследования вы не узнаете, является ли ряд стационарным или нет. Как и в этом случае, мы уже знаем много деталей о модели, которую мы ищем.
Давайте теперь рассмотрим несколько моделей временных рядов и их характеристики. Мы также продолжим эту проблему и сделаем несколько прогнозов.
3. Введение в моделирование временных рядов ARMA
Модели ARMA обычно используются при моделировании временных рядов. В модели ARMA AR обозначает авторегрессию, а MA обозначает скользящую среднюю. Если эти слова звучат для вас устрашающе, не беспокойтесь - я разложу вам эти концепции по полочкам в ближайшие несколько минут! Но прежде чем мы начнем, вы должны помнить, что AR или MA не применимы к нестационарным рядам.
В случае, если вы получаете нестационарный ряд, вам сначала необходимо сделать ряд стационарным, а затем выбрать одну из доступных моделей временных рядов.
Сначала я объясню каждую из этих двух моделей (AR и MA) по отдельности. Далее мы рассмотрим характеристики этих моделей.
Авторегрессионная модель временных рядов
Давайте разберемся в моделях AR, используя пример ниже:
Текущий ВВП страны, скажем, x(t) зависит от ВВП прошлого года, то есть x(t - 1). Гипотеза заключается в том, что общая стоимость производства продуктов и услуг в стране в финансовом году (известная как ВВП) зависит от создания заводов/услуг в предыдущем году и вновь созданных отраслей/заводов/услуг в текущем году. Но основной компонент ВВП - предыдущий год.
Следовательно, мы можем формально написать уравнение ВВП как:
x(t) = alpha * x(t – 1) + error (t)
Это уравнение известно как формулировка AR(1). Цифра один (1) обозначает, что следующий экземпляр зависит исключительно от предыдущего экземпляра. alpha - это коэффициент, который мы ищем, чтобы минимизировать функцию ошибок. Обратите внимание, что x(t-1) действительно связан с x(t-2) таким же образом. Следовательно, любой скачек по x(t) будет постепенно исчезать в будущем.
Например, допустим, x(t) - это количество бутылок с соком, проданных в городе в определенный день. В течение зимы очень немногие покупали бутылки сока. Внезапно в определенный день температура повысилась, и спрос на бутылки сока взлетел до 1000. Однако через несколько дней снова похолодало. Но, зная, что люди привыкли пить сок в жаркие дни, 50% людей все еще пили сок в холодные дни. В последующие дни доля снизилась до 25% (50% от 50%), а затем постепенно до небольшого числа после значительного количества дней. Следующий график объясняет свойство инерции серии AR:
Модель временного ряда скользящей средней
Давайте рассмотрим другой случай, чтобы понять модель временного ряда скользящей средней.
Производитель производит сумку определенного типа, которая легко доступна на рынке. В связи с конкурентным рынком, продажа сумок в течение многих дней стояла на нуле. Однажды производитель провел некоторый эксперимент с дизайном и изготовил сумку другого типа. Этот тип сумки был ограниченно доступен на рынке. Таким образом, он смог продать весь запас в 1000 сумок (назовем это x (t)). Спрос стал настолько высоким, что на складе закончился товар. В результате около 100 клиентов не смогли приобрести эту сумку. Давайте назовем этот гэп ошибкой в этот момент времени. Со временем сумка потеряла свой вау-фактор. Но все еще осталось немного клиентов, которые ушли с пустыми руками в предыдущий день. Ниже приводится простая формулировка для изображения этого сценария:
x(t) = beta * error(t-1) + error (t)
Если мы попробуем построить этот график, он будет выглядеть примерно так:
Вы заметили разницу между моделью MA и AR? В модели MA шум/шок быстро исчезают со временем. Модель AR демонстрирует продолжительный эффект от скачка.
Разница между моделями AR и MA
Основное различие между моделями AR и MA основано на корреляции между объектами временных рядов в разные моменты времени. Корреляция между x (t) и x (t-n) для n больше порядка МА всегда равна нулю. Это напрямую вытекает из того факта, что ковариация между x(t) и x(t-n) равна нулю для моделей MA. Однако в модели AR корреляция x(t) и x(t-n) уменьшается постепенно с ростом n. Эта разница используется независимо от наличия модели AR или модели MA. График корреляции может дать нам порядок модели МА.
Использование графиков ACF и PACF
Как только мы получим стационарный временной ряд, мы должны ответить на два основных вопроса:
Q1. Это процесс AR или MA?
Q2. Какой порядок процессов AR или MA нам нужно использовать?
Подсказка для решения этих вопросов уже есть в предыдущем разделе. Вы не заметили?
На первый вопрос можно ответить, используя Total Correlation Chart (также известный как функция автокорреляции/ACF). ACF представляет собой график общей корреляции между различными функциями запаздывания. Например, в проблеме ВВП, ВВП в момент времени t равен x(t). Нас интересует корреляция x(t) с x(t-1), x(t-2) и так далее. Теперь давайте подумаем над тем, что мы узнали выше.
В рядах скользящих средних lag n мы не получим никакой корреляции между x(t) и x(t - n -1). Следовательно, total correlation chart обрывается с n-м запаздыванием. Таким образом, становится просто найти запаздывание для ряда МА. Для ряда AR эта корреляция будет постепенно снижаться без какого-либо предельного значения. Так что же нам делать, если это ряд AR?
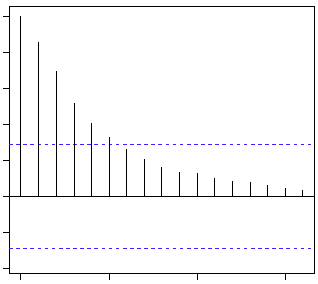
Вот вторая подсказка. Если мы обнаружим частичную корреляцию каждого лага, он будет отсечен после степени ряда AR. Например, если у нас есть ряд AR(1), если мы исключаем эффект 1-го лага (x (t-1)), наш 2-й лаг (x (t-2)) не зависит от x (t). Следовательно, функция частичной корреляции (PACF) резко упадет после 1-го лага. Ниже приведены примеры, которые прояснят ваши сомнения по поводу этой концепции:
Синяя линия выше показывает значительно отличающиеся от нуля значения. Очевидно, что график выше имеет обрезание кривой PACF после 2-го лага, что означает, что это в основном процесс AR(2).
Очевидно, что график выше имеет обрезание кривой ACF после 2-го лага, что означает, что это в основном процесс MA(2).
До сих пор мы рассматривали, как идентифицировать тип стационарных рядов, используя графики ACF и PACF. Теперь я познакомлю вас с комплексной структурой для построения модели временных рядов. Кроме того, мы также обсудим практическое применение моделирования временных рядов.
4. Фреймворк и применение моделирования временных рядов ARIMA
К этому моменту мы узнали основы моделирования временных рядов в R и ARMA. Сейчас самое время объединить к эти части.
Обзор фреймворка
Этот фреймворк (показанный ниже) определяет пошаговый подход к процессу: «Как проводить анализ временных рядов»:
Как вы помните, первые три шага уже обсуждались выше. Тем не менее, то же самое кратко описано ниже:
Шаг 1. Визуализация временного ряда
Важно проанализировать тенденции до построения любой модели временных рядов. Детали, которые нас интересуют, касаются любых тенденций, сезонности или случайного поведения в ряде. Мы рассмотрели эту часть во второй части этой статьи.
Шаг 2: Стационарность ряда
Как только мы узнаем закономерности, тренды, циклы и сезонность, мы можем проверить, является ли ряд стационарным или нет. Тест Дики - Фуллера является одним из наиболее популярных тестов, чтобы проверить стационарность. Мы рассмотрели этот тест в первой части этой серии статей. Что, если ряд окажется нестационарным?
Существует три часто используемых метода, чтобы сделать временные ряды стационарными:
1. Детрендинг: здесь мы просто удаляем компонент тренда из временного ряда. Например, уравнение моего временного ряда:
x(t) = (mean + trend * t) + error
Мы просто удалим эту часть в скобках и построим модель для всего остального.
2. Нахождение разностей: это обычно используемая техника для устранения нестационарности. Здесь мы пытаемся смоделировать разности величин, а не сами величины. Например,
x(t) – x(t-1) = ARMA (p , q)
Эта разность называется частью интеграции в AR(I)MA. Теперь у нас есть три параметра
p : AR
d : I
q : MA
3. Сезонность: Сезонность легко может быть включена непосредственно в модель ARIMA. Подробнее об этом сказано ниже.
Шаг 3: Поиск оптимальных параметров
Параметры p, d, q можно найти, используя графики ACF и PACF. Дополнение к этому подходу может состоять в том, что если и ACF, и PACF постепенно уменьшаются, это указывает на то, что нам нужно сделать временной ряд стационарным и ввести значение «d».
Шаг 4: Строим модель ARIMA
Имея в руках параметры, мы можем теперь попытаться построить модель ARIMA. Значение, найденное в предыдущем разделе, может быть приблизительной оценкой, и нам нужно изучить больше комбинаций (p, d, q). Вариант с самым низким BIC и AIC должен быть нашим выбором. Мы также можем попробовать некоторые модели с сезонной составляющей. На всякий случай мы отмечаем любую сезонность на участках ACF/PACF.
Шаг 5: Делаем прогнозы
Получив окончательную модель ARIMA, мы готовы делать прогнозы на будущие временные точки. Мы также можем визуализировать тренды для перекрестной проверки, если модель работает нормально.
Применение модели временных рядов
Здесь мы будем использовать тот же пример, который мы использовали выше. Затем, используя временные ряды, мы сделаем прогнозы на будущее. Мы рекомендуем вам проверить пример, прежде чем продолжать.
С чего мы начинаем?
Ниже приводится график количества пассажиров по годам. Попробуйте сделать наблюдения на этом графике, прежде чем двигаться дальше в статье.
Вот мои наблюдения:
1. Существует трендовый компонент, который увеличивает количество пассажиров год от года.
2. Похоже, что сезонный компонент имеет цикл менее 12 месяцев.
3. Дисперсия в данных продолжает расти со временем.
Мы знаем, что нам нужно решить две проблемы, прежде чем тестировать стационарные ряды. Во-первых, нам нужно удалить неравные дисперсии. Мы делаем это, используя логарифм ряда. Во-вторых, нам нужно рассмотреть компонент тренда. Мы делаем это, беря разницу в ряду. Теперь давайте проверим полученный ряд.
adf.test(diff(log(AirPassengers)), alternative="stationary", k=0)
Расширенный тест Дики-Фуллера
data: diff(log(AirPassengers)) Dickey-Fuller = -9.6003, Lag order = 0, p-value = 0.01 alternative hypothesis: stationary
Мы видим, что ряды достаточно стационарны, чтобы выполнять любые виды моделирования временных рядов.
Следующий шаг - найти правильные параметры, которые будут использоваться в модели ARIMA. Мы уже знаем, что компонент «d» равен 1, так как нам нужно 1 разность, чтобы сделать ряд стационарным. Мы делаем это с помощью графиков корреляции. Ниже приведены графики ACF для ряда:
#Графики ACF
acf(log(AirPassengers))
Что вы видите на графике, показанном выше?
Ясно, что убывание графика ACF очень медленное, что означает, что выборка не является стационарной. Мы уже обсуждали выше, что теперь мы намерены подгонять разность логарифмов, а не логарифм напрямую. Давайте посмотрим, как получаются кривые ACF и PACF после регрессии разности.
[stextbox id="grey"]
acf(diff(log(AirPassengers)))
pacf(diff(log(AirPassengers)))
Очевидно, что график ACF обрезается после первого лага. Следовательно, значение p должно быть 0, так как ACF - это кривая, дающая обрезание. В ир же время значение q должно быть 1 или 2. После нескольких итераций мы обнаружили, что комбинация значений (p, d, q) (0,1,1) оказывается комбинацией с наименьшим AIC и BIC.
Давайте возьмем модель ARIMA и спрогнозируем будущие 10 лет. Также мы постараемся вписать сезонный компонент в состав ARIMA. Затем мы визуализируем прогноз вместе с обучающими данными. Вы можете использовать следующий код, чтобы сделать то же самое:
(fit <- arima(log(AirPassengers), c(0, 1, 1),seasonal = list(order = c(0, 1, 1), period = 12)))
pred <- predict(fit, n.ahead = 10*12)
ts.plot(AirPassengers,2.718^pred$pred, log = "y", lty = c(1,3))
Заключение
Мы подошли к концу руководства по моделированию временных рядов. Я надеюсь, что он поможет вам улучшить ваши знания, чтобы работать с данными, основанными на времени. Чтобы извлечь максимальную пользу из этого учебного пособия, я бы посоветовал вам попрактиковаться в R и проверить свои успехи.





















Комментариев нет:
Отправить комментарий