Были ли вы в ситуации, когда вы ожидали, что ваша модель машинного обучения должна работать очень хорошо, но у нее была низкая точность? Вы проделали всю тяжелую работу - так где же модель классификации сработала не так? Как это исправить?
Существует множество способов оценить эффективность вашей модели классификации, но ни один из них не выдержал испытания временем, кроме матрицы ошибок. Она помогает нам оценить, как наша модель работала, где она пошла не туда, и предлагает нам рекомендации по исправлению нашего пути.
В этой статье мы рассмотрим, как матрица ошибок дает целостное представление об эффективности вашей модели. И, в отличие от названия, вы поймете, что матрица ошибок - довольно простая, но мощная концепция. Итак, давайте раскроем тайну матрицы ошибок!
Что такое матрица ошибок?
Вопрос на миллион долларов - что такое, в конце концов, матрица ошибок?
Матрица ошибок - это матрица размером N x N, используемая для оценки эффективности модели классификации, где N - количество целевых классов. Матрица сравнивает фактические целевые значения с предсказанными моделью машинного обучения. Это дает нам целостное представление о том, насколько хорошо работает наша классификационная модель и какие ошибки она допускает.
Для задачи двоичной классификации у нас будет матрица 2 x 2, как показано ниже, с 4 значениями:
Расшифруем матрицу:
- Целевая переменная имеет два значения: положительное или отрицательное.
- Столбцы представляют фактические значения целевой переменной.
- Строки представляют собой прогнозируемые значения целевой переменной.
Но подождите - что здесь TP, FP, FN и TN? Это важнейшая часть матрицы ошибок. Давайте разберемся с каждым термином ниже.
Понимание True Positive, True Negative, False Positive и False Negative в матрице ошибок
True Positive (TP)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было положительным, и модель предсказала положительное значение.
True Negative (TN)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было отрицательным, и модель предсказала отрицательное значение.
False Positive (FP) - ошибка 1-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было отрицательным, но модель предсказала положительное значение.
- Также известна как ошибка 1-го типа.
False Negative (FN) - ошибка 2-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было положительным, но модель предсказала отрицательное значение.
- Также известна как ошибка 2-го типа.
Позвольте мне привести пример, чтобы лучше это понять. Предположим, у нас есть набор данных классификации с 1000 точками данных. Мы подгоняем на нем классификатор и получаем следующую матрицу ошибок:
Различные значения матрицы ошибок будут следующими:
- True Positive (TP) = 560; это означает, что 560 положительных точек данных были правильно классифицированы моделью.
- True Negative (TN) = 330; это означает, что 330 отрицательных точек данных были правильно классифицированы моделью.
- False Positive (FP) = 60; это означает, что 60 отрицательных точек данных были неправильно классифицированы моделью как положительные.
- False Negative (FN) = 50; это означает, что 50 положительных точек данных были неправильно классифицированы моделью как отрицательные.
Это оказался довольно приличный классификатор для нашего набора данных, учитывая относительно большее количество истинно положительных и истинно отрицательных значений.
Помните об ошибках 1-го и 2-го типа. Интервьюеры любят спрашивать, в чем разница между ними!
Зачем нам нужна матрица ошибок?
Прежде чем ответить на этот вопрос, давайте подумаем о проблеме гипотетической классификации.
Допустим, вы хотите предсказать, сколько людей инфицировано заразным вирусом, до того, как у них проявятся симптомы, и изолировать их от здорового населения. Двумя значениями для нашей целевой переменной будут: Sick и Not Sick.
Теперь вы, должно быть, задаетесь вопросом - зачем нам матрица ошибок, когда у нас есть наш вечный друг - Точность? Что ж, посмотрим, где точность не работает.
Наш набор данных является примером несбалансированного набора данных. Имеется 947 точек данных для отрицательного класса и 3 точки данных для положительного класса. Вот как мы рассчитаем точность:
Посмотрим, как работает наша модель:
Общие значения результатов:
TP = 30, TN = 930, FP = 30, FN = 10
Итак, точность для нашей модели:
96%! Неплохо!
Но это дает неверное представление о результате. Подумайте об этом.
Наша модель гласит: «Я могу предсказать заболевание в 96% случаев». Однако она делает наоборот. Это предсказание людей, которые не заболеют с точностью 96%, пока больные распространяют вирус!
Как вы думаете, это правильный показатель для нашей модели, учитывая серьезность проблемы? Разве мы не должны измерять, сколько положительных случаев мы можем правильно предсказать, чтобы остановить распространение заразного вируса? Или, из правильно спрогнозированных случаев сколько положительных случаев для проверки надежности нашей модели?
Здесь мы сталкиваемся с двойным понятием «точность (Precision) и полнота (Recall)».
Precision vs. Recall
Точность говорит нам, сколько из правильно предсказанных случаев действительно оказались положительными.
Вот как рассчитать точность:
Это определило бы надежность нашей модели.
Полнота сообщает нам, сколько реальных положительных случаев мы смогли правильно предсказать с помощью нашей модели.
А вот как мы можем рассчитать полноту:
Мы можем легко рассчитать точность и полноту для нашей модели, подставив значения в приведенные выше уравнения:
50% процентов правильно предсказанных случаев оказались положительными. В то время как 75% положительных результатов были успешно предсказаны нашей моделью. Потрясающие!
Точность - полезный показатель в тех случаях, когда ложноположительный результат важнее, чем ложноотрицательный.
Точность важна в системах рекомендаций по музыке или видео, на веб-сайтах электронной коммерции и т. д. Неправильные результаты могут привести к оттоку клиентов и нанести вред бизнесу.
Полнота - полезный показатель в случаях, когда ложноотрицательный результат важнее ложноположительного.
Полнота важна в медицинских случаях, когда не имеет значения, что возникает ложная тревога, но реальные положительные случаи не должны оставаться незамеченными!
В нашем примере полнота была бы лучшим показателем, потому что мы не хотим, чтобы случайно выписали инфицированного человека и позволили ему смешаться со здоровым населением, тем самым распространяя заразный вирус. Теперь вы можете понять, почему точность была плохим показателем для нашей модели.
Но будут случаи, когда нет четкой разницы между тем, что важнее: точность или полнота. Что нам делать в таких случаях? Мы их совмещаем!
F1-Score
На практике, когда мы пытаемся повысить точность нашей модели, полнота снижается, и наоборот. F1-Score отражает обе тенденции в одном значении:
F1-Score представляет собой гармоничное среднее значение точности и полноты, поэтому дает общее представление об этих двух показателях. Оно максимально, когда точность равно полноте.
Но здесь есть одна загвоздка. Интерпретируемость оценки F1 оставляет желать лучшего. Это означает, что мы не знаем, чего добивается наш классификатор - точности или полноты? Итак, мы используем его в сочетании с другими оценочными метриками, что дает нам полную картину результата.
Матрица ошибок с использованием scikit-learn в Python
Вы знаете теорию - теперь давайте применим ее на практике. Давайте запрограммируем матрицу ошибок с помощью библиотеки Scikit-learn (sklearn) на Python.
# confusion matrix in sklearn
from sklearn.metrics import confusion_matrix
3 from sklearn.metrics import classification_report
# actual values
actual = [1,0,0,1,0,0,1,0,0,1]
# predicted values
predicted = [1,0,0,1,0,0,0,1,0,0]
# confusion matrix
matrix = confusion_matrix(actual,predicted, labels=[1,0])
print('Confusion matrix : \n',matrix)
# outcome values order in sklearn
tp, fn, fp, tn = confusion_matrix(actual,predicted,labels=[1,0]).reshape(-1)
print('Outcome values : \n', tp, fn, fp, tn)
# classification report for precision, recall f1-score and accuracy
matrix = classification_report(actual,predicted,labels=[1,0])
print('Classification report : \n',matrix)
Sklearn имеет две отличные функции: confusion_matrix() и classification_report().
Sklearn confusion_matrix() возвращает значения матрицы ошибок. Однако результат немного отличается от того, что мы изучили до сих пор. Она принимает строки как фактические значения, а столбцы как прогнозные значения. В остальном концепция осталась прежней.
Sklearn classes_report() выводит точность, полноту и f1-score для каждого целевого класса. В дополнение к этому, она также имеет некоторые дополнительные значения: micro avg, macro avg и weighted avg.
Mirco average - это оценка точности/полноты/f1, рассчитанная для всех классов.
Macro average - это среднее значение точности/полноты/f1-score.
Weighted average - это просто средневзвешенное значение точности/полноты/f1-score.
Матрица ошибок для мультиклассовой классификации
Как матрица ошибок будет работать для задачи классификации нескольких классов? Мы рассмотрим и этот случай.
Давайте нарисуем матрицу ошибок для мультиклассовой задачи, в которой мы должны предсказать, любит ли человек Facebook, Instagram или Snapchat. Матрица ошибок будет иметь вид 3 x 3:
true positive, true negative, false positive и false negative для каждого класса будут вычисляться путем сложения значений ячеек следующим образом:
Вот и все! Вы готовы расшифровать любую матрицу ошибок размером N x N!
Заключение
И вдруг матрица ошибок перестает быть такой запутанной! Эта статья должна дать вам прочную основу для интерпретации и использования матрицы ошибок для алгоритмов классификации в машинном обучении.
Вскоре мы выпустим статью о кривой AUC-ROC и продолжим наше обсуждение там. До этого не теряйте надежды на свою модель классификации, возможно, вы просто используете неправильную метрику оценки!





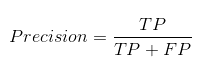








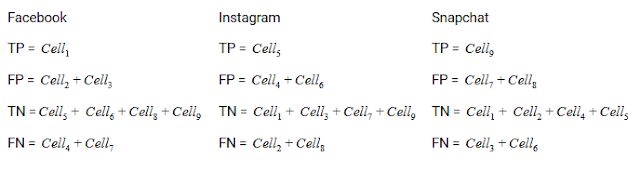
Комментариев нет:
Отправить комментарий