Оригинал: Time Series and Spectral Analysis
Многие экологические, эпидемиологические и физические данные представлены в виде временных рядов. Временной ряд - это последовательность наблюдений, записанных через последовательные интервалы времени.
В целом временные ряды характеризуются зависимостью. Значение ряда в некоторый момент времени t обычно не зависит от его значения, скажем, в t − 1. Мы используем специализированную статистику для анализа временных рядов и специализированные структуры данных для их представления в R. Эти структуры данных значительно облегчают наш последующий анализ.
Эти заметки представляют собой очень короткое введение в некоторые инструменты, которые я нашел полезными для экологии болезней.
Некоторые определения
Временной ряд
Временной ряд - это набор данных, индексированных по времени. Например {yt: t = 1,2,… n}. Diggle (1990) отмечает, что наблюдения не обязательно должны быть равномерно распределены и что «более честное» обозначение может быть {y(ti): t = 1,2,… n}.
Автоковариация
Временные ряды обычно характеризуются некоторой степенью последовательной зависимости наблюдений друг от друга. Эту зависимость можно измерить с помощью автоковариации, которая представляет собой просто ковариацию между двумя элементами ряда:
Функция автокорреляции (ACF)
ACF - это мера линейной предсказуемости ряда. Это коэффициент корреляции Пирсона между элементами временного ряда, например, временами ss и tt.
Функция взаимной корреляции (CCF)
CCF - это линейная зависимость одного ряда yt от некоторого другого ряда xs:
где
это взаимная ковариация.
Временные ряды в R
В R есть класс для данных временных рядов с регулярным интервалом (ts), но требование регулярного интервала весьма ограничено. Данные об эпидемиях часто нерегулярны. Более того, формат дат, связанных с отчетными данными, может сильно различаться. Пакет zoo (что означает “Z’s ordered observations”) обеспечивает поддержку данных с нерегулярным интервалом, в которых используется произвольный формат упорядочения.
Используйте данные о приповерхностной температуре HadCRUT4 из Сборника данных наблюдений Центра Хэдли для северного полушария, предоставленные Метеорологическим бюро Великобритании.
Даты в этом файле данных находятся в первом столбце в формате yyyy/mm. Нам нужно разделить их на переменную года и переменную месяца. Используйте команду substr() для анализа yr и mo как отдельных переменных.
library(zoo)
HC4nh <- read.table("https://web.stanford.edu/class/earthsys214/data/HadCRUT.4.2.0.0.monthly_nh.txt",
header=FALSE)
yr <- substr(HC4nh$V1,1,4)
mo <- substr(HC4nh$V1,6,7)
dates <- as.Date(paste(yr,mo,'01',sep="-"))
## function to standardize (z-score)
stand <- function(x) {
y <- (x - mean(x,na.rm=TRUE))/sd(x,na.rm=TRUE)
return(y)
}
# Create zoo object for satandardised anomalies:
NH <- zoo(stand(HC4nh$V2),order.by=dates)
plot(NH,main="",ylab="Standardized Temp (Z)",xlab="Year")acf(coredata(NH),lag.max = 240, main="Temperature is Highly Autocorrelated!")Спектральный анализ
Многие временные ряды показывают периодическое поведение. Это периодическое поведение может быть очень сложным. Спектральный анализ - это метод, который позволяет нам обнаруживать лежащие в основе периодичности. Чтобы выполнить спектральный анализ, мы сначала должны преобразовать данные из временной области в частотную.
Технические детали спектрального анализа выходят далеко за рамки этих заметок. Классическим источником является Priestly (1981), но существует множество других. Вкратце, ковариация временного ряда может быть представлена функцией, известной как спектральная плотность. Спектральную плотность можно оценить с помощью объекта, известного как периодограмма, который представляет собой квадрат корреляции между нашим временным рядом и синусоидальными/косинусоидальными волнами на разных частотах, охватываемых рядом (Venables & Ripley 2002).
При больших n периодограмма приблизительно независима для разных частот. Эту независимость можно улучшить, так же как и визуальное качество и интерпретируемость графика, путем сглаживания периодограммы с использованием ядра сглаживания (которое обычно представляет собой своего рода взвешенное скользящее среднее).
Простой пример
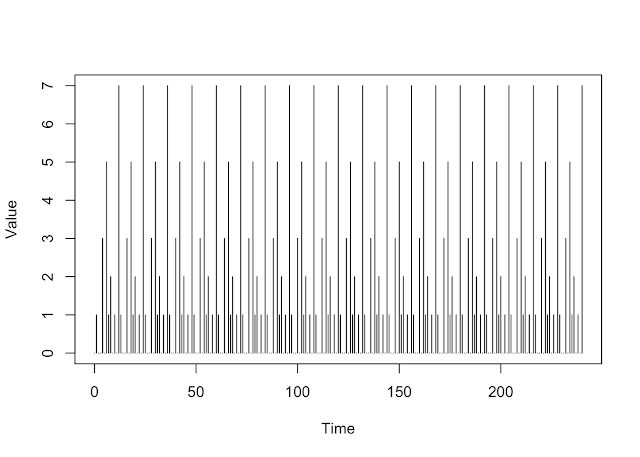
Слабый сигнал каждые три года; более крупный сигнал каждые четыре года; большой сигнал каждые шесть лет.
y1 <- rep(c(1,0,0),80)
y2 <- rep(c(0,0,0,2),60)
y3 <- rep(c(0,0,0,0,0,5),40)
y <- y1+y2+y3
plot(0:240, c(0,y), type="h", xlab="Time", ylab="Value")Теперь вычислите частотный спектр «вручную», используя функцию быстрого преобразования Фурье, fft. Этот код взят из превосходной книги Shumway & Stoffer (2017) по анализу временных рядов в R. Обычно, когда мы работаем с реальными данными мы просто используем функцию spectrum из R.
I <- abs(fft(y))^2/240
P <- (4/240)*I[1:120]
f <- 0:119/240
plot(f[-1],P[-1], type="l", xlab="Frequency", ylab="Power")Мы очень ясно видим, что можем восстанавливать периодические сигналы, которые мы встроили в наш игрушечный временной ряд.
Несколько примеров
Корь
Grenfell et al. (2001) показывают поразительную периодичность кори в Великобритании в довакцинальную эру и то, как она затухает после внедрения безопасной и эффективной противокоревой вакцины.
Постройте исторические данные из Нью-Йорка, опубликованные Беном Болкером.
require(zoo)
meas <- read.table("https://web.stanford.edu/class/earthsys214/data/nycmeas.dat.txt", header=FALSE)
dimnames(meas)[[2]] <- c("Date","Cases")
meas1 <- zoo(meas$Cases, order.by=meas$Date)
plot(meas1, xlab="Date", ylab="Cases")Ряд выглядит крайне регулярно. Мы можем рассчитать его спектр мощности, чтобы определить, какие частоты преобладают в дисперсии. Спектр функции - это оболочка для вычисления периодограммы (т. е. оценки спектральной плотности) по временному ряду. Есть пара моментов, о которых следует помнить:
- Spectrum вычисляет частотную ось в количестве циклов на интервал выборки; имеет смысл преобразовывать в циклы в единицу времени (поэтому разделите на интервал выборки).
- Спектр будет гораздо более интерпретируемым, если он будет сглажен.
- Используйте аргумент spans, который указывает параметр (ы) для так называемого модифицированного ядра Даниэля для сглаживания спектра.
- Модифицированное ядро Даниэля - это, по сути, просто текущее среднее (см. код ниже, чтобы понять, что делают эти параметры).
- Нет четких правил, как это сделать (попробуйте несколько разных значений).
- Чем больше количество интервалов, тем больше сглаживания и тем ниже будут пики спектра.
- По умолчанию spectrum вычисляется спектр в логарифмической шкале.
- Используйте аргумент log = "no", чтобы изменить это значение по умолчанию.
- Спектр нужно умножить на 2, чтобы он фактически равнялся дисперсии.
# what is the spans argument doing?
# scalar argument
kernel("modified.daniell",2)## mDaniell(2)
## coef[-2] = 0.125
## coef[-1] = 0.250
## coef[ 0] = 0.250
## coef[ 1] = 0.250
## coef[ 2] = 0.125# vector argument
kernel("modified.daniell",c(1,1))## mDaniell(1,1)
## coef[-2] = 0.0625
## coef[-1] = 0.2500
## coef[ 0] = 0.3750
## coef[ 1] = 0.2500
## coef[ 2] = 0.0625mspect <- spectrum(meas$Cases, log="no", spans=c(2,2), plot=FALSE)
delta <- 1/12
specx <- mspect$freq/delta
specy <- 2*mspect$spec
plot(specx, specy, xlab="Period (years)", ylab="Spectral Density", type="l")Есть очень четкий пик в один год.
Пример денге
Cazellas et al. (2005): Значительная связь между Эль-Ниньо и заболеваемостью денге в Бангкоке и других частях Таиланда. Однако это сложно доказать. Бангкок показывает два режима заболеваемости: один годовой, а второй - 2-3-летний. Иногда 2-3-летний период является доминирующим в Бангкоке, но 2-3-летний период никогда не доминирует в остальной части Таиланда.
Считается, что периодичность (также наблюдаемая в Перу, Бангладеш и т. д.) обусловлена внутренней динамикой инфекции, то есть увеличением и уменьшением пула восприимчивых людей, подобно динамике (например) кори в Великобритании (Grenfell et al. 2001).
Мы можем использовать данные, предоставленные Проектом прогнозирования денге NOAA, для оценки спектральных характеристик случаев денге в Сан-Хуане, Пуэрто-Рико.
library(zoo)
dengue <- read.csv("https://web.stanford.edu/class/earthsys214/data/San_Juan_Training_Data.csv", header=TRUE)
tcases <- zoo(dengue$total_cases, as.Date(dengue$week_start_date))
plot(tcases, xlab="Date", ylab="Total Cases")## now all cases
acases <- zoo(dengue[,4:7],as.Date(dengue$week_start_date))
plot(acases, xlab="Date", ylab=list("Dengue 1","Dengue 2","Dengue 3","Dengue 4"), main="")- Спектр мощности для полных случаев
- Обрежьте первые 100 значений для построения графика, потому что спектр полностью выравнивается для промежутка более 3 лет.
dspect <- spectrum(dengue$total_cases, log="no", spans=c(5,5), plot=FALSE)
delta <- 7/365
specx <- dspect$freq/delta
specy <- 2*dspect$spec
plot(specx[1:100], specy[1:100], xlab="Period (years)", ylab="Spectral Density", type="l")Когерентность
Когерентность - это мера временного ряда, аналогичная корреляции. Это мера повторяющихся явлений (т. е. волн). Две волны когерентны, если они имеют постоянную относительную фазу.
Большинство подходов к поиску периодического поведения (включая когерентность) предполагают, что базовые ряды являются стационарными, что означает, что среднее значение процесса остается постоянным. Ясно, что это не очень хорошее предположение, когда целью анализа является изучение изменения окружающей среды. Вейвлеты позволяют нам изучать локализованное периодическое поведение. В частности, мы ищем области высокой мощности на графике частота-время.
Продемонстрируем это на игрушечном примере из пакета biwavelet. Мы знаем, что многомерный индекс ENSO (MEI) и круговорот северной части Тихого океана (NPGO) подвержены когерентным колебаниям с частотой примерно 5-12 лет. Небольшой набор данных включен в пакет biwavelet, который включает месячные значения этих двух рядов с 1950-2009 гг.
data("enviro.data")
head(enviro.data)## month year date mei npgo pdo
## 1 1 1950 1950-01-01 -1.052 -2.1883951 -2.13
## 2 2 1950 1950-02-01 -1.161 -1.4458314 -2.91
## 3 3 1950 1950-03-01 -1.285 -0.9650357 -1.13
## 4 4 1950 1950-04-01 -1.090 -0.8587880 -1.20
## 5 5 1950 1950-05-01 -1.434 -0.6340822 -2.23
## 6 6 1950 1950-06-01 -1.351 -0.5809843 -1.77mei <- with(enviro.data, cbind(date,mei))
npgo <- with(enviro.data, cbind(date,npgo))
## not run because it takes too long
## set nrands small to speed things up (default = 300)
## mg.wtc <- wtc(mei,npgo, nrands = 100)
## plot(mg.wtc, plot.cb=TRUE)Вейвлет-когерентность данных MEI и NPGO
Взаимосвязь Dengue 1 и Dengue 2 в Сан-Хуане?
Есть ли взаимосвязь между сероварами денге в Сан-Хуане, PR? Мы можем проверить согласованность временных рядов Dengue 1 и Dengue 2. Во-первых, проверьте функцию взаимной корреляции для рядов инфекций Dengue 1 и Dengue 2.
ccf(dengue$denv1_cases,dengue$denv2_cases, main="")Для коротких лагов явно существует значимая взаимная корреляция. Теперь мы можем исследовать вейвлет-когерентность двух рядов.
library(biwavelet)
## biwavelet requires input of nx2 matrices
len <- length(dengue$denv1_cases)
t1 <- cbind(dengue$week_start_date,dengue$denv1_cases)
t2 <- cbind(dengue$week_start_date,dengue$denv2_cases)
## don't want to actually do this because it takes a long time!
#d1d2.wtc <- wtc(t1,t2)
#plot(d1d2.wtc)Когерентность Dengue 1 и Dengue 2.
Похоже, что примерно за трехлетний период наблюдается некоторая значительная согласованность, особенно в начале 90-х годов, примерно в 2000 году, а затем в 2007-2008 годах.
Демонстрация того, как работают вейвлеты
Вейвлеты похожи на спектральный анализ, но они работают в разных масштабах. Предположим, у нас есть ряд x (t) x (t). Вейвлет-преобразование включает в себя умножение ряда на вейвлет, который был растянут до различных масштабов, охватывающих ряд, и суммирование этого произведения. Масштаб определяется параметром ττ. Обратите внимание, насколько это концептуально похоже на вычисление ковариации двух переменных.
library(biwavelet)
morlet <- function(x) exp(-x^2/2) * cos(5*x)
x <- seq(-4,4,length=1000)
y <- morlet(x)
plot(x,y,type="l", lwd=3, col="purple4",
ylim=c(-1.1,1.1),
xlab="",ylab=expression(psi[a,tau](t)))
abline(h=0, lwd=0.5, lty=3)Материнский вейвлет Морле
Теперь сгенерируйте периодический ряд и наложите на материнский вейвлет.
f <- expression(cos(2*pi*x)*exp(-pi*x^2))
plot(x,y,type="l", lwd=3, col="purple4",
ylim=c(-1.1,1.1),
xlab="",ylab=expression(psi[a,tau](t)))
abline(h=0, lwd=0.5, lty=3)
lines(x,eval(f), lwd=2)Мы видим, что вейвлет довольно хорошо улавливает это периодическое изменение. Вейвлет-преобразование сигнала (красный) показывает, что большая часть функции лежит выше линии x = 0, а ее сумма строго положительна.
dx <- diff(x)
dx <- c(dx,dx[999])
plot(x, y*eval(f)*dx, type="l", lwd=3, col="red", xlab="x",
ylab=expression(paste("integrand, ", psi[a,tau](t), x(t))))
abline(h=0, lty=2)Что происходит, если сигнал не соответствует вейвлету? На следующем рисунке сигнал, выделенный черным цветом, в значительной степени случаен по отношению к материнскому вейвлету. Когда мы строим вейвлет-преобразование этого сигнала (красный), есть примерно равная площадь над и под линией x = 0x = 0, а сумма фактически равна нулю.
# another function
f1 <- expression(cos(12*pi*x)*exp(-pi*x^2))
plot(x,y,type="l", lwd=3, col="purple4",
ylim=c(-1.1,1.1),
xlab="",ylab=expression(psi[a,tau](t)))
abline(h=0, lwd=0.5, lty=3)
lines(x,eval(f1), lwd=2)plot(x, y*eval(f1)*dx, type="l", lwd=3, col="red", xlab="x",
ylab=expression(paste("integrand, ", psi[a,tau](t), x(t))))
abline(h=0, lty=2)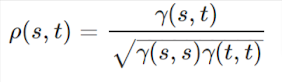


















Комментариев нет:
Отправить комментарий