В прошлой статье мы вместе увидели, как создать стохастический осциллятор с поправкой на волатильность. В этой статье мы будем использовать те же рассуждения о RSI, но мы будем делать поправку на корреляцию, а не на волатильность. Основная идея состоит в том, чтобы увидеть, хотим ли мы взвесить период ретроспективного анализа RSI на основе показателя скользящей корреляции.
Наш план будет заключаться в том, чтобы научиться кодировать RSI, который изменяет период ретроспективного анализа в каждый период времени на основе последней скользящей корреляции между ценой и моментумом. Причина, по которой я выбрал расчет моментума, заключается в том, что, мы еще не знаем период ретроспективного анализа для RSI, и, следовательно, мы не можем рассчитать меру корреляции специально для него. Когда мы знаем корреляцию между моментумом и рыночной ценой, мы можем преобразовать эту информацию в переменные периоды ретроспективного анализа для RSI. Мы увидим это более подробно ниже.
Индекс относительной силы (RSI)
Все мы знаем об индексе относительной силы - RSI и о том, как его использовать. Это, без сомнения, самый известный индикатор импульса, и этого следовало ожидать, поскольку у него много сильных сторон, особенно на при боковом движении рынка. Он также ограничен от 0 до 100, что упрощает его интерпретацию. Кроме того, тот факт, что он известен, увеличивает его потенциал.
Это связано с тем, что чем больше трейдеров и управляющих портфелем смотрят на RSI, тем больше людей будет реагировать на его сигналы, а это, в свою очередь, может подтолкнуть рыночные цены. Конечно, мы не можем доказать эту идею, но она интуитивно понятна, поскольку одна из основ технического анализа заключается в том, что она самореализируется.
Дж. Уэллс Уайлдер придумал этот индикатор в 1978 году как показатель импульса с оптимальным периодом ретроспективного анализа в 14 периодов. Он ограничен между 0 и 100, причем 30 и 70 являются согласованными зонами перепроданности и перекупленности соответственно. RSI можно использовать с помощью 4 известных методов:
- Зоны перепроданности/перекупленности как индикаторы краткосрочных коррекций.
- Отклонение от цены как признак истощения тренда.
- Нанесение на график индикатора графических линий для определения уровней реакции.
- Переход уровня нейтральности 50 как признак меняющейся динамики.
RSI рассчитывается довольно простым способом. Сначала мы берем разницу в ценах за один период. Это означает, что мы должны вычесть каждую цену закрытия из предыдущей. Затем мы вычислим сглаженное среднее положительных разностей и разделим его на сглаженное среднее отрицательных разностей. Последний расчет дает нам относительную силу, которая затем используется в формуле RSI для преобразования в меру от 0 до 100.
EURUSD и его 14-периодный RSI (изображение автора).
Сглаженная версия, используемая в расчетах Дж. Уэллса Уайлдера, связана с обычным экспоненциальным средним, к которому мы привыкли.
В приведенном ниже фрагменте кода показано, как рассчитать экспоненциальную скользящую среднюю и RSI. Я предоставил первую функцию, потому что она используется в формуле RSI в виде сглаженной скользящей средней. Вот пример:
def ema(Data, alpha, lookback, what, where):
# alpha is the smoothing factor
# window is the lookback period
# what is the column that needs to have its average calculated
# where is where to put the exponential moving average
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return Datadef rsi(Data, rsi_lookback, what1, what2):
rsi_lookback = (rsi_lookback * 2) - 1 # From exponential to smoothed
# Get the difference in price from previous step
delta = []
for i in range(len(Data)):
try:
diff = Data[i, what1] - Data[i - 1, what1]
delta = np.append(delta, diff)
except IndexError:
pass
delta = np.insert(delta, 0, 0, axis = 0)
delta = delta[1:]
# Make the positive gains (up) and negative gains (down) Series
up, down = delta.copy(), delta.copy()
up[up < 0] = 0
down[down > 0] = 0
up = np.array(up)
down = np.array(down)
roll_up = up
roll_down = down
roll_up = np.reshape(roll_up, (-1, 1))
roll_down = np.reshape(roll_down, (-1, 1))
roll_up = adder(roll_up, 3)
roll_down = adder(roll_down, 3)
roll_up = ema(roll_up, 2, rsi_lookback, what2, 1)
roll_down = ema(abs(roll_down), 2, rsi_lookback, what2, 1)
# Calculate the SMA
roll_up = roll_up[rsi_lookback:, 1:2]
roll_down = roll_down[rsi_lookback:, 1:2]
Data = Data[rsi_lookback + 1:,]
# Calculate the RSI based on SMA
RS = roll_up / roll_down
RSI = (100.0 - (100.0 / (1.0 + RS)))
RSI = np.array(RSI)
RSI = np.reshape(RSI, (-1, 1))
RSI = RSI[1:,]
Data = np.concatenate((Data, RSI), axis = 1)return Data
Сглаженная скользящая средняя за 200 периодов аналогична экспоненциальной скользящей средней за 399 периодов. Это означает, что для перехода от сглаженного к экспоненциальному среднему, мы можем умножить на два и вычесть единицу.
Однако в этой статье нас не интересует обычный RSI. Вместо этого мы рассчитаем скользящую 20-периодную корреляцию между показателем импульса и валютной парой, а затем определим для каждого периода оптимальный период ретроспективного анализа для RSI перед вычислением динамического RSI.
Следовательно, наша переменная (неизвестный элемент) в нашем уравнении будет периодом ретроспективного анализа. Мы попробуем найти интересный способ найти его, основываясь на силе корреляции моментума.
Итак, задача сводится к нахождению RSI, взвешенного по корреляции, на основе моментума цены. Описание сложнее, чем предмет на самом деле. Давайте начнем строить блок за блоком.
Создание динамического RSI
Первый шаг - вычислить моментум цены на основе последних 5 периодов. Это делается путем деления последней цены закрытия на цену закрытия 5 периодов назад:
Мы можем закодировать это с помощью этой функции:
def momentum_indicator(Data, what, where, lookback):
for i in range(len(Data)):
Data[i, where] = Data[i, what] / Data[i - lookback, what] * 100
return Data# The Data variable is the OHLC array
# The what variable is the closing price column
# The where variable is where to put the indicator
# The lookback variable is the subtraction range which is 5
Следующим шагом является вычисление 20-периодной скользящей корреляционной меры между ценой и расчетом импульса.
Корреляция - это степень линейной связи между двумя или более переменными. Она ограничена диапазоном от -1 до 1, причем один - это совершенная положительная корреляция, -1 - совершенная отрицательная корреляция, а 0 - показатель отсутствия линейной связи между переменными (они меняются в случайных направлениях относительно друг друга). Эта мера не идеальна и может быть подвержена смещению из-за выбросов и нелинейных зависимостей, однако она дает быстрый обзор статистических свойств. Наиболее распространенная мера корреляции называется корреляцией Пирсона, и мы будем использовать ее в этой статье.
from scipy.stats import pearsonrdef rolling_correlation(Data, first_data, second_data, lookback, where):
for i in range(len(Data)):
try:
Data[i, where] = pearsonr(Data[i - lookback + 1:i + 1, first_data], Data[i - lookback + 1:i + 1, second_data])[0]
except ValueError:
pass
Data = jump(Data, lookback)
return Data
EURUSD на первой панели, 5-периодный моментум на второй панели и их 20-периодная скользящая корреляция (изображение автора).
Последним шагом перед созданием динамического RSI является преобразование меры корреляции в переменные периоды ретроспективного анализа на каждом этапе во времени. Это означает, что мы заменим значения корреляции целыми числами на основе следующих условий:
- Всякий раз, когда корреляция между ценой и ее 5-периодным моментумом относительно высока в соответствии с последними 20 периодами, мы должны смещать период ретроспективного анализа RSI вниз, чтобы лучше учесть недавние значения.
- Всякий раз, когда корреляция между ценой и ее 5-периодным моментумом относительно низка в соответствии с последними 20 периодами, мы должны смещать период ретроспективного анализа RSI вверх, чтобы меньше учитывать недавние значения.
Мы можем использовать более сложные вещи для учета ретроспективных данных, но можем также попробовать что-нибудь чрезвычайно простое:
- Когда корреляция находится между -1,00 и 0,10, период ретроспективного анализа RSI равен 14.
- Когда корреляция находится между 0,10 и 0,20, период ретроспективного анализа RSI равен 10.
- Когда корреляция находится между 0,20 и 0,30, период ретроспективного анализа RSI равен 9.
- Когда корреляция составляет от 0,30 до 0,40, период ретроспективного анализа RSI равен 8.
- Когда корреляция находится между 0,40 и 0,50, период ретроспективного анализа RSI равен 7.
- Когда корреляция находится между 0,50 и 0,60, период ретроспективного анализа RSI равен 6.
- Когда корреляция находится между 0,60 и 0,70, период ретроспективного анализа RSI равен 5.
- Когда корреляция находится между 0,70 и 0,80, период ретроспективного анализа RSI равен 4.
- Когда корреляция находится между 0,80 и 0,90, период ретроспективного анализаRSI равен 3.
- Когда корреляция находится между 0,90 и 1,00, период ретроспективного анализа RSI равен 2.
Пример того, как ретроспективный анализ RSI изменяется с изменением корреляции (изображение автора).
Это способ постепенно взвешивать периоды ретроспективного анализа RSI. Обратите внимание, что вы можете выбрать любые периоды, которые хотите, и оптимизировать их в соответствии со своими предпочтениями. Параметры по умолчанию для Dynamic RSI (по моему мнению) такие же, как указано выше.
Давайте теперь посмотрим на полную функцию, которая выдает этот индикатор, прежде чем мы перейдем к этапу бэк-тестирования. Обратите внимание, что вы должны использовать его в массиве OHLC с несколькими дополнительными столбцами, которые будут заполнены функцией.
def dynamic_rsi(Data, momentum_lookback, corr_lookback, what, where):
for i in range(len(Data)):
Data[i, where] = Data[i, what] / Data[i - momentum_lookback, what] * 100Data = rolling_correlation(Data, what, where, corr_lookback, where + 1)
for i in range(len(Data)):
if Data[i, where + 1]>= -1.00 and Data[i, where + 1]<= 0.10:
Data[i, where + 1] = 14
if Data[i, where + 1] > 0.10 and Data[i, where + 1]<= 0.20:
Data[i, where + 1] = 10
if Data[i, where + 1] > 0.20 and Data[i, where + 1]<= 0.30:
Data[i, where + 1] = 9
if Data[i, where + 1] > 0.30 and Data[i, where + 1]<= 0.40:
Data[i, where + 1] = 8
if Data[i, where + 1] > 0.40 and Data[i, where + 1]<= 0.50:
Data[i, where + 1] = 7
if Data[i, where + 1] > 0.50 and Data[i, where + 1]<= 0.60:
Data[i, where + 1] = 6
if Data[i, where + 1] > 0.60 and Data[i, where + 1]<= 0.70:
Data[i, where + 1] = 5
if Data[i, where + 1] > 0.70 and Data[i, where + 1]<= 0.80:
Data[i, where + 1] = 4
if Data[i, where + 1] > 0.80 and Data[i, where + 1]<= 0.90:
Data[i, where + 1] = 3
if Data[i, where + 1] > 0.90 and Data[i, where + 1]<= 1.00:
Data[i, where + 1] = 2
Data = rsi(Data, 14, 3, 0)
Data = rsi(Data, 10, 3, 0)
Data = rsi(Data, 9, 3, 0)
Data = rsi(Data, 8, 3, 0)
Data = rsi(Data, 7, 3, 0)
Data = rsi(Data, 6, 3, 0)
Data = rsi(Data, 5, 3, 0)
Data = rsi(Data, 4, 3, 0)
Data = rsi(Data, 3, 3, 0)
Data = rsi(Data, 2, 3, 0)for i in range(len(Data)):
if Data[i, where + 1] == 14:
Data[i, where + 12] = Data[i, where + 2]
if Data[i, where + 1] == 10:
Data[i, where + 12] = Data[i, where + 3]
if Data[i, where + 1] == 9:
Data[i, where + 12] = Data[i, where + 4]
if Data[i, where + 1] == 8:
Data[i, where + 12] = Data[i, where + 5]
if Data[i, where + 1] == 7:
Data[i, where + 12] = Data[i, where + 6]
if Data[i, where + 1] == 6:
Data[i, where + 12] = Data[i, where + 7]
if Data[i, where + 1] == 5:
Data[i, where + 12] = Data[i, where + 8]
if Data[i, where + 1] == 4:
Data[i, where + 12] = Data[i, where + 9]
if Data[i, where + 1] == 3:
Data[i, where + 12] = Data[i, where + 10]
if Data[i, where + 1] == 2:
Data[i, where + 12] = Data[i, where + 11]return Data
Теперь, как результаты динамического RSI соотносятся с результатами обычного RSI? В конце концов, нам нужен эталон или какое-то сравнение, чтобы правильно судить о нашей стратегии. Я сделаю исключение в этом бэк-тесте в отношении применяемых мной процессов управления рисками, поскольку я буду соблюдать оптимальное соотношение риска и прибыли, равное 2,00. Это означает, что я буду размещать свои стопы на уровне 1x 50-периодного ATR, а мои цели - на 2x 50-периодном ATR. Это другой способ сказать, что я буду рисковать половиной того, что ожидаю получить в каждой сделке.
Иллюстрация почасовых данных AUDCAD в сравнении с динамическим RSI (изображение автора).
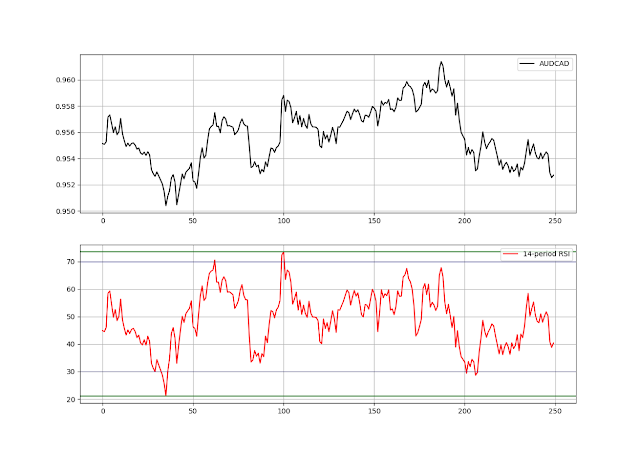
Иллюстрация часовых данных AUDCAD в сравнении с 14-периодным RSI (изображение автора).
На графиках ниже показаны таблицы результатов и кривые доходности стратегии, которая:
- Открывает длинную позицию (Buy), когда индикатор достигает 30, и удерживает позицию до тех пор, пока не будет сгенерирован новый сигнал или пока позиция не будет закрыта стоп-лоссом или тейк-профитом.
- Открывает короткую позицию (Sell), когда индикатор достигает 70, и удерживает позицию до тех пор, пока не будет сгенерирован новый сигнал или пока позиция не будет закрыта стоп-лоссом или тейк-профитом.
Сводная таблица эффективности (изображение автора).
Кривые капитала, соответствующие стратегии RSI слева, и стратегии динамического RSI справа (изображение автора).
Что впечатляет в Dynamic RSI, так это то, что он увеличивает прибыль, учитывая соотношение риска и вознаграждения 2,00. Он может снизить риск и увеличить доход. Чтобы узнать больше о корреляции на случай, если вам нужно освежить память, вы можете прочитать эту статью:
Лучше всего использовать динамический RSI (также известный как RSI, взвешенный по корреляции) в систематических стратегиях, потому что таким образом, мы можем оценить его эффективность за считанные минуты, также его можно использовать в дискреционной торговле с помощью тех же старых графических методов, описанных выше.
Становится интересным использовать динамический RSI, даже несмотря на то, что трейдеры более пристально следят за обычным RSI. Разница между ними, кажется, показывает, что у нас есть еще один индикатор. Может быть, однажды мы сможем объединить оба сигнала?
14-периодный RSI и динамический RSI на одном графике (изображение автора).
Заключение
Почему была написана эта статья? Это, конечно, не метод кормления с ложечки и не путь к прибыльной стратегии. Если вы будете следить за моими статьями, то заметите, что я больше акцентирую внимание на том, как это сделать, и что я также предоставляю функции, а не полный воспроизводимый код. В финансовой индустрии вам следует самостоятельно комбинировать кусочки другой информации и данных, только тогда вы овладеете искусством исследования и торговли.
Я всегда советую вам проводить надлежащие бэк-тесты и понимать любые риски, связанные с торговлей. Например, приведенные выше результаты не являются достоверными, поскольку использованный нами спред очень конкурентоспособен и может считаться труднодостижимым в мире реальной торговли (но не невозможным). Однако с помощью институциональных спредов спроса и предложения можно снизить затраты, например, если систематическая среднечастотная стратегия станет очень прибыльной. Вы никогда не должны ожидать гарантированной прибыли, и вы несете исключительную ответственность за генерирование собственных сигналов.










Комментариев нет:
Отправить комментарий