Известно, что две или более синусоидальных волн могут проходить один и тот же путь одновременно без взаимных помех. Для сложной волны, можно выделить ее компоненты (как это сделать - другая проблема).
xs <- seq(-2*pi,2*pi,pi/100)
wave.1 <- sin(3*xs)
wave.2 <- sin(10*xs)
par(mfrow = c(1, 2))
plot(xs,wave.1,type="l",ylim=c(-1,1)); abline(h=0,lty=3)
plot(xs,wave.2,type="l",ylim=c(-1,1)); abline(h=0,lty=3)которые можно линейно объединить в сложную волну:
wave.3 <- 0.5 * wave.1 + 0.25 * wave.2
plot(xs,wave.3,type="l"); title("Eg complex wave"); abline(h=0,lty=3)Ряды Фурье
Джозеф Фурье показал, что любую периодическую волну можно представить суммой простых синусоидальных волн. Эта сумма называется рядом Фурье. Ряд Фурье сохраняется только тогда, когда система линейна. Если есть, например, некоторый эффект переполнения (порог, при котором выходной сигнал остается неизменным независимо от ввода), в процесс входит нелинейный эффект, нарушающий синусоидальную волну и принцип суперпозиции.
wave.4 <- wave.3
wave.4[wave.3>0.5] <- 0.5
plot(xs,wave.4,type="l",ylim=c(-1.25,1.25)); title("overflowed, non-linear complex wave"); abline(h=0,lty=3)Кроме того, ряд Фурье имеет место только в том случае, если волны являются периодическими, т. е. имеют повторяющийся паттерн (непериодические волны обрабатываются преобразованием Фурье, см. ниже). Периодическая волна имеет частоту f и длину волны λ (длина волны - это расстояние в среде между началом и концом цикла, λ=v/fₒ, где v - скорость волны), которые определяются повторяющимся паттерном. Непериодическая волна не имеет частоты или длины волны.
Некоторые концепции:
- Основной период T - это период всех взятых отсчетов, время между первым и последним отсчетом.
- Частота дискретизации sr - это количество отсчетов, взятых за период времени (также называемая частотой сбора данных). Для простоты сделаем интервал времени между выборками равным. Этот временной интервал называется интервалом отсчетов, si, который представляет собой время основного периода, деленное на количество отсчетов N. Итак, si = T/N
- Основная частота fₒ, равная 1/T. Основная частота - это частота повторяющегося паттерна или длина волны. В предыдущих волнах основная частота составляла 1/2𝜋. Частоты волновых составляющих должны быть кратными основной частоте. fₒ называется первой гармоникой, вторая гармоника - 2 ∗ fₒ, третья - 3 ∗ fₒ и т. д.
repeat.xs <- seq(-2*pi,0,pi/100)
wave.3.repeat <- 0.5*sin(3*repeat.xs) + 0.25*sin(10*repeat.xs)
plot(xs,wave.3,type="l"); title("Repeating pattern")
points(repeat.xs,wave.3.repeat,type="l",col="red"); abline(h=0,v=c(-2*pi,0),lty=3)волна 3 - это взвешенная сумма волны 1 и волны 2. Это уравнение представляет собой ряд Фурье для волны 3:
f(t)=0.5×sin(3wt)+0.25×sin(10wt)
где w - угловая частота (также известная как угловая скорость) в радианах в секунду, w = 2𝜋fₒ, где fₒ - основная частота комплексной волны. В этом случае первая составляющая (волна 1) имеет в три раза большую частоту, а вторая составляющая в 10 раз больше частоты fₒ.
Вот функция R для построения траекторий с учетом ряда Фурье:
plot.fourier <- function(fourier.series, f.0, ts) {
w <- 2*pi*f.0
trajectory <- sapply(ts, function(t) fourier.series(t,w))
plot(ts, trajectory, type="l", xlab="time", ylab="f(t)"); abline(h=0,lty=3)
}
# An eg
plot.fourier(function(t,w) {sin(w*t)}, 1, ts=seq(0,1,1/100)) И построение уравнения
f(t)=0.5×sin(3wt)+0.25×sin(10wt):
acq.freq <- 100 # data acquisition frequency (Hz)
time <- 6 # measuring time interval (seconds)
ts <- seq(0,time,1/acq.freq) # vector of sampling time-points (s)
f.0 <- 1/time # fundamental frequency (Hz)
dc.component <- 0
component.freqs <- c(3,10) # frequency of signal components (Hz)
component.delay <- c(0,0) # delay of signal components (radians)
component.strength <- c(.5,.25) # strength of signal components
f <- function(t,w) {
dc.component +
sum( component.strength * sin(component.freqs*w*t + component.delay))
}
plot.fourier(f,f.0,ts) Фазовые сдвиги
Еще одна особенность ряда Фурье - фазовый сдвиг. Фазовые сдвиги - это сдвиги по оси x для заданного волнового компонента. Эти сдвиги измеряются в углах (радианах).
Взяв предыдущий пример и сдвинув волну 1 на 𝜋/2, мы получим следующий ряд Фурье:
f(t)=0.5×sin(3wt+𝜋/2)+0.25×sin(10wt)
который производит следующую траекторию:
component.delay <- c(pi/2,0) # delay of signal components (radians)
plot.fourier(f,f.0,ts)Компоненты DC
Эта концепция имеет дело с трансляциями по оси Y. Этому случаю соответствует аддитивный постоянный сигнал.
Применение компонента DC -2 к предыдущему результату приведет к следующему уравнению и графику:
f(t)=−2+0.5×sin(3wt+𝜋/2)+0.25×sin(10wt)
dc.component <- -2
plot.fourier(f,f.0,ts)Общее уравнение
Сложив эти понятия, мы получим общий вид ряда Фурье:
f(t)=aₒ + ∑aₖ × sin(kwt+ρₖ)
где aₒ - постоянная составляющая, w = 2𝜋fₒ, где fₒ - основная частота исходной волны.
Каждая волновая составляющая aₖ × sin(kwt+ρₖ) также называется гармоникой.
Существует также альтернативное представление с использованием тождества:
sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
которое позволяет заменять фазовые сдвиги косинусами.
Преобразование Фурье (FT) - это обобщение решения для непериодических волн. FT предполагает, что конечный анализируемый отрезок соответствует одному периоду бесконечно протяженного периодического сигнала.
Преобразование Фурье
Преобразование Фурье рассматривает каждую траекторию (или сигнал) как набор круговых движений.
Для данной траектории преобразование Фурье (FT) разбивает ее на набор связанных циклов, которые ее описывают. У каждого цикла есть сила, задержка и скорость. Эти циклы легче обрабатывать, т. е. сравнивать, изменять, упрощать, и при необходимости их можно использовать для восстановления исходной траектории.
Траектория обрабатывается через набор фильтров:
- каждый фильтр дает нам цикл и остаток траектории;
- фильтры независимы, каждый обрабатывает свою часть траектории;
- количество фильтров достаточно, чтобы обработать всю траекторию, т. е. последний фильтр не оставляет остатка траектории.
Результирующие циклы результатов можно комбинировать линейно, что дает одинаковые результаты независимо от порядка смешивания.
Таким образом, алгоритм FT получает траекторию, применяет свои фильтры для поиска подходящих циклов и выводит полный набор циклических компонентов. Есть два алгоритма:
- Дискретное преобразование Фурье (DFT), которое требует O(n2) операций (для n выборок).
- Быстрое преобразование Фурье (FFT), которое требует O(n.log (n)) операций.
В этом руководстве не рассматриваются алгоритмы. Есть функция R под названием fft(), которая вычисляет FFT.
Вот два примера использования: стационарная и возрастающая траектории:
library(stats)
fft(c(1,1,1,1)) / 4 # to normalize## [1] 1+0i 0+0i 0+0i 0+0ifft(1:4) / 4 ## [1] 2.5+0.0i -0.5+0.5i -0.5+0.0i -0.5-0.5iСкоро мы сможем интерпретировать эти результаты :-)
Сначала нам нужно резюмировать один конкретный математический момент.
Геометрическая интерпретация комплексных чисел
Приложение Geogebra, помогает объяснить, как мы можем интерпретировать геометрические выражения, такие как z×e^di. Пожалуйста, попробуйте поиграть с ним, пока не поймете.
Чтобы узнать об использовании комплексных чисел в R, посмотрите:
Свойства цикла
Мы упоминали, что у каждого цикла есть сила, задержка и скорость. Как мы можем их представить?
- Сила представлена размером круга, который контролируется z.
- Задержка или начальная точка задается начальным значением d.
- Скорость будет представлена скоростью изменения d с течением времени.
Вот анимация, беззастенчиво взятая из Better Explained, описывающая круговой путь:
Во всяком случае, помните этот вывод?
fft(1:4) / 4 # to normalize## [1] 2.5+0.0i -0.5+0.5i -0.5+0.0i -0.5-0.5iВот анимация той же траектории:
Анимацию можно посмотреть по следующей ссылке:
В текстовом поле Cycles значения после двоеточия означают начальную точку этого цикла (в градусах), то есть задержку цикла. Итак: 180 означает, что цикл начинается с начального поворота на 180 градусов или 𝜋 радиан.
Циклы, показанные здесь для траектории 1,2,3,4, равны 2,5 0,71: 135 0,5: 180 0,71: -135, что является еще одним способом представления выходных данных функции fft() R. Функция fft() возвращает последовательность комплексных чисел, а анимация возвращает пары сила: задержка (в градусах).
Вот небольшая функция для преобразования вывода fft() в вывод анимации:
# cs is the vector of complex points to convert
convert.fft <- function(cs, sample.rate=1) {
cs <- cs / length(cs) # normalize
distance.center <- function(c)signif( Mod(c), 4)
angle <- function(c)signif( 180*Arg(c)/pi, 3)
df <- data.frame(cycle = 0:(length(cs)-1),
freq = 0:(length(cs)-1) * sample.rate / length(cs),
strength = sapply(cs, distance.center),
delay = sapply(cs, angle))
df
}
convert.fft(fft(1:4))## cycle freq strength delay
## 1 0 0.00 2.5000 0
## 2 1 0.25 0.7071 135
## 3 2 0.50 0.5000 180
## 4 3 0.75 0.7071 -13который является результатом предыдущей анимации.
Так что она заботится о силе и задержке. А как насчет скорости? Это дается последовательностью циклов. Первый цикл является стационарным (0 Гц, т. е. составляющая постоянного тока), затем для каждого следующего цикла частота увеличивается (1 Гц, 2 Гц, 3 Гц,…).
Попробуйте эти последовательности циклов в анимации:
1
0 1 это первая анимация
0 0 1
и так далее, пока вы не поймете закономерность ...
Последовательность циклов с одной единицей в i-й позиции означает чистый цикл (i + 1) Гц, т. е. он выполняет i + 1 цикл за интервал времени.
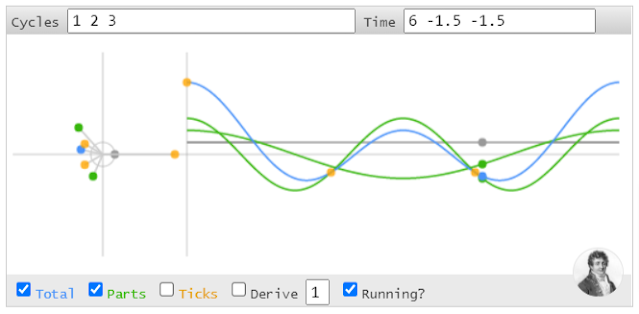
Также можно комбинировать их! Последовательность 1 2 3 означает, что цикл 0 Гц имеет силу 1, цикл 1 Гц имеет силу 2, а цикл 2 Гц имеет силу 3:
Ссылка на анимацию:
Видите, как самый большой зеленый вектор слева вращается быстрее? Это цикл 2 Гц, которому мы дали наибольшую силу.
Желтые точки (или галочки) означают равные промежутки времени до повторения траектории. В данном случае их 3, так как у нас есть периоды до 2 Гц. При отметке 0 три цикла имеют общую силу 6 (1 + 2 + 3), поскольку все они начинаются под нулевым углом (без задержек). На тике 1 их сумма равна -1,5, поскольку и 2-й, и 3-й цикл вносят отрицательный вклад, что снова происходит на тике 2. После этого траектория возобновляется.
Синяя линия - это взвешенная сумма значений всех циклов. Обратите внимание, что синяя линия также имеет значения между точками данных. Считайте это интерполяцией, значения, которые предлагает это моделирование, где сигнал должен быть между двумя заданными точками данных. Но важно то, что в требуемых точках функция имеет правильные значения.
С набором циклов 1 2 3: 180 мы видим, что изначально цикл 2 Гц начинается с противоположной стороны, и поэтому объединенная сила первых двух циклов уравновешивает в точности силу третьего цикла. Вот почему первый номер траектории равен нулю.
Обычно мы хотим знать обратное: какими должны быть циклы, чтобы их совокупные силы приводили к заданной известной траектории? Это то, что вычисляет DFT/FFT.
Скажем, нам нужны значения 4 0 0 0 во временном ряду (пик каждые четыре единицы времени). У нас должны быть циклы, которые сначала начинаются с суммы 4, а затем отменяют друг друга для следующих 3 временных шагов. Используйте анимацию, чтобы узнать, что это за циклы. Решение: 1 1 1 1. То есть сначала все четыре цикла вносят вклад в выходной сигнал, затем в момент времени t = 1 цикл 2 Гц отменяет цикл 0 Гц (компонент постоянного тока), в то время как 1 Гц и 3 Гц равны нулю. Для времени t = 2 смотрите сами, какие циклы гасят друг друга. В течение последних трех моментов существует деструктивная интерференция между всеми четырьмя циклами (от 0 Гц до 3 Гц).
Уравнения
Преобразование Фурье преобразует волну из временной области в частотную. Существует набор синусоид, которые в сумме равны любой данной волне. Каждая из этих синусоидальных волн имеет свою частоту и амплитуду. График зависимости частоты от силы (амплитуды) на графике x-y этих составляющих синусоидальной волны представляет собой частотный спектр (мы увидим его вкратце), т.е. траекторию можно перевести в набор частотных всплесков.
В терминах уравнений:
где:
Xₖ - величина частоты k в сигнале; каждое значение k^th представляет собой комплексное число, включающее силу (амплитуду) и фазовый сдвиг.
N - количество образцов.
n - текущая выборка, n∈ {0… N − 1}
k - частота, от 0 Гц до N-1 Гц
1/N не требуется, но дает фактические размеры временных пиков.
n/N - это процент времени, которое мы прошли.
2𝜋k - скорость в радианах в секунду.
e^(−ix): круговое движение в обратном направлении. Последние три значения показывают, как далеко мы продвинулись при этой скорости за это время.
Функция fft() возвращает эти Xₖ.
Обратное преобразование Фурье (IFT) преобразует компоненты частотной области обратно в исходную временную волну. Она задается следующим уравнением:
Функция, которая возвращает интерполированную траекторию с учетом Xₖ. Она интерполируется, потому что единственные известные нам данные - это измерения (например, некоторые точки, такие как (t = 0, signal = 4), (1,0), (2,0) и (3,0)). Все остальное дается результатами из ряда Фурье, вычисленного функцией fft().
Для выполнения IFT используйте fft(X.k, inverse = TRUE)/length (X.k).
В любом случае, вот функция, которая применяет предыдущее уравнение, то есть делает IFT:
# returns the x.n time series for a given time sequence (ts) and
# a vector with the amount of frequencies k in the signal (X.k)
get.trajectory <- function(X.k,ts,acq.freq) {
N <- length(ts)
i <- complex(real = 0, imaginary = 1)
x.n <- rep(0,N) # create vector to keep the trajectory
ks <- 0:(length(X.k)-1)
for(n in 0:(N-1)) { # compute each time point x_n based on freqs X.k
x.n[n+1] <- sum(X.k * exp(i*2*pi*ks*n/N)) / N
}
x.n * acq.freq
}Вот две полезные функции:
plot.frequency.spectrum() строит спектр частого для заданной Xₖ.
plot.harmonic() отображает i-ю гармонику на текущем графике.
plot.frequency.spectrum <- function(X.k, xlimits=c(0,length(X.k))) {
plot.data <- cbind(0:(length(X.k)-1), Mod(X.k))
# TODO: why this scaling is necessary?
plot.data[2:length(X.k),2] <- 2*plot.data[2:length(X.k),2]
plot(plot.data, t="h", lwd=2, main="",
xlab="Frequency (Hz)", ylab="Strength",
xlim=xlimits, ylim=c(0,max(Mod(plot.data[,2]))))
}
# Plot the i-th harmonic
# Xk: the frequencies computed by the FFt
# i: which harmonic
# ts: the sampling time points
# acq.freq: the acquisition rate
plot.harmonic <- function(Xk, i, ts, acq.freq, color="red") {
Xk.h <- rep(0,length(Xk))
Xk.h[i+1] <- Xk[i+1] # i-th harmonic
harmonic.trajectory <- get.trajectory(Xk.h, ts, acq.freq=acq.freq)
points(ts, harmonic.trajectory, type="l", col=color)
}Давайте проверим, например, последнюю. Обратите внимание, что этот график совпадает с синей линией в анимации:
X.k <- fft(c(4,0,0,0)) # get amount of each frequency k
time <- 4 # measuring time interval (seconds)
acq.freq <- 100 # data acquisition frequency (Hz)
ts <- seq(0,time-1/acq.freq,1/acq.freq) # vector of sampling time-points (s)
x.n <- get.trajectory(X.k,ts,acq.freq) # create time wave
plot(ts,x.n,type="l",ylim=c(-2,4),lwd=2)
abline(v=0:time,h=-2:4,lty=3); abline(h=0)
plot.harmonic(X.k,1,ts,acq.freq,"red")
plot.harmonic(X.k,2,ts,acq.freq,"green")
plot.harmonic(X.k,3,ts,acq.freq,"blue")В результате получаем много гармоник. Некоторые из них, возможно, являются результатом шума и, надеюсь, будут очень слабыми. Обычно нам нужны только сильные гармоники: те, которые вносят значительный вклад в сигнал.
Наивысшая значимая частота синусоидальной волны (после fft-анализа формы исходного сигнала) находится на половине частоты сбора данных, потому что наш входной сигнал состоит из реальных значений (т. е. траектория не имеет мнимых частей). Последняя полезная точка находится по адресу acq.freq/2. Частота Найквиста составляет половину частоты дискретизации. Частота Найквиста - это максимальная частота, которая может быть обнаружена для данной частоты дискретизации. Это связано с тем, что для измерения волны вам понадобится по крайней мере одна впадина и один пик, чтобы идентифицировать ее.
Важным моментом является то, что любой сигнал можно описать двумя способами:
- во временной области, ось x - это временная переменная, а ось y - амплитуда сигнала.
- в частотной области, ось x - это частотная переменная, а ось y - амплитуда сигнала.
Иногда легче работать с одним описанием, иногда - с другим.
DFT и IFT - это математические инструменты, которые переводят эти два описания друг в друга.
Примеры
Давай построим траекторию по следующей сложной волне
f(t)=2+0.75×sin(3wt)+0.25×sin(7wt)+0.5×sin(10wt)
acq.freq <- 100 # data acquisition (sample) frequency (Hz)
time <- 6 # measuring time interval (seconds)
ts <- seq(0,time-1/acq.freq,1/acq.freq) # vector of sampling time-points (s)
f.0 <- 1/time
dc.component <- 1
component.freqs <- c(3,7,10) # frequency of signal components (Hz)
component.delay <- c(0,0,0) # delay of signal components (radians)
component.strength <- c(1.5,.5,.75) # strength of signal components
f <- function(t,w) {
dc.component +
sum( component.strength * sin(component.freqs*w*t + component.delay))
}
plot.fourier(f,f.0,ts=ts)Предположим, мы не знаем функциональную форму траектории, у нас есть только ее содержание, период и моменты времени выборки:
w <- 2*pi*f.0
trajectory <- sapply(ts, function(t) f(t,w))
head(trajectory,n=30)## [1] 1.000000 1.162132 1.323161 1.481997 1.637568 1.788836 1.934801
## [8] 2.074515 2.207089 2.331703 2.447610 2.554146 2.650736 2.736896
## [15] 2.812242 2.876489 2.929454 2.971057 3.001324 3.020382 3.028458
## [22] 3.025877 3.013056 2.990502 2.958803 2.918623 2.870694 2.815807
## [29] 2.754805 2.688575Итак, учитывая эту траекторию, мы можем найти, где находятся пики частоты:
X.k <- fft(trajectory) # find all harmonics with fft()
plot.frequency.spectrum(X.k, xlimits=c(0,20))И если бы у нас были только пики частоты, мы могли бы восстановить сигнал:
x.n <- get.trajectory(X.k,ts,acq.freq) / acq.freq # TODO: why the scaling?
plot(ts,x.n, type="l"); abline(h=0,lty=3)
points(ts,trajectory,col="red",type="l") # compare with originalЭта функция предназначена только для презентационных целей:
plot.show <- function(trajectory, time=1, harmonics=-1, plot.freq=FALSE) {
acq.freq <- length(trajectory)/time # data acquisition frequency (Hz)
ts <- seq(0,time-1/acq.freq,1/acq.freq) # vector of sampling time-points (s)
X.k <- fft(trajectory)
x.n <- get.trajectory(X.k,ts, acq.freq=acq.freq) / acq.freq
if (plot.freq)
plot.frequency.spectrum(X.k)
max.y <- ceiling(1.5*max(Mod(x.n)))
if (harmonics[1]==-1) {
min.y <- floor(min(Mod(x.n)))-1
} else {
min.y <- ceiling(-1.5*max(Mod(x.n)))
}
plot(ts,x.n, type="l",ylim=c(min.y,max.y))
abline(h=min.y:max.y,v=0:time,lty=3)
points(ts,trajectory,pch=19,col="red") # the data points we know
if (harmonics[1]>-1) {
for(i in 0:length(harmonics)) {
plot.harmonic(X.k, harmonics[i], ts, acq.freq, color=i+1)
}
}
}Убывающий сигнал:
trajectory <- 4:1
plot.show(trajectory, time=2)Ступенчатый сигнал:
trajectory <- c(rep(1,5),rep(2,6),rep(3,7))
plot.show(trajectory, time=2, harmonics=0:3, plot.freq=TRUE)Качели:
trajectory <- c(1:5,2:6,3:7)
plot.show(trajectory, time=1, harmonics=c(1,2))Предположим, что этот временной ряд с сильным шумовым компонентом:
set.seed(101)
acq.freq <- 200
time <- 1
w <- 2*pi/time
ts <- seq(0,time,1/acq.freq)
trajectory <- 3*rnorm(101) + 3*sin(3*w*ts)
plot(trajectory, type="l")Мы можем проверить, не скрыта ли в нем какая-то гармоника (есть одна гармоника 3 Гц):
X.k <- fft(trajectory)
plot.frequency.spectrum(X.k,xlimits=c(0,acq.freq/2))И, как и ожидалось, мы находим пик на гармониках 3 Гц!
Есть несколько библиотек R (сюрприз!), которые создают этот тип частотных графиков. Вот один пример (результаты не совсем совпадают, что может быть следствием немного разных алгоритмов…):
library(GeneCycle)
f.data <- GeneCycle::periodogram(trajectory)
harmonics <- 1:(acq.freq/2)
plot(f.data$freq[harmonics]*length(trajectory),
f.data$spec[harmonics]/sum(f.data$spec),
xlab="Harmonics (Hz)", ylab="Amplitute Density", type="h")Также проверьте stats::Spectrum() и TSA::periodogram().
Если во временном ряду есть тренд, его следует исключить.
Например:
trajectory1 <- trajectory + 25*ts # let's create a linear trend
plot(trajectory1, type="l")f.data <- GeneCycle::periodogram(trajectory1)
harmonics <- 1:20
plot(f.data$freq[harmonics]*length(trajectory1),
f.data$spec[harmonics]/sum(f.data$spec),
xlab="Harmonics (Hz)", ylab="Amplitute Density", type="h")Временные ряды с трендом не зафиксировали сигнал.
Давайте удалим тренд, то есть найдем линейный тренд и поработаем с остатками:
trend <- lm(trajectory1 ~ts)
detrended.trajectory <- trend$residuals
plot(detrended.trajectory, type="l")f.data <- GeneCycle::periodogram(detrended.trajectory)
harmonics <- 1:20
plot(f.data$freq[harmonics]*length(detrended.trajectory),
f.data$spec[harmonics]/sum(f.data$spec),
xlab="Harmonics (Hz)", ylab="Amplitute Density", type="h")Теперь сигнал был пойман!
Кроме того, если мы пытаемся идентифицировать сигналы частот n × F Гц, длина временного ряда должна делиться на F, т.е. мы должны сделать что-то вроде detrended.trajectory [- (1: (length (detrended.trajectory) %% F))].
Давайте попробуем использовать настоящий набор данных, загруженный из Quandl, по розничным ценам на бензин с 1995 года по настоящее время.
library(zoo) # use: index() converts Date to its index ##
## Attaching package: 'zoo'
##
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numericprices <- read.csv("retailgas.csv") # weekly prices (1 Hz = 1 Week)
prices <- prices[order(nrow(prices):1),] # revert data frame
plot(prices, type="l")
trend <- lm(Price ~ index(Date), data = prices)
abline(trend, col="red")detrended.trajectory <- trend$residuals
plot(detrended.trajectory, type="l", main="detrended time series")f.data <- GeneCycle::periodogram(detrended.trajectory)
harmonics <- 1:20
plot(f.data$freq[harmonics]*length(detrended.trajectory),
f.data$spec[harmonics]/sum(f.data$spec),
xlab="Harmonics (Hz)", ylab="Amplitute Density", type="h")И мы можем видеть, что более сильные сигналы - это 1 Гц, 2 Гц и 3 Гц, что имеет определенный смысл. Заработная плата имеет месячный или двухнедельный цикл, который отражается на первых гармониках (1 Гц здесь соответствует 1 недельному циклу, 2 Гц означает каждые 2 недели и т. д.).
Оригинал: Fourier Transform: A R Tutorial






























Комментариев нет:
Отправить комментарий