Введение в прогнозирование временных рядов с помощью torch

Этот пост представляет собой введение в прогнозирование временных рядов с помощью torch. Центральными темами являются ввод данных и практическое использование RNN (GRU/LSTM). Следующие публикации будут основаны на этой и представят все более сложные архитектуры.

Это первая публикация из серии, посвященной прогнозированию временных рядов с помощью torch. Она требует некоторого предыдущего опыта работы с Torch и/или глубоким обучением. Но что касается временных рядов, то они рассматриваются с самого начала, используя рекуррентные нейронные сети (GRU или LSTM), чтобы предсказать, как что-то будет развиваться во времени.

В этом посте мы создаем сеть, которая использует последовательность наблюдений для прогнозирования значения на следующий момент времени. Что, если мы хотим спрогнозировать последовательность значений, соответствующую, скажем, неделе или месяцу измерений?

Также мы могли бы вернуть в систему ранее спрогнозированное значение, мы попробуем это в конце этой публикации. В следующих статьях будут рассмотрены другие варианты, некоторые из которых предполагают значительно более сложные архитектуры. Будет интересно сравнить их; но основная цель состоит в том, чтобы представить несколько «рецептов» torch, которые вы можете применить к своим собственным данным.

Начнем с изучения используемого набора данных. Он низкоразмерный, но довольно поливалентный и сложный.

Проверка временных рядов

Набор данных vic_elec, доступный через пакет tsibbledata, содержит получасовую потребность в электроэнергии за три года для Виктории, Австралия, и дополнен информацией о температуре с таким же разрешением и индикатором выходных.

library(tidyverse)
library(lubridate)

library(tsibble) # Tidy Temporal Data Frames and Tools
library(feasts) # Feature Extraction and Statistics for Time Series
library(tsibbledata) # Diverse Datasets for 'tsibble'

vic_elec %>% glimpse()

Rows: 52,608
Columns: 5
$ Time        <dttm> 2012-01-01 00:00:00, 2012-01-01 00:30:00, 2012-01-01 01:00:00,…
$ Demand      <dbl> 4382.825, 4263.366, 4048.966, 3877.563, 4036.230, 3865.597, 369…
$ Temperature <dbl> 21.40, 21.05, 20.70, 20.55, 20.40, 20.25, 20.10, 19.60, 19.10, …
$ Date        <date> 2012-01-01, 2012-01-01, 2012-01-01, 2012-01-01, 2012-01-01, 20…
$ Holiday     <lgl> TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRU…

В зависимости от того, какое подмножество переменных используется, а также от того, агрегируются ли данные во времени и как, эти данные могут служить для иллюстрации множества различных методов. Например, в третьем издании книги «Forecasting: Principles and Practice» ежедневные средние значения используются для обучения квадратичной регрессии с ошибками ARMA. Однако в этом первом вводном посте, как и в большинстве последующих, мы попытаемся спрогнозировать потребность, не полагаясь на дополнительную информацию, и сохраним исходное решение.

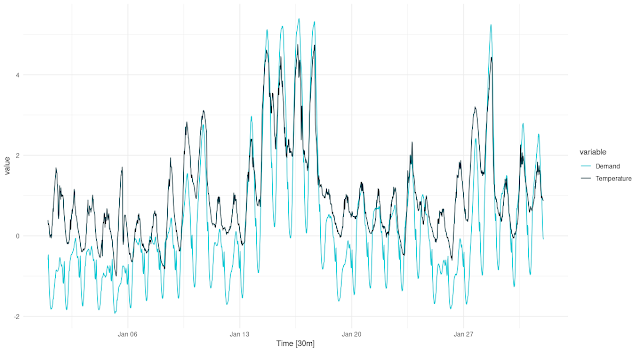
Чтобы получить представление о том, как спрос на электроэнергию меняется в разных временных масштабах, давайте рассмотрим данные за два месяца, которые хорошо иллюстрируют U-образную зависимость между температурой и спросом: январь 2014 г. и июль 2014 г.

Во-первых, июль.

vic_elec_2014 <-  vic_elec %>%
  filter(year(Date) == 2014) %>%
  select(-c(Date, Holiday)) %>%
  mutate(Demand = scale(Demand), Temperature = scale(Temperature)) %>%
  pivot_longer(-Time, names_to = "variable") %>%
  update_tsibble(key = variable)

vic_elec_2014 %>% filter(month(Time) == 7) %>% 
  autoplot() + 
  scale_colour_manual(values = c("#08c5d1", "#00353f")) +
  theme_minimal()

Рисунок 1: Температура и потребность в электроэнергии (нормализованные). Виктория, Австралия, 07/2014.

Сейчас зима, температура колеблется ниже среднего, а потребность в электроэнергии выше среднего (отопление). В течение дня наблюдаются сильные колебания, мы видим впадины на кривой спроса, соответствующие выступам на графике температуры, и наоборот. Хотя преобладают суточные колебания, существуют также колебания по дням недели. Однако между неделями мы не видим большой разницы.

Сравните это с данными за январь:

vic_elec_2014 %>% filter(month(Time) == 1) %>% 
  autoplot() + 
  scale_colour_manual(values = c("#08c5d1", "#00353f")) +
  theme_minimal()

Рисунок 2: Температура и потребность в электроэнергии (нормализованные). Виктория, Австралия, 01/2014.

Мы по-прежнему наблюдаем сильные циркадные колебания. Мы все еще наблюдаем некоторые колебания по дням недели. Но сейчас именно высокие температуры вызывают повышенный спрос (охлаждение). Также есть два периода необычно высоких температур, сопровождаемых исключительным спросом. Мы ожидаем, что в однофакторном прогнозе, без учета температуры, это будет трудно, или даже невозможно спрогнозировать.

Давайте посмотрим вкратце, как ведет себя Demand, используя feasts::STL(). Во-первых, вот разложение на июль:

vic_elec_2014 <-  vic_elec %>%
  filter(year(Date) == 2014) %>%
  select(-c(Date, Holiday))

cmp <- vic_elec_2014 %>% filter(month(Time) == 7) %>%
  model(STL(Demand)) %>% 
  components()

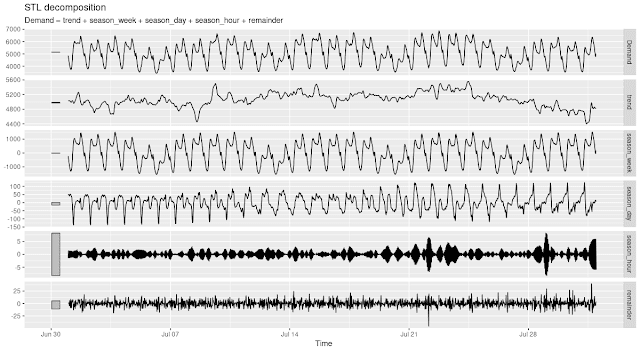
cmp %>% autoplot()

Рисунок 3: STL-декомпозиция спроса на электроэнергию. Виктория, Австралия, 07/2014.

А вот на январь:

Рисунок 4: STL-декомпозиция спроса на электроэнергию. Виктория, Австралия, 01/2014.

Оба прекрасно иллюстрируют сильные суточные и недельные сезонные колебания (при этом суточные колебания значительно сильнее в январе). Если мы присмотримся, мы даже увидим, что трендовый компонент более влиятельный в январе, чем в июле. Это снова намекает на гораздо более сильные трудности с предсказанием развития событий в январе, чем в июле.

Теперь, когда у нас есть представление о том, что нас ждет, давайте начнем с создания набора данных torch.

Ввод данных

Вот что мы собираемся делать. Мы хотим начать наше путешествие в области прогнозирования с использования последовательности наблюдений для прогнозирования их ближайшего значения. Другими словами, вход (x) для каждого элемента пакета - это вектор, а цель (y) - одно значение. Длина входной последовательности x параметризуется как n_timesteps, количество последовательных наблюдений, из которых следует экстраполировать цель.

Набор данных отразит это в своем методе .getitem(). При запросе наблюдений с индексом i он вернет тензоры следующим образом:

list(
      x = self$x[start:end],
      y = self$x[end+1]
)

где start:end - это вектор индексов длиной n_timesteps, а end + 1 - единственный индекс.

Теперь, если dataset просто итерировал входные данные по порядку, наращивая индекс по единице, эти строки могли бы просто читать

list(
      x = self$x[i:(i + self$n_timesteps - 1)],
      y = self$x[self$n_timesteps + i]
)

Поскольку многие последовательности в данных похожи, мы можем сократить время обучения, используя часть данных в каждую эпоху. Это может быть выполнено (необязательно) передачей значения sample_frac меньше 1. В initialize() подготавливается случайный набор начальных индексов; .getitem() тогда просто делает то, что обычно делает: ищет пару (x, y) по заданному индексу.

Вот полный код dataset:

elec_dataset <- dataset(
  name = "elec_dataset",
  
  initialize = function(x, n_timesteps, sample_frac = 1) {

    self$n_timesteps <- n_timesteps
    self$x <- torch_tensor((x - train_mean) / train_sd)
    
    n <- length(self$x) - self$n_timesteps 
    
    self$starts <- sort(sample.int(
      n = n,
      size = n * sample_frac
    ))

  },
  
  .getitem = function(i) {
    
    start <- self$starts[i]
    end <- start + self$n_timesteps - 1
    
    list(
      x = self$x[start:end],
      y = self$x[end + 1]
    )

  },
  
  .length = function() {
    length(self$starts) 
  }
)

Вы могли заметить, что мы нормализуем данные с помощью глобально определенных train_mean и train_sd. Нам еще предстоит их вычислить.

Мы разделяем данные очень просто. Мы используем весь 2012 год для обучения и весь 2013 год для проверки. Для тестирования мы возьмем «сложный» месяц январь 2014 года. Вам предлагается сравнить результаты тестирования за июль того же года и сравнить характеристики.

vic_elec_get_year <- function(year, month = NULL) {
  vic_elec %>%
    filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else 

month) %>%
    as_tibble() %>%
    select(Demand)
}

elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix() # or 2014, 7, alternatively

train_mean <- mean(elec_train)
train_sd <- sd(elec_train)

Теперь, чтобы создать экземпляр набора данных, нам все еще нужно выбрать длину последовательности. Судя по предварительному осмотру, неделя кажется разумным выбором.

n_timesteps <- 7 * 24 * 2 # days * hours * half-hours

Теперь мы можем продолжить и создать набор данных для обучающих данных. Допустим, мы будем использовать 50% данных за каждую эпоху:

train_ds <- elec_dataset(elec_train, n_timesteps, sample_frac = 0.5)
length(train_ds)

8615

Быстрая проверка: правильные ли формы данных?

train_ds[1]

$x
torch_tensor
-0.4141
-0.5541
[...]       ### lines removed by me
 0.8204
 0.9399
... [the output was truncated (use n=-1 to disable)]
[ CPUFloatType{336,1} ]

$y
torch_tensor
-0.6771
[ CPUFloatType{1} ]

Да: это то, что мы хотели увидеть. Входная последовательность имеет n_timesteps значений в первом измерении и одно значение во втором, что соответствует единственному присутствующему признаку, Demand. Как и предполагалось, тензор прогноза содержит единственное значение, соответствующее, как мы знаем, n_timesteps + 1.

Это касается одной пары ввода-вывода. Как обычно, пакетирование осуществляется классом dataloader из torch. Мы создаем экземпляр для обучающих данных и сразу же снова проверяем результат:

batch_size <- 32
train_dl <- train_ds %>% dataloader(batch_size = batch_size, shuffle = TRUE)
length(train_dl)

b <- train_dl %>% dataloader_make_iter() %>% dataloader_next()
b

$x
torch_tensor
(1,.,.) = 
  0.4805
  0.3125
[...]       ### lines removed by me
 -1.1756
 -0.9981
... [the output was truncated (use n=-1 to disable)]
[ CPUFloatType{32,336,1} ]

$y
torch_tensor
 0.1890
 0.5405
[...]       ### lines removed by me
 2.4015
 0.7891
... [the output was truncated (use n=-1 to disable)]
[ CPUFloatType{32,1} ]

Мы видим добавленную размерность batch впереди, в результате чего получается общая форма (batch_size, n_timesteps, num_features). Это формат, ожидаемый моделью, или, точнее, начальным слоем RNN.

Прежде чем мы продолжим, давайте быстро создадим наборы данных и загрузчики данных для проверки и тестирования данных.

valid_ds <- elec_dataset(elec_valid, n_timesteps, sample_frac = 0.5)
valid_dl <- valid_ds %>% dataloader(batch_size = batch_size)

test_ds <- elec_dataset(elec_test, n_timesteps)
test_dl <- test_ds %>% dataloader(batch_size = 1)

Модель

Модель состоит из RNN типа GRU или LSTM, по выбору пользователя, и выходного уровня. RNN выполняет большую часть работы; линейный слой с одним нейроном, который выводит прогноз, сжимает свой векторный вход до единственного значения.

Здесь, во-первых, определение модели.

model <- nn_module(
  
  initialize = function(type, input_size, hidden_size, num_layers = 1, dropout = 0) {
    
    self$type <- type
    self$num_layers <- num_layers
    
    self$rnn <- if (self$type == "gru") {
      nn_gru(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        dropout = dropout,
        batch_first = TRUE
      )
    } else {
      nn_lstm(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        dropout = dropout,
        batch_first = TRUE
      )
    }
    
    self$output <- nn_linear(hidden_size, 1)
    
  },
  
  forward = function(x) {
    
    # list of [output, hidden]
    # we use the output, which is of size (batch_size, n_timesteps, hidden_size)
    x <- self$rnn(x)[[1]]
    
    # from the output, we only want the final timestep
    # shape now is (batch_size, hidden_size)
    x <- x[ , dim(x)[2], ]
    
    # feed this to a single output neuron
    # final shape then is (batch_size, 1)
    x %>% self$output() 
  }
  
)

Самое главное, это то, что происходит в forward().

1. RNN возвращает список. Список содержит два тензора, выход и синопсис скрытых состояний. Мы отбрасываем тензор состояний и оставляем только вывод. Различие между состоянием и выходом, или, скорее, то, как оно отражается в том, что возвращает torch RNN, заслуживает более внимательного изучения. Мы сделаем это через секунду.

x <- self$rnn(x)[[1]]

2. Однако из выходного тензора нас интересует только последний временной шаг.

x <- x[ , dim(x)[2], ]

3. Только этот, таким образом, передается на выходной слой.

x %>% self$output()

4. Наконец, возвращается результат указанного выходного слоя.

Теперь немного подробнее о состояниях и выходах. Рассмотрим рис. 1 из Goodfellow, Bengio и Courville (2016).

Рисунок 5: Источник: Гудфеллоу и др., Глубокое обучение. URL-адрес главы: https://www.deeplearningbook.org/contents/rnn.html.

Представим, что есть только три временных шага, соответствующие t − 1, t и t + 1. Входная последовательность, соответственно, состоит из xt − 1, xt и xt + 1.

При каждом t генерируется скрытое состояние, а также вывод. Обычно, если наша цель - предсказать yt + 2, то есть следующее наблюдение, мы хотим принять во внимание всю входную последовательность. Иными словами, мы хотим пройти через весь механизм обновления состояния. Таким образом, логичным было бы выбрать ot + 1 либо для прямого возврата из forward(), либо для дальнейшей обработки.

Действительно, return ot + 1 - это то, что Keras LSTM или GRU будет делать по умолчанию, если необязательный аргумент не передан. См. здесь для систематического сравнения возвращаемых значений RNN для обоих и Keras. Но в torch не так. В torch выходной тензор включает в себя все o. Вот почему на втором шаге выше мы выбираем единственный временной шаг, который нас интересует, а именно последний.

В следующих публикациях мы будем использовать больше, чем последний временной шаг. Иногда мы будем использовать последовательность скрытых состояний (hs) вместо выходов (os). Так что вы можете спросить, а что, если бы мы использовали здесь ht + 1 вместо ot + 1? Ответ: с GRU это не имело бы значения, поскольку эти двое идентичны. Однако LSTM сохраняет секунду, а именно «ячейку», stateAgain, см. этот пост для более подробной информации.

Немного об initialize(). Для простоты экспериментов мы создаем экземпляр GRU или LSTM на основе пользовательского ввода. Стоит отметить две вещи:

• Мы передаем batch_first = TRUE при создании RNN. Это требуется для RNN в torch, когда мы хотим, чтобы элементы последовательно укладывались в стопку в первом измерении. И мы этого действительно хотим; это, возможно, менее запутанно, чем изменение семантики измерения для одного подтипа модуля.
• num_layers можно использовать для создания составной RNN, соответствующей тому, что вы получили в Keras при связывании двух GRU/LSTM (первая создана с помощью return_sequences = TRUE). Этот параметр мы тоже включили для быстрого экспериментирования.

Давайте создадим модель для обучения. Это будет однослойная GRU из тридцати двух единиц.

# training RNNs on the GPU currently prints a warning that may clutter 
# the console
# see https://github.com/mlverse/torch/issues/461
# alternatively, use 
# device <- "cpu"
device <- torch_device(if (cuda_is_available()) "cuda" else "cpu")

net <- model("gru", 1, 32)
net <- net$to(device = device)

Обучение

После всей этой специфики RNN обучающий процесс полностью стандартный.

optimizer <- optim_adam(net$parameters, lr = 0.001)

num_epochs <- 30

train_batch <- function(b) {
  
  optimizer$zero_grad()
  output <- net(b$x$to(device = device))
  target <- b$y$to(device = device)
  
  loss <- nnf_mse_loss(output, target)
  loss$backward()
  optimizer$step()
  
  loss$item()
}

valid_batch <- function(b) {
  
  output <- net(b$x$to(device = device))
  target <- b$y$to(device = device)
  
  loss <- nnf_mse_loss(output, target)
  loss$item()
  
}

for (epoch in 1:num_epochs) {
  
  net$train()
  train_loss <- c()
  
  coro::loop(for (b in train_dl) {
    loss <-train_batch(b)
    train_loss <- c(train_loss, loss)
  })
  
  cat(sprintf("\nEpoch %d, training: loss: %3.5f \n", epoch, mean(train_loss)))
  
  net$eval()
  valid_loss <- c()
  
  coro::loop(for (b in valid_dl) {
    loss <- valid_batch(b)
    valid_loss <- c(valid_loss, loss)
  })
  
  cat(sprintf("\nEpoch %d, validation: loss: %3.5f \n", epoch, mean(valid_loss)))
}

Epoch 1, training: loss: 0.21908 

Epoch 1, validation: loss: 0.05125 

Epoch 2, training: loss: 0.03245 

Epoch 2, validation: loss: 0.03391 

Epoch 3, training: loss: 0.02346 

Epoch 3, validation: loss: 0.02321 

Epoch 4, training: loss: 0.01823 

Epoch 4, validation: loss: 0.01838 

Epoch 5, training: loss: 0.01522 

Epoch 5, validation: loss: 0.01560 

Epoch 6, training: loss: 0.01315 

Epoch 6, validation: loss: 0.01374 

Epoch 7, training: loss: 0.01205 

Epoch 7, validation: loss: 0.01200 

Epoch 8, training: loss: 0.01155 

Epoch 8, validation: loss: 0.01157 

Epoch 9, training: loss: 0.01118 

Epoch 9, validation: loss: 0.01096 

Epoch 10, training: loss: 0.01070 

Epoch 10, validation: loss: 0.01132 

Epoch 11, training: loss: 0.01003 

Epoch 11, validation: loss: 0.01150 

Epoch 12, training: loss: 0.00943 

Epoch 12, validation: loss: 0.01106 

Epoch 13, training: loss: 0.00922 

Epoch 13, validation: loss: 0.01069 

Epoch 14, training: loss: 0.00862 

Epoch 14, validation: loss: 0.01125 

Epoch 15, training: loss: 0.00842 

Epoch 15, validation: loss: 0.01095 

Epoch 16, training: loss: 0.00820 

Epoch 16, validation: loss: 0.00975 

Epoch 17, training: loss: 0.00802 

Epoch 17, validation: loss: 0.01120 

Epoch 18, training: loss: 0.00781 

Epoch 18, validation: loss: 0.00990 

Epoch 19, training: loss: 0.00757 

Epoch 19, validation: loss: 0.01017 

Epoch 20, training: loss: 0.00735 

Epoch 20, validation: loss: 0.00932 

Epoch 21, training: loss: 0.00723 

Epoch 21, validation: loss: 0.00901 

Epoch 22, training: loss: 0.00708 

Epoch 22, validation: loss: 0.00890 

Epoch 23, training: loss: 0.00676 

Epoch 23, validation: loss: 0.00914 

Epoch 24, training: loss: 0.00666 

Epoch 24, validation: loss: 0.00922 

Epoch 25, training: loss: 0.00644 

Epoch 25, validation: loss: 0.00869 

Epoch 26, training: loss: 0.00620 

Epoch 26, validation: loss: 0.00902 

Epoch 27, training: loss: 0.00588 

Epoch 27, validation: loss: 0.00896 

Epoch 28, training: loss: 0.00563 

Epoch 28, validation: loss: 0.00886 

Epoch 29, training: loss: 0.00547 

Epoch 29, validation: loss: 0.00895 

Epoch 30, training: loss: 0.00523 

Epoch 30, validation: loss: 0.00935 

Потери быстро уменьшаются, и, похоже, мы не видим переобучения на проверочном наборе.

Однако числа довольно абстрактны. Итак, мы воспользуемся набором тестов, чтобы увидеть, как на самом деле выглядит прогноз.

Оценка

Вот прогноз на январь 2014 года, по тридцать минут.

net$eval()

preds <- rep(NA, n_timesteps)

coro::loop(for (b in test_dl) {
  output <- net(b$x$to(device = device))
  preds <- c(preds, output %>% as.numeric())
})

vic_elec_jan_2014 <-  vic_elec %>%
  filter(year(Date) == 2014, month(Date) == 1) %>%
  select(Demand)

preds_ts <- vic_elec_jan_2014 %>%
  add_column(forecast = preds * train_sd + train_mean) %>%
  pivot_longer(-Time) %>%
  update_tsibble(key = name)

preds_ts %>%
  autoplot() +
  scale_colour_manual(values = c("#08c5d1", "#00353f")) +
  theme_minimal()

Рисунок 6. Прогнозы на один шаг вперед на январь 2014 г.

В целом прогноз отличный, но интересно посмотреть, как прогноз «упорядочивает» самые экстремальные пики. Этот вид «регресса к среднему» будет гораздо сильнее проявляться в более поздних настройках, когда мы попытаемся прогнозировать дальнейшее будущее.

Можем ли мы использовать нашу текущую архитектуру для многоэтапного прогнозирования? Можем.

Мы также можем вернуть текущий прогноз, то есть добавить его во входную последовательность, как только он станет доступен. Фактически, таким образом, для каждого элемента пакета мы получаем последовательность прогнозов в цикле.

Мы попытаемся спрогнозировать 336 временных шагов, то есть полную неделю.

n_forecast <- 2 * 24 * 7

test_preds <- vector(mode = "list", length = length(test_dl))

i <- 1

coro::loop(for (b in test_dl) {
  
  input <- b$x
  output <- net(input$to(device = device))
  preds <- as.numeric(output)
  
  for(j in 2:n_forecast) {
    input <- torch_cat(list(input[ , 2:length(input), ], output$view(c(1, 1, 1))), 

dim = 2)
    output <- net(input$to(device = device))
    preds <- c(preds, as.numeric(output))
  }
  
  test_preds[[i]] <- preds
  i <<- i + 1
  
})

Для визуализации возьмем три неперекрывающиеся последовательности.

test_pred1 <- test_preds[[1]]
test_pred1 <- c(rep(NA, n_timesteps), test_pred1, rep(NA, nrow(vic_elec_jan_2014) - 

n_timesteps - n_forecast))

test_pred2 <- test_preds[[408]]
test_pred2 <- c(rep(NA, n_timesteps + 407), test_pred2, rep(NA, 

nrow(vic_elec_jan_2014) - 407 - n_timesteps - n_forecast))

test_pred3 <- test_preds[[817]]
test_pred3 <- c(rep(NA, nrow(vic_elec_jan_2014) - n_forecast), test_pred3)


preds_ts <- vic_elec %>%
  filter(year(Date) == 2014, month(Date) == 1) %>%
  select(Demand) %>%
  add_column(
    iterative_ex_1 = test_pred1 * train_sd + train_mean,
    iterative_ex_2 = test_pred2 * train_sd + train_mean,
    iterative_ex_3 = test_pred3 * train_sd + train_mean) %>%
  pivot_longer(-Time) %>%
  update_tsibble(key = name)

preds_ts %>%
  autoplot() +
  scale_colour_manual(values = c("#08c5d1", "#00353f", "#ffbf66", "#d46f4d")) +
  theme_minimal()

Рисунок 7: Многоэтапные прогнозы на январь 2014 г., полученные в цикле.

Даже при использовании этой очень простой техники прогнозирования суточный ритм сохраняется, хотя и в сильно сглаженной форме. В прогнозе даже есть явная периодичность по дням недели. Однако мы действительно наблюдаем очень сильную регрессию к среднему значению, даже в тех случаях, когда сеть была «заполнена» входной последовательностью более высокого уровня.

Заключение

Надеюсь, этот пост предоставил полезное введение в прогнозирование временных рядов с помощью torch. Очевидно, мы выбрали сложный временной ряд: сложный, по крайней мере, по двум причинам:

• Чтобы правильно учесть тренд, необходима внешняя информация: внешняя информация в виде прогноза температуры, которую «на самом деле» можно было бы легко получить.
• Помимо очень важной трендовой составляющей, данные характеризуются несколькими уровнями сезонности.

Последнее не представляет проблемы для техник, с которыми мы здесь работаем. Если мы обнаружим, что какой-то уровень сезонности остался незамеченным, мы могли бы попытаться адаптировать текущую конфигурацию несколькими несложными способами:

• Используйте LSTM вместо GRU. Теоретически LSTM должна лучше улавливать дополнительные низкочастотные компоненты из-за своего вторичного хранилища, состояния ячейки.
• Сложите несколько слоев GRU/LSTM. Теоретически это должно позволить изучить иерархию временных характеристик, аналогично тому, что мы видим в сверточной нейронной сети.

Чтобы устранить первое препятствие, потребуются более серьезные изменения в архитектуре. Мы можем попытаться сделать это в более позднем «бонусном» посте. Но в следующих статьях мы сначала погрузимся в часто используемые методы прогнозирования последовательностей, а также перенесем на числовые временные ряды вещи, которые обычно выполняются при обработке естественного языка.

Оригинал: Introductory time-series forecasting with torch