Авторегрессионные модели скользящего среднего ARMA (p, q) для анализа временных рядов. Часть 1.

В прошлой статье мы рассмотрели случайные блуждания и белый шум как базовые модели временных рядов для определенных финансовых инструментов, таких как ежедневные цены на акции и индексы акций. Мы обнаружили, что в некоторых случаях модели случайного блуждания было недостаточно для отражения полного автокорреляционного поведения инструмента, что мотивирует применение более сложных моделей.

В следующих парах статей мы собираемся обсудить три типа моделей, а именно модель авторегрессии (AR) порядка p, модель скользящего среднего (MA) порядка q и модель смешанного автогрессивного скользящего среднего (ARMA) порядка p, q. Эти модели помогут нам попытаться уловить или «объяснить» больше серийной корреляции, присутствующей в инструменте. В конечном итоге они предоставят нам средство прогнозирования будущих цен.

Однако хорошо известно, что финансовые временные ряды обладают свойством, известным как кластеризация волатильности. То есть волатильность инструмента не постоянна во времени. Технический термин для этого поведения известен как условная гетероскедастичность. Поскольку модели AR, MA и ARMA не являются условно гетероскедастичными, то есть они не учитывают кластеризацию волатильности, нам в конечном итоге понадобится более сложная модель для наших прогнозов.

Такие модели включают модель с автогрессивной условной гетероскедастичностью (ARCH) и модель с обобщенной автогрессивной условной гетероскедастичностью (GARCH) и многие их варианты. GARCH особенно хорошо известна в области количественных финансов, и в основном используется для моделирования финансовых временных рядов как средство оценки риска.

Однако, как и во всех статьях QuantStart, я хочу построить эти модели на основе более простых версий, чтобы мы могли видеть, как каждый новый вариант меняет нашу способность к прогнозированию. Несмотря на то, что AR, MA и ARMA являются относительно простыми моделями временных рядов, они являются основой более сложных моделей, таких как интегрированное авторегрессионное скользящее среднее (ARIMA) и семейство GARCH. Следовательно, важно, чтобы мы их изучили.

Одна из наших первых торговых стратегий в серии статей о временных рядах будет заключаться в объединении ARIMA и GARCH для прогнозирования цен на n периодов вперед. Однако нам придется подождать, пока мы обсудим ARIMA и GARCH отдельно, прежде чем применять их к реальной стратегии!

Как мы будем действовать?

В этой статье мы собираемся обрисовать некоторые новые концепции временных рядов, которые нам понадобятся для остальных методов, а именно строгую стационарность и информационный критерий Акаике (AIC).

Вслед за этими новыми концепциями мы будем следовать традиционной схеме изучения новых моделей временных рядов:

Обоснование: первая задача - объяснить причину, по которой мы, как кванты, заинтересованы в конкретной модели. Почему мы вводим модель временных рядов? Какие эффекты она может улавливать? Что мы получаем (или теряем), добавляя дополнительную сложность?

Определение. Нам необходимо предоставить полное математическое определение (и соответствующие обозначения) модели временных рядов, чтобы свести к минимуму любую двусмысленность.

Свойства второго порядка: мы обсудим (и в некоторых случаях выведем) свойства второго порядка модели временных рядов, включая ее среднее значение, дисперсию и функцию автокорреляции.

Коррелограмма: мы будем использовать свойства второго порядка, чтобы построить коррелограмму реализации модели временных рядов, чтобы визуализировать ее поведение.

Моделирование: мы моделируем реализации модели временных рядов, а затем подгоняем модель к этим симуляциям, чтобы гарантировать, что у нас есть точные реализации и понимание процесса подбора.

Реальные финансовые данные: мы подгоним модель временных рядов к реальным финансовым данным и рассмотрим коррелограмму остатков, чтобы увидеть, как модель учитывает серийную корреляцию в исходном ряду.

Прогнозирование: мы создадим прогнозы модели временных рядов на n шагов вперед для конкретных реализаций, чтобы в конечном итоге получить торговые сигналы.

Почти все статьи, которые я пишу о моделях временных рядов, подпадают под этот шаблон, и это позволит нам легко сравнивать различия между каждой моделью по мере того, как мы добавляем дополнительную сложность.

Мы собираемся начать с рассмотрения строгой стационарности и AIC.

Строгая стационарность

Мы дали определение стационарности в статье о серийной корреляции. Однако, поскольку мы собираемся войти в сферу многих финансовых рядов с различной частотой, нам необходимо убедиться, что наши (возможные) модели учитывают изменяющуюся во времени волатильность этих рядов. В частности, необходимо учитывать их гетероскедастичность.

Мы столкнемся с этой проблемой, когда попытаемся подогнать определенные модели к историческим рядам. Как правило, не всю серийную корреляцию в остатках подобранных моделей можно учесть без учета гетероскедастичности. Это возвращает нас к стационарности. Ряд не является стационарным в дисперсии, если он по определению имеет изменяющуюся во времени волатильность.

Это мотивирует более строгое определение стационарности, а именно строгую стационарность:

Строго стационарный ряд

Модель временного ряда, {x_t}, является строго стационарной, если совместное статистическое распределение элементов x_t1,…, x_tn такое же, как для x_{t1 + m},…, x_{tn + m}, ∀ti, m.

Можно думать об этом определении просто как о том, что распределение временного ряда не изменяется при любом произвольном сдвиге во времени.

В частности, среднее значение и дисперсия постоянны во времени для строго стационарного ряда, а автоковариация между x_t и x_s (скажем) зависит только от абсолютной разности t и s, | t − s |.

В будущих публикациях мы будем возвращаться к строго стационарным рядам.

Информационный критерий Акаике

В предыдущих статьях я упоминал, что в конечном итоге нам нужно будет подумать о том, как выбирать между отдельными «лучшими» моделями. Это верно не только для анализа временных рядов, но и для машинного обучения и, в более широком смысле, для статистики в целом.

Два основных метода, которые мы будем использовать (на данный момент), это информационный критерий Акаике (AIC) и байесовский информационный критерий (по мере продвижения наших статей по байесовской статистике).

Мы кратко рассмотрим AIC, поскольку он будет использоваться во второй части статьи ARMA.

AIC - это, по сути, инструмент, помогающий в выборе модели. То есть, если у нас есть набор статистических моделей (включая временные ряды), то AIC оценивает «качество» каждой модели по сравнению с другими, которые у нас есть.

Он основан на теории информации, которая является очень интересной и глубокой темой, о которой, к сожалению, мы не можем вдаваться в подробности. Он пытается сбалансировать сложность модели, которая в данном случае означает количество параметров, с тем, насколько хорошо она соответствует данным. Дадим определение:

Информационный критерий Акаике

Если мы возьмем функцию правдоподобия для статистической модели, которая имеет k параметров, а L максимизирует правдоподобие, то информационный критерий Акаике определяется следующим образом:

AIC=−2log(L)+2k

Предпочтительная модель из ряда моделей имеет минимальный AIC в группе. Вы можете видеть, что AIC растет с увеличением числа параметров k, но уменьшается, если увеличивается отрицательная логарифмическая вероятность. По сути, это наказание для переобученных моделей.

Мы собираемся создать модели AR, MA и ARMA различного порядка, и один из способов выбрать «лучшую» модель, подходящую для конкретного набора данных, использовать AIC. Это то, что мы будем делать в следующей статье, в первую очередь для моделей ARMA.

Авторегрессионные (AR) модели порядка p

Первая модель, которую мы собираемся рассмотреть, которая составляет основу части 1, это модель авторегрессии порядка p, часто сокращаемая до AR(p).

Обоснование

В предыдущей статье мы рассмотрели случайное блуждание, где каждый член xt зависит исключительно от предыдущего члена xt − 1 и члена стохастического белого шума wt:

xt = xt−1 + wt

Модель авторегрессии - это просто расширение случайного блуждания, которое включает члены, находящиеся дальше во времени. Структура модели является линейной, то есть модель линейно зависит от предыдущих членов с коэффициентами для каждого члена. Вот откуда «регрессия» в «авторегрессии». По сути, это регрессионная модель, в которой предыдущие члены являются предикторами.

Модель авторегрессии порядка p

Модель временного ряда, {xt}, является авторегрессионной моделью порядка p, AR (p), если:

Где {wt} - белый шум, а αi∈R, где αp ≠ 0 для процесса авторегрессии p-порядка.

Если мы рассмотрим оператор обратного сдвига B (см. предыдущую статью), то мы можем переписать приведенное выше уравнение как функцию θ от B:

Возможно, первое, на что следует обратить внимание в модели AR(p), это то, что случайное блуждание - это просто AR(1) с α1, равным единице. Как мы заявляли выше, модель авторегрессии является продолжением случайного блуждания, поэтому в этом есть смысл!

С помощью модели AR(p) легко делать прогнозы для любого времени t, так как после определения коэффициентов αi наша оценка вычисляется просто:

Следовательно, мы можем делать прогнозы на n шагов вперед, вычисляя соответствующие значения. Фактически, как только мы рассмотрим модели ARMA в части 2, мы будем использовать функцию predict в R для создания прогнозов (вместе с диапазонами доверительных интервалов стандартной ошибки), которые помогут нам создавать торговые сигналы.

Стационарность процессов авторегрессии

Одним из наиболее важных аспектов модели AR (p) является то, что она не всегда стационарна. Действительно, стационарность конкретной модели зависит от параметров. Я уже говорил об этом в предыдущей статье.

Чтобы определить, является ли процесс AR (p) стационарным или нет, нам необходимо решить характеристическое уравнение. Характеристическое уравнение - это просто модель авторегрессии, записанная в форме обратного сдвига, установленного на ноль:

θp(B)=0

Мы решаем это уравнение относительно B. Чтобы конкретный процесс авторегрессии был стационарным, нам нужно, чтобы все абсолютные значения корней этого уравнения превышали единицу. Это чрезвычайно полезное свойство, позволяющее быстро вычислить, является процесс AR(p) стационарным или нет.

Давайте рассмотрим несколько примеров, чтобы конкретизировать эту идею:

Случайное блуждание. Процесс AR(1) с α1 = 1 имеет характеристическое уравнение θ = 1 − B. Ясно, что он имеет корень B = 1 и как таковой не является стационарным.

AR(1) - если мы выберем α1 = 14, мы получим xt = 14xt−1 + wt. Это дает нам характеристическое уравнение 1−14B = 0, которое имеет корень B = 4>1, и поэтому этот конкретный процесс AR (1) является стационарным.

AR(2) - если мы положим α1 = α2 = 12, то получим xt = 12xt−1 + 12xt−2 + wt. Его характеристическое уравнение принимает вид −12(B − 1)(B + 2) = 0, что дает два корня B = 1, −2. Поскольку он имеет единичный корень, это нестационарный ряд. Однако другие ряды AR (2) могут быть стационарными.

Свойства второго порядка

Среднее значение процесса AR(p) равно нулю. Однако автоковариации и автокорреляции задаются рекурсивными функциями, известными как уравнения Юла-Уокера. Полные свойства приведены ниже:

Обратите внимание, что перед вычислением автокорреляций необходимо знать значения параметра αi.

Теперь, когда мы сформулировали свойства второго порядка, мы можем моделировать различные порядки AR(p) и строить соответствующие коррелограммы.

Моделирование и коррелограммы

AR(1)

Начнем с процесса AR(1). Это похоже на случайное блуждание, за исключением того, что α1 не обязательно равно единице. Наша модель будет иметь α1 = 0,6. Код R для создания этой симуляции следующий:

> set.seed(1)
> x <- w <- rnorm(100)
> for (t in 2:100) x[t] <- 0.6*x[t-1] + w[t]

Обратите внимание, что наш цикл for выполняется от 2 до 100, а не от 1 до 100, поскольку x[t-1] не индексируется, когда t = 0. Аналогично для процессов AR(p) более высокого порядка t в этом цикле должно находиться в диапазоне от p до 100.

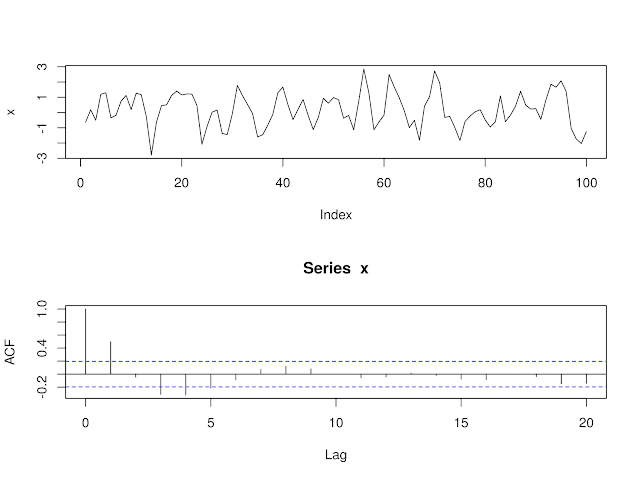
Мы можем построить реализацию этой модели и связанную с ней коррелограмму, используя функцию layout:

> layout(1:2)
> plot(x, type="l")
> acf(x)

Реализация модели AR (1) с α1 = 0,6 и соответствующей коррелограммой

Давайте теперь попробуем подогнать процесс AR(p) к смоделированным данным, которые мы только что сгенерировали, чтобы посмотреть, сможем ли мы восстановить базовые параметры. Как вы помните, мы проводили аналогичную процедуру в статье о белом шуме и случайных блужданиях.

Как оказалось, R предоставляет полезную команду ar для подгонки моделей авторегрессии. Мы можем использовать этот метод, чтобы сначала сообщить нам наилучший порядок p модели (как определено AIC выше) и предоставить нам оценки параметров для αi, которые мы затем можем использовать для формирования доверительных интервалов.

Для полноты картины воссоздадим ряд x:

> set.seed(1)
> x <- w <- rnorm(100)
> for (t in 2:100) x[t] <- 0.6*x[t-1] + w[t]

Теперь мы используем команду ar, чтобы подогнать модель авторегрессии к смоделированному процессу AR(1), используя оценку максимального правдоподобия (MLE) в качестве процедуры подбора.

Сначала извлечем наилучший полученный порядок:

> x.ar <- ar(x, method = "mle")
> x.ar$order

1

Команда ar успешно определила, что наша базовая модель временных рядов является процессом AR(1).

Затем мы можем получить оценки параметра(ов) αi:

> x.ar$ar

0.5231187

Процедура MLE дала оценку α1 = 0,523, что немного ниже истинного значения α1 = 0,6.

Наконец, мы можем использовать стандартную ошибку (с асимптотической дисперсией) для построения 95% доверительных интервалов вокруг базового параметра(ов). Для этого мы просто создаем вектор c(-1,96, 1,96), а затем умножаем его на стандартную ошибку:

x.ar$ar + c(-1.96, 1.96)*sqrt(x.ar$asy.var)

0.3556050 0.6906324

Истинный параметр действительно попадает в 95% доверительный интервал, как и следовало ожидать, исходя из того факта, что мы создали реализацию на основе модели.

Как насчет того, чтобы изменить α1 = −0,6?

> set.seed(1)
> x <- w <- rnorm(100)
> for (t in 2:100) x[t] <- -0.6*x[t-1] + w[t]
> layout(1:2)
> plot(x, type="l")
> acf(x)

Реализация модели AR(1) с α1 = −0,6 и соответствующей коррелограммой

Как и раньше, мы можем подогнать модель AR(p) с помощью ar:

> set.seed(1)
> x <- w <- rnorm(100)
> for (t in 2:100) x[t] <- -0.6*x[t-1] + w[t]
> x.ar <- ar(x, method = "mle")
> x.ar$order

1

> x.ar$ar

-0.5973473

> x.ar$ar + c(-1.96, 1.96)*sqrt(x.ar$asy.var)

-0.7538593 -0.4408353

Мы снова восстанавливаем правильный порядок модели с очень хорошей оценкой α1 = - 0,597 от α1 = −0,6. Мы также видим, что истинный параметр снова попадает в доверительный интервал 95%.

AR(2)

Давайте добавим немного сложности нашим процессам авторегрессии, моделируя модель порядка 2. В частности, мы установим α1 = 0,666, но также установим α2 = −0,333. Вот полный код для моделирования и построения графика, а также коррелограмма для такого ряда:

> set.seed(1)
> x <- w <- rnorm(100)
> for (t in 3:100) x[t] <- 0.666*x[t-1] - 0.333*x[t-2] + w[t]
> layout(1:2)
> plot(x, type="l")
> acf(x)

Реализация модели AR(2) с α1 = 0,666, α2 = −0,333 и соответствующей коррелограммой.

Как и прежде, мы видим, что коррелограмма значительно отличается от коррелограммы белого шума, как и следовало ожидать. Есть статистически значимые пики при k = 1, k = 3 и k = 4.

Еще раз, мы собираемся использовать команду ar, чтобы подогнать модель AR(p) к нашей базовой реализации AR(2). Процедура аналогична подгонке AR(1):

> set.seed(1)
> x <- w <- rnorm(100)
> for (t in 3:100) x[t] <- 0.666*x[t-1] - 0.333*x[t-2] + w[t]
> x.ar <- ar(x, method = "mle")
Warning message:
In arima0(x, order = c(i, 0L, 0L), include.mean = demean) :
  possible convergence problem: optim gave code = 1
> x.ar$order

2

> x.ar$ar

0.6961005 -0.3946280

Восстановлен правильный порядок, и оценки параметров: α1 = 0,696 и α2 = - 0,395 не слишком далеки от истинных значений параметров α1 = 0,666 и α2 = −0,333.

Обратите внимание, что мы получаем предупреждающее сообщение о конвергенции. Также обратите внимание, что R фактически использует функцию arima0 для вычисления модели AR. Как мы узнаем из последующих статей, модели AR(p) - это просто модели ARIMA(p, 0, 0), и, таким образом, модель AR является частным случаем ARIMA без компонента скользящей средней (MA).

Мы также будем использовать команду arima для создания доверительных интервалов вокруг нескольких параметров, поэтому мы не сделали этого здесь.

Теперь, когда мы создали некоторые смоделированные данные, пришло время применить модели AR(p) к временным рядам финансовых активов.

Финансовые данные

Amazon Inc.

Начнем с получения цены акций Amazon (AMZN) с помощью Quantmod:

> require(quantmod)
> getSymbols("AMZN")
> AMZN

..
..
2015-08-12    523.75    527.50   513.06     525.91     3962300        525.91
2015-08-13    527.37    534.66   525.49     529.66     2887800        529.66
2015-08-14    528.25    534.11   528.25     531.52     1983200        531.52

Первая задача - всегда составлять график цены для краткого визуального осмотра. В этом случае мы будем использовать дневные цены закрытия:

> plot(Cl(AMZN))

Вы заметите, что Quantmod добавляет для нас некоторое форматирование, а именно дату и немного более красивую диаграмму, чем обычные диаграммы R:

Дневная цена закрытия AMZN

Теперь мы возьмем логарифмическую доходность AMZN, а затем разность первого порядка ряда, чтобы преобразовать исходный ценовой ряд из нестационарного ряда в (потенциально) стационарный.

Это позволяет нам сравнивать «яблоки с яблоками» между акциями, индексами или любым другим активом для использования в более поздней многомерной статистике, например, при вычислении ковариационной матрицы. Если вам нужно подробное объяснение того, почему предпочтительнее логарифмическая доходность, прочтите эту статью на Quantivity.

Давайте создадим новый ряд amznrt для хранения нашей логарифмической доходности:

> amznrt = diff(log(Cl(AMZN)))

И снова мы можем построить график ряда:

> plot(amznrt)

Разность первого порядка дневных логарифмических доходностей  для цен закрытия AMZN

На этом этапе мы хотим построить коррелограмму. Мы смотрим, выглядит ли ряд разностей как белый шум. В противном случае возникает необъяснимая серийная корреляция, которую можно «объяснить» авторегрессионной моделью.

> acf(amznrt, na.action=na.omit)

Коррелограмма разности первого порядка дневной логарифмической доходности цен закрытия AMZN

Мы замечаем статистически значимый пик при k = 2. Следовательно, существует разумная возможность необъяснимой серийной корреляции. Однако имейте в виду, что это может быть связано с систематической ошибкой выборки. Таким образом, мы можем попробовать подогнать модель AR(p) к ряду и получить доверительные интервалы для параметров:

> amznrt.ar <- ar(amznrt, na.action=na.omit)
> amznrt.ar$order

2

> amznrt.ar$ar

-0.02779869 -0.06873949

> amznrt.ar$asy.var

            [,1]        [,2]
[1,] 4.59499e-04 1.19519e-05
[2,] 1.19519e-05 4.59499e-04

Подгонка модели ar авторегрессии к разностным рядам логарифмических цен первого порядка дает модель AR (2) с α1 = - 0,0278 и α2 = - 0,0687. Я также вывел асимптотическую дисперсию, чтобы мы могли вычислить стандартные ошибки для параметров и получить доверительные интервалы. Мы хотим увидеть, является ли ноль частью 95% доверительного интервала, как будто это снижает нашу уверенность в том, что у нас есть истинный базовый процесс AR(2) для серии AMZN.

Чтобы вычислить доверительные интервалы на уровне 95% для каждого параметра, мы используем следующие команды. Мы извлекаем квадратный корень из первого элемента матрицы асимптотической дисперсии, чтобы получить стандартную ошибку, затем создаем доверительные интервалы, умножая его на -1,96 и 1,96 соответственно, для уровня 95%:

> -0.0278 + c(-1.96, 1.96)*sqrt(4.59e-4)

-0.0697916  0.0141916

> -0.0687 + c(-1.96, 1.96)*sqrt(4.59e-4)

-0.1106916 -0.0267084

Обратите внимание, что это становится более простым при использовании функции arima, но мы дождемся части 2, прежде чем вводить ее должным образом.

Таким образом, мы можем видеть, что для α1 ноль содержится в доверительном интервале, а для α2 ноль не содержится в доверительном интервале. Следовательно, мы должны быть очень осторожны, думая, что у нас действительно есть основная генеративная модель AR(2) для AMZN.

В частности, отметим, что модель авторегрессии не учитывает кластеризацию волатильности, которая приводит к кластеризации серийной корреляции в финансовых временных рядах. Когда мы рассмотрим модели ARCH и GARCH в следующих статьях, мы учтем это.

Когда мы перейдем к использованию полной функции arima в следующей статье, мы сделаем прогнозы на основе дневных ценовых рядов, чтобы позволить нам создавать торговые сигналы.

Индекс акций США S&P500

Наряду с отдельными акциями мы также можем рассмотреть индекс акций США, S&P500. Применим все предыдущие команды к этому ряду и построим графики, как и раньше:

> getSymbols("^GSPC")
> GSPC

..
..
2015-08-12   2081.10   2089.06  2052.09    2086.05  4269130000       2086.05
2015-08-13   2086.19   2092.93  2078.26    2083.39  3221300000       2083.39
2015-08-14   2083.15   2092.45  2080.61    2091.54  2795590000       2091.54

Мы можем построить графики цен:

> plot(Cl(GSPC))

Дневная цена закрытия S&500

Как и раньше, создадим разность первого порядка логарифмических цен закрытия:

> gspcrt = diff(log(Cl(GSPC)))

И снова мы можем построить график ряда:

> plot(gspcrt)

Разность первого порядка дневных логарифмических доходностей для цен закрытия S&500

Из этого графика видно, что волатильность не является стационарной во времени. Это также отражено на графике коррелограммы. Есть много пиков, включая k = 1 и k = 2, которые статистически значимы за пределами модели белого шума.

Кроме того, мы видим доказательства процессов длинной памяти, поскольку есть некоторые статистически значимые пики при k = 16, k = 18 и k = 21:

> acf(gspcrt, na.action=na.omit)

Коррелограмма разности первого порядка дневной логарифмической доходности цен закрытия S&500.

В конечном итоге нам понадобится более сложная модель, чем модель авторегрессии порядка p. Однако на данном этапе мы еще можем попробовать подогнать такую модель. Посмотрим, что мы получим, если так сделаем:

> gspcrt.ar <- ar(gspcrt, na.action=na.omit)
> gspcrt.ar$order

22

> gspcrt.ar$ar

 [1] -0.111821507 -0.060150504  0.018791594 -0.025619932 -0.046391435
 [6]  0.002266741 -0.030089046  0.030430265 -0.007623949  0.044260402
[11] -0.018924358  0.032752930 -0.001074949 -0.042891664 -0.039712505
[16]  0.052339497  0.016554471 -0.067496381  0.007070516  0.035721299
[21] -0.035419555  0.031325869

Использование ar дает модель AR(22), то есть модель с 22 ненулевыми параметрами! Что это говорит нам? Показательно, что серийная корреляция, вероятно, намного сложнее, чем может реально объяснить простая линейная модель прошлых цен.

Однако мы уже знали об этом, потому что видим значительную последовательную корреляцию в волатильности. Например, рассмотрим очень нестабильный период около 2008 года.

Это мотивирует следующий набор моделей, а именно скользящую среднюю MA(q) и авторегрессионную скользящую среднюю ARMA(p, q). Мы узнаем об обоих из них во второй части этой статьи. Как мы неоднократно упоминали, это в конечном итоге приведет нас к семейству моделей ARIMA и GARCH, обе из которых будут намного лучше соответствовать сложности последовательной корреляции S&500.

Это позволит нам значительно улучшить наши прогнозы и в конечном итоге разработать более прибыльные стратегии.

Оригинал: Autoregressive Moving Average ARMA(p, q) Models for Time Series Analysis