Использование индекса фрактальной размерности для прогнозирования рыночных максимумов и минимумов

Рынки фрактальны по своей природе, то есть, они обладают определенными свойствами, такими как самоподобие, что позволяет моделировать их с использованием инструментов из этой области. Конечно, легче сказать, чем сделать. В этой статье мы попытаемся разработать индекс фрактальной размерности на основе функции экспоненты Херста, чтобы увидеть, как мы можем предсказать, когда рыночные тенденции вот-вот изменятся. Прежде чем перейти к индексу фрактальной размерности, мы начнем с введения и кодирования экспоненты Херста.

Показатель Херста

Поведение финансовых активов чередуются между импульсом и возвратом к среднему значению при изменении режимов и бизнес-циклов. Один из способов узнать, возвращаются ли рынки к среднему или имеют тренд (таким образом, преобладает импульс), это использовать показатель Херста.

Можно наблюдать три основных типа движения цены финансовых активов: тренд, возврат к среднему и случайное блуждание.

Временной ряд в тренде - это тот, который увеличивается или уменьшается с течением времени. Основная характеристика - положительная автокорреляция.

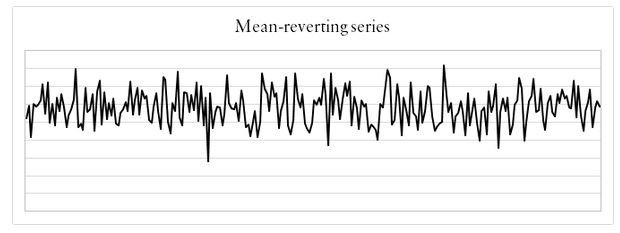
Временной ряд с возвратом к среднему - это тот временной ряд, который колеблется вокруг своего долгосрочного равновесия. Основная характеристика - отрицательная автокорреляция.

Временной ряд случайного блуждания - это ряд, который перемещается случайным образом во времени. Основная характеристика - нулевая автокорреляция.

Теория случайного блуждания является основой количественных финансов и является одной из первых вещей, которые должен понять практикующий специалист. Предполагается, что финансовые активы следуют случайному блужданию, а это означает, что движения цен случайны и не могут быть спрогнозированы с использованием их прошлых значений. Наша цель здесь - понять, какой из трех типов является основной характеристикой наших проанализированных данных, и на этот вопрос можно ответить с помощью показателя Херста.

Чтобы кратко определить этот показатель, он был создан британским гидрологом Эдвином Херстом во время исследования реки Нил в Египте. Мы можем интерпретировать его тремя способами:

Когда H <0,5, мы можем сказать, что наши данные возвращаются к среднему.

Когда H = 0,5, мы можем сказать, что наши данные случайны.

Когда H> 0,5, мы можем сказать, что наши данные имеют тренд.

Hurst = 0.4978.

Hurst = 0.0016.

Hurst = 0.9488.

Если мы рассчитаем показатель Херста на основе реальных данных, например, индекса S&P500 между 2007 и 2019 годами, мы обнаружим, что он составляет около 0,43. Означает ли это, что индекс возвращается к среднему?

Необязательно, рассчитанное значение относится к периоду 2007–2019 гг. и имеет диапазон из 30 значений, которые могут не отражать всей истории. Истинное значение должно находиться в диапазоне от 0,49 до 0,51, что ближе к случайному блужданию с долей детерминизма. Мы не можем отрицать возможность того, что S&P500 не следует какой-либо определенной закономерности, и хотя мы знаем, что время от времени это происходит (в основном в тренде), мы просто хотим узнать, как использовать показатель Херста для быстрых статистических тестов, при условии, что мы используем качественные данные и оптимальные параметры, такие как выбор соответствующих периодов времени. Другой реальный пример - денежная масса M2 в США. Естественно, он всегда имеет наклон вверх.

Hurst = 0.7445.

Очевидно, что это тренд в течение всего анализируемого промежутка времени, но что говорит экспонента? Согласно показанным результатам, показатель Херста составляет около 0,744, что указывает на высокотрендовый ряд. С математической точки зрения, показатель Херста основан на идее использования дисперсии логарифмического ряда цен для определения диффузии. Что делает функция, так это сравнивает распространение временного ряда с диффузией геометрического броуновского движения, другими словами, если данные обладают автокорреляцией, то приведенное ниже соотношение не будет соблюдаться и может быть изменено, чтобы включить значение 2H, которым на самом деле является показатель Херста:

Если H = 0,5, то уравнение сводится к следующему:

Это скорость диффузии геометрического броуновского движения. Tau() обозначает время, и оно равно дисперсии на более длительном временном горизонте. Геометрическое броуновское движение диктует, что дисперсия равна временному горизонту, когда он достаточно велик. Теперь становится ясно, почему мы говорим, что, когда показатель Херста равен 0,5, мы имеем случайный временной ряд.

Чтобы вычислить скользящую меру экспоненты Херста, нам нужно сначала установить библиотеку:

pip install hurst

Затем мы можем создать функцию, как показано ниже:

from hurst import compute_Hcdef hurst(Data, lookback, what, where):for i in range(len(Data)):
        try:
            new = Data[i - lookback:i, what]
            
            Data[i, where] = compute_Hc(Data[i - lookback:i + 1, what])[0]
        except ValueError:
            pass
        
    return Data# Using the Function
my_data = hurst(my_data, 100, 3, 4)

EURUSD на первой панели с экспонентой Херста на второй панели.

Каждый раз, когда рынок начинает тренд, его экспонента Херста начинает расти из-за устойчивости, пока рынки не начнут консолидироваться, а именно тогда, когда Херст начнет падать. Идея обнаружения вершин в экспоненте Херста для обнаружения поворотных точек рынка кажется разумной, но на практике она не очень полезна, поскольку экспонента Херста на самом деле не следует четкой стационарной модели. Вчерашний барьер 0,60 - это бессмысленный уровень сегодня.

Индекс фрактальной размерности

Индекс измеряет, насколько нерегулярны временные ряды. Когда наблюдается сильный тренд, естественно, рыночная цена приближается к одномерной линии, а индекс фрактальной размерности приближается к 1,0. Когда рынок нестабилен и движется вбок, индекс фрактальной размерности приближается к 2,0.

Фрактальную размерность можно легко вычислить из экспоненты Херста, используя следующую формулу:

EURUSD на первой панели и индекс фрактальной размерности на второй панели.

Следовательно, код можно изменить на следующий:

def fractal_dimension_index(Data, lookback, what, where):for i in range(len(Data)):
        try:
            new = Data[i - lookback:i, what]
            
            Data[i, where] = compute_Hc(Data[i - lookback:i + 1, what])[0]
            Data[i, where] = 2 - Data[i, where]
            
        except ValueError:
            pass    return Data

GBPUSD на первой панели с индексом фрактальной размерности на второй панели.

Использование индекса фрактальной размерности

На самом деле не существует четкой торговой стратегии, которую можно было бы сформировать на основе индекса фрактальной размерности. Лучше всего проверить крайние минимумы около 1,25/1,20, чтобы увидеть, будет ли текущая тенденция сломана или нет. Проще говоря:

• Всякий раз, когда рынок имеет нисходящий тренд и индекс фрактальной размерности достигает 1,25/1,20, нам следует быть осторожными, поскольку мы, вероятно, входим в фазу дна.
• Когда на рынке наблюдается восходящий тренд, а индекс фрактальной размерности достигает 1,25/1,20, нам следует быть осторожными, поскольку мы, вероятно, входим в фазу максимума.

График сигналов на EURUSD сформирован по сигналам от Fractal Dimension Index.

График сигналов на GBPUSD сформирован по сигналам от Fractal Dimension Index.

def signal(Data, fdi, trend, buy, sell):
    
  for i in range(len(Data)):
            
     if Data[i, fdi] < lower_barrier and Data[i, what] < Data[i - trend, what] and Data[i - 1, fdi] > lower_barrier:
            Data[i, buy] = 1
            
     if Data[i, fdi] < lower_barrier and Data[i, what] > Data[i - trend, what] and Data[i - 1, fdi] > lower_barrier:
            Data[i, sell] = -1# The trend variable is to help the algorithm know whether the market has been trending up or down

Возврат к экспоненте Херста

Как мы можем использовать экспоненту Херста в торговле, если у нее нет прогностических свойств?

Предположим, у вас есть период, который нужно оценить после использования стратегии или модели, происходящей из семейства систем следования за трендом, а затем вы посмотрите на экспоненту Херста этого периода и заметите, что она составляет около 0,389, что означает возврат к среднему значению. Вы можете сделать вывод, что вы не можете сказать, что использованная стратегия плохая, но рыночная структура этого периода не подходила для модели, и поэтому лучше протестировать ее на трендовом рынке, чтобы полностью узнать ее прибыльность. Что вы знаете наверняка, так это то, что ваша стратегия не адаптирована ко всем типам рынков, и это уже полезная информация, извлеченная из экспоненты Херста.

Аналогичный инструмент: индикатор Fractal

В предыдущей статье мы обсуждали индикатор Fractal, который отличается от того, который обсуждался выше. Британский гидролог Гарольд Эдвин Херст ввел меру изменчивости временных рядов за анализируемый период времени. Этот показатель называется Rescaled Range Analysis, и он является основой нашего индикатора Fractal. Вот как рассчитать Rescaled Range Analysis:

Формула Rescaled Range очень интересна, поскольку она учитывает волатильность (S), среднее значение (X-bar) и диапазон данных для анализа ее свойств. Приведенная выше формула говорит о том, что мы должны вычислить диапазон между мини-диапазонами максимального и минимального значений, а затем разделить их на стандартное отклонение, которое в данном случае является показателем волатильности.

Поскольку я вечный поклонник самостоятельной работы и самостоятельной настройки, я изменил формулу, чтобы она имела следующий смысл, который мы позже вместе увидим в пошаговом методе:

Объединение максимумов и минимумов может дать нам более четкую картину волатильности, поэтому сначала мы рассчитаем экспоненциальную скользящую среднюю как минимумов, так и максимумов за предыдущий период X, а затем рассчитаем их соответствующее стандартное отклонение, то есть волатильность. Затем мы вычислим первый диапазон, в котором мы вычтем текущий максимум из среднего максимума, измеренного экспоненциальной скользящей средней на первом этапе, а затем сделаем то же самое с минимумом. После этого мы вычислим скользящий максимум для первого диапазона (максимум минус его среднее значение) и скользящий минимум для второго диапазона (минимум минус его среднее значение). Затем мы вычитаем скользящий максимум из скользящего минимума перед изменением масштаба путем деления результата на среднее значение между двумя стандартными отклонениями, рассчитанными выше для максимумов и минимумов.

Все это делается с помощью следующей функции, для которой требуется массив OHLC с несколькими свободными столбцами:

def fractal_indicator(Data, high, low, ema_lookback, min_max_lookback, where):

Data = ema(Data, 2, ema_lookback, high, where)
Data = ema(Data, 2, ema_lookback, low, where + 1)

Data = volatility(Data, ema_lookback, high, where + 2)
Data = volatility(Data, ema_lookback, low, where + 3)

Data[:, where + 4] = Data[:, high] - Data[:, where]
Data[:, where + 5] = Data[:, low] - Data[:, where + 1]for i in range(len(Data)):
try:
Data[i, where + 6] = max(Data[i - min_max_lookback + 1:i + 1, where + 4])

except ValueError:
pass

for i in range(len(Data)):
try:
Data[i, where + 7] = min(Data[i - min_max_lookback + 1:i + 1, where + 5])

except ValueError:
pass

Data[:, where + 8] = (Data[:, where + 2] + Data[:, where + 3]) / 2
Data[:, where + 9] = (Data[:, where + 6] - Data[:, where + 7]) / Data[:, where + 8]

return Data

Итак, становится ясно, что индикатор Fractal - это просто переработанная версия формулы Rescaled Range, созданной Гарольдом Херстом.

Если вы хотите добавить столбцы в свой массив, вы можете использовать следующую функцию:

def adder(Data, times):

for i in range(1, times + 1):

z = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, z, axis = 1)return Data

Почасовые данные EURUSD на первой панели и индикатор Fractal (20, 14) на второй панели.

Мы должны понять, как использовать индикатор Fractal. Из графика ясно, что мы можем найти экстремальные значения около минимума, который составляет 1,00 (или немного ниже, в зависимости от параметров, используемых ниже). Мы можем назвать это фрактальным порогом.

Следовательно, разумная торговая стратегия может иметь следующие условия:

• Каждый раз, когда индикатор Fractal достигает порога 1,00, когда рыночная цена имеет тенденцию к снижению, мы можем ожидать, что произойдет структурный сдвиг рыночной цены, то есть краткосрочный разворот вверх. Мы должны открыть длинную позицию.
• Каждый раз, когда индикатор Fractal достигает порога 1,00, когда рыночная цена имеет тенденцию к повышению, мы можем ожидать, что произойдет структурный сдвиг рыночной цены, то есть краткосрочный разворот вниз. Мы должны открыть короткую позицию.

trend = 10
def signal(Data, what, closing, buy, sell):
    
    for i in range(len(Data)):
            
     if Data[i, what] < barrier and Data[i, closing] < Data[i - trend, closing]:
        Data[i, buy] = 1
            
     if Data[i, what] < barrier and Data[i, closing] > Data[i - trend, closing]:  
        Data[i, sell] = -1# The trend variable is the algorithm's way to see whether the market price has been trending down or up. This is to known what position to initiate (long/short) as the Fractal Indicator only shows a uniform signal which is the event of reaching 1.00
# The Data variable refers to the OHLC array
# The what variable refers to the Fractal Indicator
# The closing variable refers to the closing price
# The buy variable refers to where we should place long orders
# The sell variable refers to where we should place short orders

Стоит отметить, что мы можем разработать миниатюрную номенклатуру для описания индикатора Fractal. Обратите внимание, что у нас есть две переменные: период ретроспективного анализа для экспоненциальной скользящей средней и период ретроспективного анализа для периода диапазона нормализации:

Первая переменная - это просто период расчета скользящей средней.

Вторая переменная - это просто период диапазона наблюдений.

Следовательно, индикатор Fractal с периодом экспоненциальной скользящей средней 20 и периодом ретроспективного обзора нормализации 14 может быть записан как FI (20, 14).

Данные USDCHF M15 на первой панели и индикатор Fractal (20, 14) на второй панели.

Нам нужна функция Exponential Moving Average для работы указанного выше индикатора. Ее можно рассчитать следующим образом:

def ma(Data, lookback, what, where):
    
    for i in range(len(Data)):
      try:
        Data[i, where] = (Data[i - lookback + 1:i + 1, what].mean())
        
            except IndexError:
                pass
    return Datadef ema(Data, alpha, lookback, what, where):
    
    # alpha is the smoothing factor
    # window is the lookback period
    # what is the column that needs to have its average calculated
    # where is where to put the exponential moving average
    
    alpha = alpha / (lookback + 1.0)
    beta  = 1 - alpha
    
    # First value is a simple SMA
    Data = ma(Data, lookback, what, where)
    
    # Calculating first EMA
    Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)    # Calculating the rest of EMA
    for i in range(lookback + 2, len(Data)):
            try:
                Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
        
            except IndexError:
                pass
    return Data

Заключение

Почему была написана эта статья? Это, конечно, не метод кормления с ложечки и не путь к прибыльной стратегии. Если вы будете следить за моими статьями, вы заметите, что я больше акцентирую внимание на том, как это сделать, и что я также предоставляю функции, а не полный воспроизводимый код. В финансовой индустрии вы должны сами комбинировать кусочки информации и данных, только тогда вы овладеете искусством исследования и торговли.

Я всегда советую вам проводить надлежащие бэк-тесты и понимать любые риски, связанные с торговлей.

Оригинал: The Fractal Dimension Index on Predicting Market Tops & Bottoms