Использование комплексных чисел в R

В данной статье я хочу рассмотреть использование комплексных чисел в R. Как всегда, если вы заинтересованы в изучении математики комплексных чисел, я бы начал с просмотра ссылок в интернете. На первый взгляд это руководство показалось мне хорошим, хотя я не могу утверждать, что прочитал его.

Поскольку комплексные числа реализованы в пакете «base», начать с ними работать очень легко. Чтобы построить комплексное число x + iy, вы используете функцию complex:

x <- 1
y <- 1
z <- complex(real = x, imaginary = y)
z
# [1] 1+1i

В математике принято использовать z для обозначения комплексного числа, поэтому я продолжу эту традицию.

Как всегда бывает с математическими типами данных в R, вы можете преобразовать другие объекты в класс «complex», используя функцию as.complex:

as.complex(-1)
# [1] -1+0i

И вы можете проверить, является ли объект комплексным, с помощью is.complex:

is.complex(as.complex(-1))
# [1] TRUE

Помимо этих стандартных операций, есть пять основных математических операций, которые вы можете использовать с комплексными числами.

Во-первых, вы хотите иметь возможность извлекать действительные и мнимые компоненты комплексного числа. Вы можете сделать это с помощью Re и Im соответственно:

z <- complex(real = 2, imaginary = 1)
Re(z)
# [1] 2
Im(z)
# [1] 1

Представление чисел (x, y) поначалу легче понять, но представление в полярных координатах часто бывает более практичным. Вы можете получить соответствующие компоненты этого представления, найдя модуль и комплексный аргумент комплексного числа. В R вы должны использовать Mod и Arg:

z <- complex(real = , imaginary = 1)
Mod(z)
# [1] 1
Arg(z)
# [1] 1.570796
pi / 2
# [1] 1.570796

Это соответствует интуиции, что i должен находиться на расстоянии 1 от начала координат и под углом пи/2.

Наконец, вы можете получить комплексное сопряжение комплексного числа, для этого в R вы можете использовать Conj:

Conj(z)
# [1] 0-1i
Mod(z) == z * Conj(z)
# [1] TRUE

Как видите, модуль z равен z, умноженному на сопряжение z, и это именно то, что вы ожидаете.

Исторически сложилось так, что комплексные числа были изобретены для того, чтобы можно было найти квадратный корень из отрицательных чисел. По умолчанию sqrt не возвращает комплексное число, когда вы запрашиваете квадратный корень из отрицательного числа. Вместо этого он выдает ошибку NaN, как вы можете видеть ниже:

sqrt(-1)
# [1] NaN
# Warning message:
# In sqrt(-1) : NaNs produced

Чтобы получить комплексный квадратный корень, вам нужно преобразовать отрицательное число в комплексное число с помощью as.complex перед применением sqrt:

sqrt(as.complex(-1))
# [1] 0+1i

На практике комплексные числа можно использовать для решения огромного круга задач, не последней из которых является эффективное представление БПФ входного вектора. Ради интереса я подумал, что покажу простое приложение: построение фрактала с помощью множества Мандельброта.

Цитата из Википедии:

Математически множество Мандельброта можно определить как набор комплексных значений c, для которых орбита 0 при итерации комплексного квадратичного многочлена z_n+1 = z_n^2 + c остается ограниченной. То есть комплексное число c находится в множестве Мандельброта, если при запуске с z = 0 и многократном применении итерации абсолютное значение z_n никогда не превышает определенного числа (это число зависит от c), каким бы большим ни было n.

Мы можем довольно легко перевести это определение в R, сделав определенные предположения о точности, которую мы хотим получить в наших результатах. Для моих целей я скажу, что число входит в множество Мандельброта, если после 100 итераций алгоритма Мандельброта оно ни разу не имело модуля больше 1000000. Как вы увидите из изображения, которое я создал, это предположение работает довольно хорошо, хотя для получения результатов для наборов данных разумного размера требуется некоторое вычисление реальных чисел.

in.mandelbrot.set <- function(c, iterations = 100, bound = 1000000) {
    z <- 0
    for (i in 1:iterations) {
        z <- z ** 2 + c
        if (Mod(z) > bound)
        {
            return(FALSE)
        }
    }
    return(TRUE)
}

Когда у нас есть этот алгоритм, мы можем легко сгенерировать изображение множества Мандельброта, создав матрицу комплексных чисел и изобразив их включение в набор с помощью изображения:

resolution <- 0.001
sequence <- seq(-1, 1, by = resolution)
m <- matrix(nrow = length(sequence), ncol = length(sequence))
for (x in sequence) {
    for (y in sequence) {
        mandelbrot <- in.mandelbrot.set(complex(real = x, imaginary = y))
        m[round((x + resolution + 1) / resolution), round((y + resolution + 1) / resolution)] <- mandelbrot
    }
}
png('mandelbrot.png')
image(m)
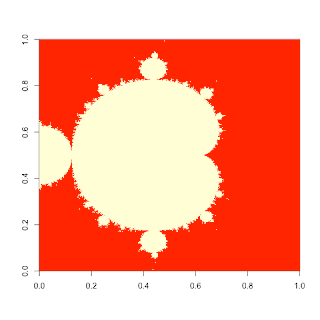
dev.off()

А вот получившееся изображение:

Оригинал: Using Complex Numbers in R