Жидкости везде. От океанских течений и потока воды в трубах до воздуха вокруг крыльев самолета и крови в наших венах - жидкости играют первостепенную роль в нашем мире. Область физики, изучающая эти явления, называется механикой жидкости, или гидромеханикой, и ее жемчужиной, несомненно, являются уравнения Навье-Стокса. Но какова именно интуиция, лежащая в основе уравнений Навье-Стокса и почему они так важны?
Введение
Грубо говоря, уравнения Навье-Стокса - это набор уравнений, которые могут описывать поток любой жидкости, о которой вы можете подумать.
Но прежде чем мы начнем распутывать эти уравнения, давайте напомним себе некоторые определения и концепции, которые помогут нам в дальнейшем.
Прежде всего, что такое жидкость?
Жидкость - это вещество, не имеющее фиксированной формы и легко поддающееся внешнему давлению. Когда такое давление - или напряжение, как это часто формально называется, применяется к жидкости, она претерпевает непрерывное изменение формы, поскольку положение некоторых из ее частиц изменяется относительно остальных. Это необратимое изменение известно как поток.
В этом контексте мы определяем вязкость жидкости как меру сопротивления жидкости потоку. Например, такие жидкости, как мед и кетчуп, имеют более высокую вязкость, чем вода и масло, которые являются очень жидкими веществами и имеют тенденцию легко течь. Вязкость - ключевое свойство любой жидкости, которое почти всегда проявляется в физике, лежащей в основе, которую мы используем для их моделирования.
От низкой до высокой вязкости слева направо
Есть два вида потоков, которые нас больше всего интересуют. Ламинарный и турбулентный поток.
Ламинарный поток - это «плавный» поток жидкости, тип потока, в котором движущиеся частицы остаются ограниченными в отдельных слоях. Эти слои плавно перемещаются мимо соседних слоев с небольшим перемешиванием или без него, как игральные карты.
Ламинарное течение в трубе
Турбулентный поток противоположен этому. Это тип потока, характеризующийся вихрями и множеством хаотических изменений давления и скорости жидкости в целом.
Турбулентное течение в трубе
Для простоты мы сделаем два ключевых предположения в оставшейся части этой статьи. Жидкости, с которыми мы будем иметь дело, являются ньютоновскими, то есть их вязкость остается постоянной независимо от величины сдвига - давления, приложенного к ним, и несжимаемыми, то есть их плотность остается постоянной во время течения.
Это почти все, что нам нужно знать. Теперь мы готовы погрузиться в элегантность уравнений Навье-Стокса!
Уравнения Навье-Стокса
Без лишних слов, вот два уравнения.
где:
u: вектор скорости жидкости
p: давление жидкости
ρ: плотность жидкости
μ: вязкость жидкости
∇²: оператор Лапласа (сумма трех пространственных производных второго порядка векторного поля, над которым он действует)
Как мы видим, оба уравнения относятся к u, вектору скорости жидкости. Проще говоря, векторное поле - это то, что мы получаем, когда назначаем каждую точку пространства вектору, стрелке с величиной и направлением. Векторные поля можно использовать для описания многих вещей, но в нашем примере каждый вектор представляет скорость жидкости в этой конкретной точке.
Пример векторного поля
Мы рассмотрим оба уравнения Навье-Стокса отдельно, начиная с меньшего.
Сохранение массы
Первое из двух приведенных выше уравнений является математическим выражением сохранения массы.
Как мы знаем, дивергенция векторного поля в определенной точке является мерой того, насколько векторное поле имеет тенденцию «расширяться» или расходиться в этой точке. Точки с положительной дивергенцией можно рассматривать как «источники», поскольку кажется, что жидкость возникает из ничего. С другой стороны, точки с отрицательной дивергенцией, как правило, рассматриваются как «стоки», где жидкость, кажется, полностью исчезает в ничто.
Источники и стоки векторного поля
Если вы поняли все это, первое из уравнений Навье-Стокса к настоящему времени должно быть довольно простым. Для реальной (несжимаемой) жидкости поле вектора скорости должно везде иметь нулевую дивергенцию. Если дивергенция не равна нулю, это означает, что в определенных точках жидкость либо сжимается, либо расширяется (создавая ненулевую производную от ее плотности по времени), что по предположению невозможно.
И это все! Перейдем ко второму уравнению.
Сохранение импульса
По общему признанию, второе уравнение при первом просмотре выглядит немного устрашающе. Давайте разберемся по порядку.
Прежде всего, это уравнение - не что иное, как применение второго закона Ньютона для жидкостей.
Второй закон Ньютона
Левая сторона - масса, умноженная на ускорение
Левая часть уравнения Навье-Стокса может быть переписана следующим образом:
Теперь сравнение со вторым законом Ньютона становится более очевидным. Вместо массы, мы использовали плотность жидкости (они математически взаимозаменяемы, когда объем постоянный), и мы записали ускорение как производную от скорости. Чтобы быть более конкретным, это на самом деле называется материальной производной, которую можно записать следующим образом, используя правило цепи:
Мы не будем говорить о том, что представляет собой материальная производная, но вы легко можете найти множество ресурсов в Интернете.
Правая часть - сумма сил.
Правая часть второго уравнения Навье-Стокса представляет собой алгебраическую сумму всех сил, действующих на жидкость. Мы не будем здесь формально выводить уравнение, поскольку оно не способствует нашему пониманию, хотя вы можете найти его в Интернете.
Мы можем различать внутренние и внешние силы.
∇p: первая внутренняя сила, которую мы принимаем во внимание, это давление. Этот термин представляет собой градиент давления, и он в основном представляет собой разницу давлений в пространстве, где находится жидкость. Точно так же, как когда мы всасываем воздух из соломинки, чтобы позволить соку достичь нашего рта, жидкости имеют тенденцию перемещаться из зон с более высоким давлением в зоны с более низким давлением. Эта тенденция заключена в этом термине - градиент давления.
μ∇²u: вторая внутренняя сила, которую мы учитываем, это трение, связанное с вязкостью жидкости. Между молекулами жидкостей с высокой вязкостью трение больше, чем между молекулами с низкой. Этот термин позволяет нам выразить это понятие в компактной математической форме.
ρf: Наконец, этот член учитывает все потенциальные внешние силы, которые могут действовать на жидкость. В большинстве случаев гравитация является единственной внешней силой в нашей системе, поэтому мы заменяем «f» на g, получая произведение ρg. В других случаях мы можем по-настоящему фантазировать и заменить ρf на силу Лоренца, комбинируя уравнения Навье-Стокса с уравнениями Максвелла.
Число Рейнольдса
Это число часто идет рука об руку с уравнениями Навье-Стокса. Число Рейнольдса, называемое Re, используется для определения того, является ли поток жидкости ламинарным или турбулентным.
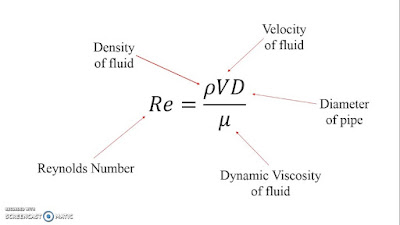
Формула для числа Рейнольдса следующая:
Число Рейнольдса в трубе
Обратите внимание, что D называется характеристической длиной, и она будет зависеть от типа анализируемого потока. На изображении выше мы предположили, что поток происходит внутри трубы, и поэтому D равен диаметру этой трубы.
Простыми словами, число Рейнольдса - это отношение сил инерции к силам вязкости. Если силы инерции - силы, которые заставляют жидкость двигаться, намного больше, чем силы вязкости - силы, противоположные потоку жидкости, тогда поток будет турбулентным. Если вместо этого преобладают вязкие силы, течение будет ламинарным. Но что именно означает «намного больше»?
Что ж, для чисел Рейнольдса в трубе меньше 2000 поток обычно будет ламинарным. Для Re больше 4000 поток будет турбулентным, в то время как для Re между 2000 и 4000 будет существовать своего рода переходный поток, гибрид между ламинарным и турбулентным потоками.
Миллион долларов ждет
Инженеры и физики широко используют уравнения Навье-Стокса во многих реальных приложениях. Однако, чтобы использовать эти уравнения, они почти всегда делают определенные допущения и упрощения в зависимости от решаемой задачи.
Причина, по которой они это делают, заключается в том, что эти уравнения чрезвычайно трудно решить в их первоначальной форме без каких-либо приближений. Фактически, Институт математики Клэя назначил награду в миллион долларов тому, кто сумеет решить эту задачу. Проще говоря (вы можете увидеть официальную постановку проблемы здесь), вам нужно ответить на следующий вопрос, чтобы получить миллион долларов:
Можете ли вы определить, существует ли гладкое решение для жидкостей в трех измерениях в каждой точке пространства?
Заключительные замечания
Уравнения Навье-Стокса входят в число наиболее важных и широко применяемых уравнений во всей физике. Они помогают нам проектировать самолеты и автомобили, изучать кровоток, проектировать электростанции, анализировать загрязнение окружающей среды и многое другое. Однако из-за присущей им математической сложности их можно решить только с помощью приближений, в то время как теоретическое доказательство гладкого решения будет вознаграждено одним миллионом долларов.
«Когда я встречусь с Богом, я задам ему два вопроса: Почему относительность? А почему турбулентность? Я действительно верю, что он ответит на первый вопрос».
Вернер Гейзенберг на смертном одре












Комментариев нет:
Отправить комментарий