Введение
Каждый специалист по анализу данных должен создавать предметные знания в каждой области, потому что мы должны решать каждую проблему, с которой, вероятно, сталкивается мир. Если вы не знаете, что такое знание предметной области? это знание определенной области или специализация в какой-либо области. мы также можем сказать, что это часть общих знаний, поэтому, как специалисты по данным, мы, вероятно, решаем реальные проблемы, которые были основаны на машинном обучении, со знанием предметной области конкретной проблемы.
Как специалисты по обработке данных, мы обычно сталкивались с множеством реальных проблем, таких как социальные проблемы, строительство и т. д. Мы должны решать этот тип проблем с помощью методов машинного обучения. Мы знаем, что качество является наиболее важным свойством материала, используемого в строительстве. Если качество бетона ниже, чем требуется, то постройка не может быть стабильной, но если мы используем бетон самого высокого качества, то здание будет стабильным и долговечным.
Чтобы узнать, является ли данный бетон качественным или нет, мы обычно проверяем прочность бетона. Проще говоря, прочность бетона на сжатие определяет качество бетона, мы проверяем его стандартным испытанием на раздавливание бетонного цилиндра. Прочность бетона также считается ключевым фактором в достижении желаемой прочности конструкции. На проверку прочности уйдет 28 дней, это большое время, так как мы может его сократить? Используя Data Science, мы сокращаем эти временные затраты и прогнозируем, какое сырье, и в каком количестве мы должны использовать для обеспечения хорошей прочности на сжатие.
Итак, мы собираемся проанализировать набор данных Concrete Compressive Strength и построить модель машинного обучения для прогнозирования качества:
Набор данных
Мы будем использовать набор данных прочности на сжатие бетона, который был получен из Kaggle, вы можете кликнуть здесь, чтобы получить его.
Описание набора данных
Если вы загрузите этот набор данных, вы увидите, что несколько признаков влияют на качество бетона. Итак, мы обсуждаем краткое описание каждого признака:
cement: вещество, используемое в строительстве, которое затвердевает при смешивании с водой.
slag: смесь оксидов металлов и диоксида кремния.
Flyash: продукт сгорания угля, состоящий из твердых частиц, которые выбрасываются из угольных котлов вместе с дымом.
Water: используется для получения бетонного раствора.
Superplasticizer: используется при изготовлении высокопрочного бетона.
Coaseseaggregate: щебень, полученный из наземных отложений.
fineaggregate: щебень с размером частиц менее 4,75 мм.
age: скорость набора прочности выше в начале, и она уменьшается с возрастом образца.
csMPa: единица измерения прочности бетона.
Теперь мы импортируем некоторые важные модули:
Импорт модулей
Для дальнейшего процесса нам нужно импортировать некоторые важные модули, присутствующие в python:
# importing pandas import pandas as pd #importing numpy import numpy as np #importing matplotlib import matplotlib.pyplot as plt #importing seaborn import seaborn as sb
Итак, мы импортируем pandas для анализа данных, NumPy для вычисления N-мерного массива, seaborn и matplotlib для визуализации данных.
Чтение данных
Как правило, мы используем набор данных в виде файла CSV, для чтения этого файла мы будем использовать библиотеку pandas, давайте посмотрим:
df = pd.read_csv(' Concrete_data.csv ')
dfИзучение набора данных
После чтения набора данных мы должны извлечь информацию из данных, для этого мы используем следующую функцию:
df.info()
Здесь мы отмечаем присутствие нулевых значений в каждом признаков и видим, какой тип данных признаков присутствует в наборе данных.
df.describe()
Метод description() производит различные вычисления для каждой точки данных в признаке.
Обработка нулевых значений
Теперь мы обрабатываем нулевые значения, которые присутствуют в наборе данных, для большей точности,
df.isnull().sum()
вы можете видеть, что в каждом признаке присутствует определенное количество нулевых значений, поэтому мы должны вменять им какое-то другое значение, чтобы заполнить нулевые значения,
num= df.select_dtypes(include=['int64','float64']).keys() from sklearn.impute import SimpleImputer impute=SimpleImputer(strategy='mean') impute_fit= impute.fit(df[num]) df[num]= impute_fit.transform(df[num]) df
Здесь мы используем метод преобразования, который известен как SimpleImputer, он используется для заполнения нулевых значений средними, медианными значениями и модами.
Исследовательский анализ данных (EDA)
EDA - важный шаг для создания любого проекта машинного обучения, это подход к анализу наборов данных для обобщения их основных характеристик. С помощью EDA мы можем получать информацию о признаках, просто наблюдая за графиками.
Итак, здесь мы будем использовать некоторые часто используемые методы визуализации для наблюдения за данными:
Парный график:
Он строит попарные соотношения в наборе данных, создает сетку осей, где ось Y принадлежит строке, а ось X - столбцам.
# pairplot of dataframe sb.pairplot( df )
Как вы можете видеть, он отображает корреляции между каждым признаком.
График рассеяния
Этот график отображает отношения между любыми двумя наборами данных.
# scatter plot of Water and Cement
plt.figure(figsize=[17,9])
plt.scatter(y='csMPa',x='cement',edgecolors='red',data=df)
plt.ylabel('csMPa')
plt.xlabel('cement')Мы используем matplotlib для построения графика рассеяния, на этом изображении вы можете ясно видеть, что ось x содержит точки данных cement, значения которых могут варьироваться от 100 до 500, а ось y представляет зависимую переменную csMPa, где ее точки данных варьируются от 0 до 80.
По мере того, как мы увеличиваем количество цемента в бетоне, качество бетона также может повышаться, как показано на диаграмме рассеяния.
В соответствии с этим мы также можем построить взаимосвязь между любыми другими двумя признаками, содержащимися в наборе данных. Давайте построим диаграмму рассеяния между csMPa и flyash.
plt.figure(figsize=[17,9])
plt.scatter(y='csMPa',x='flyash',edgecolors='blue',data=df)
plt.ylabel('csMPa')
plt.xlabel('flyash')Теперь построим график корреляции:
График корреляции
График корреляции показывает коэффициент корреляции между переменными. Этот график содержит таблицу в виде корреляционной матрицы.
Теперь мы визуализируем корреляцию между переменными, построив график:
plt.figure(figsize=[17,8])
#ploting correlation plot
sb.heatmap(df.corr(),annot=True)
Мы используем библиотеку seaborn для построения графика корреляции между переменными, здесь вы видите, что между переменными существует взаимосвязь один к одному. Каждая переменная показывает связь с другой переменной.
Если мы возьмем наблюдения из тепловой карты, то обнаружим, что cement имеет сильную корреляцию с water.
Теперь мы рисуем выброс, который присутствует в наборе данных:
Ящик с усами
l=['cement','slag','flyash','water','superplasticizer','coarseaggregate','fineaggregate','age','csMPa']
for i in l:
sb.boxplot(x=df[i])]' ]
plt.show()Посмотрите на диаграмму boxplot, вы заметите, что черные точки присутствуют слева и справа от линий, эти точки являются более резкими, чем те, которые присутствуют в конкретном признаке.
Разделение зависимых и независимых переменных
Перед тем, как начать построение модели, мы должны разделить набор данных на две части.
Независимые переменные содержат список тех переменных, от которых зависит качество бетона.
Зависимая переменная - это та переменная, которая зависит от значений других переменных.
# independent variables x = df.drop(['csMPa'],axis=1) # dependent variables y = df['csMPa']
В этой программе x содержит список независимых переменных, а y содержит зависимую переменную, в этом случае:
1. Независимые переменные: cement, flyash, water, superplasticizer, coaseseaggregate, fineaggregate, age.
2. зависимая переменная - только csMPa
Разделение данных
Теперь мы используем модуль scikit-learn train_test_split, которая применяется для разделения обучающей и тестовой выборок.
# importing train_test_split from sklearn.model_selection import train_test_split xtrain,xtest,ytrain,ytest= train_test_split(x,y,test_size=0.3,random_state=42)
Масштабирование признаков
Мы делаем масштабирование данных для балансировки точек данных.
from sklearn.preprocessing import StandardScaler stand= StandardScaler() Fit = stand.fit(xtrain) xtrain_scl = Fit.transform(xtrain) xtest_scl = Fit.transform(xtest)
В этой программе сначала мы импортируем train_test_split из scikit-learn, затем создаем объект класса StandardScaler(), после создания объекта мы подгоняем обучающие данные в StandardScaler для масштабирования данных, а затем преобразуем обучающие и тестовые данные в массив.
Применение модели
Машинное обучение состоит из алгоритмов, которые могут автоматизировать построение аналитических моделей. Используются алгоритмы, которые итеративно учатся на данных. На этом этапе мы применяем несколько алгоритмов машинного обучения к обучающей выборке.
Давайте посмотрим ниже:
Линейная регрессия
# import linear regression models
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lr=LinearRegression()
fit=lr.fit(xtrain_scl,ytrain)
score = lr.score(xtest_scl,ytest)
print('predcted score is : {}'.formate(score))
print('..................................')
y_predict = lr.predict(xtest_scl)
print('mean_sqrd_error is ==',mean_squared_error(ytest,y_predict))
rms = np.sqrt(mean_squared_error(ytest,y_predict))
print('root mean squared error is == {}'.format(rms))Теперь мы строим диаграмму рассеяния и подгоняем прямую для проверки прогнозных значений:
plt.figure(figsize=[17,8])
plt.scatter(y_predict,ytest)
plt.plot([ytest.min(), ytest.max()], [ytest.min(), ytest.max()], color='red')
plt.xlabel('predicted')
plt.ylabel('orignal')
plt.show()Вы можете увидеть, что прямая частично соответствует нашим прогнозируемым точкам данных.
Лассо и гребневая регрессия
# import rigd and lasso regresion
from sklearn.linear_model import Ridge,Lasso
from sklearn.metrics import mean_squared_error
rd= Ridge(alpha=0.4)
ls= Lasso(alpha=0.3)
fit_rd=rd.fit(xtrain_scl,ytrain)
fit_ls = ls.fit(xtrain_scl,ytrain)
print('score od ridge regression is:-',rd.score(xtest_scl,ytest))
print('.......................................................')
print('score of lasso is:-',ls.score(xtest_scl,ytest))
print('mean_sqrd_roor of ridig is==',mean_squared_error(ytest,rd.predict(xtest_scl)))
print('mean_sqrd_roor of lasso is==',mean_squared_error(ytest,ls.predict(xtest_scl)))
print('root_mean_squared error of ridge is==',np.sqrt(mean_squared_error(ytest,rd.predict(xtest_scl))))
print('root_mean_squared error of lasso is==',np.sqrt(mean_squared_error(ytest,lr.predict(xtest_scl))))Этот алгоритм двух регрессий дает немного другую оценку прогноза по сравнению с линейной регрессией.
Теперь мы построим диаграмму рассеяния предсказанных данных и построим прямую.
График гребневой регрессии:
plt.figure(figsize=[17,8])
plt.scatter(y_predict,ytest)
plt.plot([ytest.min(), ytest.max()], [ytest.min(), ytest.max()], color='red')
plt.xlabel('predicted')
plt.ylabel('orignal')
plt.show()График регрессии лассо:
plt.figure(figsize=[17,8])
plt.scatter(y_predict,ytest)
plt.plot([ytest.min(), ytest.max()], [ytest.min(), ytest.max()], color='red')
plt.xlabel('predicted')
plt.ylabel('orignal')
plt.show()Мы можем видеть на этих двух графиках, что они очень похожи, потому что оценка прогноза или оба алгоритма немного похожи.
RandomForestRegressor
# import random forest regression
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
rnd= RandomForestRegressor(ccp_alpha=0.0)
fit_rnd= rnd.fit(xtrain_scl,ytrain)
print('score is:-',rnd.score(xtest_scl,ytest))
print('........................................')
print('mean_sqrd_error is==',mean_squared_error(ytest,rnd.predict(xtest_scl)))
print('root_mean_squared error of is==',np.sqrt(mean_squared_error(ytest,rnd.predict(xtest_scl))))Оценка точности RandomForestRegressor является самой высокой среди линейной регрессии, регрессии лассо и гребневой, поэтому мы используем модель RandomForestRegressor. Здесь самая высокая точность означает, что она лучше предсказывает качество бетона, а также дает меньшую частоту ошибок.
Прогнозируемые значения по сравнению с исходными значениями
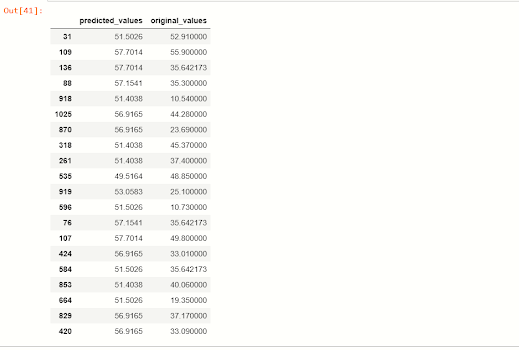
Теперь мы смотрим соответствие между предсказанными значениями зависимой переменной csMPa и исходными значениями.
x_predict = list(rnd.predict(xtest))
predicted_df = {'predicted_values': x_predict, 'original_values': ytest}
#creating new dataframe
pd.DataFrame(predicted_df).head(20)Вы можете видеть, что при применении модели RandomForestRegressor прогнозируемые значения очень похожи на наши исходные значения.
Сохранение модели
Теперь мы сохраняем нашу модель машинного обучения с помощью pickle.
import pickle file = 'concrete_strength' save = pickle.dump(rnd,open(file,'wb'))

















Комментариев нет:
Отправить комментарий